1. 서 론
말뚝의 축방향 허용지지력은 말뚝재료의 허용압축하중과 지반의 허용지지력 중 작은 값으로 결정한다. 국내의 경우 말뚝이 설치되는 지반의 허용지지력은 말뚝재료의 허용하중과 비교하여 작은 것이 보통이며 이에 따라 말뚝의 축방향 허용지지력은 지반의 허용지지력에 의하여 결정되는 경우가 대부분이다(KGS, 2015). 그러나 최근에는 말뚝의 시공 및 관리기술의 향상에 힘입어 말뚝재료의 허용하중에 상당하는 지반조건까지 말뚝을 시공하여 말뚝재료를 최대한 활용하는 설계방법도 적용되고 있으며 이러한 장대말뚝의 설계 시 말뚝의 좌굴 안정성에 대한 검토는 필수적이다. 이는 작용하중이 허용압축하중보다 작아 축방향 하중에 의한 압축파괴에 대해서는 안정하더라도 횡방향 굽힘에 따른 좌굴파괴가 발생할 수 있기 때문이다(AASHTO, 2012). 특히, 연약한 점토지반이나 액상화 및 세굴 발생 지반의 경우 좌굴에 의한 붕괴가능성은 증가한다(Shanker et al., 2007, Vogt et al., 2009, Jeong et al., 2015, Liang et al., 2015, Albusoda and Abbase, 2017).
그동안 축방향 압축하중을 받는 말뚝의 좌굴 거동에 관한 많은 연구가 수행되었다. Hetenyi(1946)에 의한 탄성기초 위에 놓인 보의 안정성에 대한 접근법은 탄성지반에 의해 횡방향으로 지지된 말뚝의 좌굴해석으로 확장되었다. 예로서, Bjerrum(1957)은 회전-회전 단부조건을 갖는 말뚝의 좌굴하중에 대한 정확해를 산정하였고 Davisson et al.(1963, 1965)은 부분매립 말뚝의 단부조건이 말뚝 거동에 미치는 영향을 연구하였다. Prakash(1987)와 Chen et al.(2015)은 말뚝의 좌굴하중을 산정에 있어서 에너지법과 첨단재앙이론(cusp catastrophe theory)를 각각 적용하였다. West et al.(1997)은 말뚝의 좌굴하중과 좌굴모드를 군집형태(clustering pattern)에 대하여 연구하였다. Vogt et al.(2009)은 모형실험을 통하여 지반의 비선형을 고려한 말뚝의 비탄성 좌굴거동을 평가하였고 Deng et al.(2017)은 Vlasov 지반에 설치된 말뚝의 좌굴하중을 산정하였다.
이상의 연구에서는 말뚝 축에 작용하는 축방향력은 일정하다고 가정하여 말뚝 축을 통한 축하중의 변화를 허용하지 않았다. 이러한 가정은 길이가 상대적으로 짧은 말뚝의 좌굴하중 산정에는 적합하지만, 대심도 말뚝에서는 축방향력의 변화를 고려하여야 한다. 이는 상부하중으로 인해 말뚝 주면에 발생하는 수직방향의 상향 저항력이 말뚝의 좌굴 거동에 영향을 미치기 때문이다. 지금까지 말뚝의 주면마찰력을 고려한 말뚝-지반 상호작용에 관한 연구는 매우 제한적이다. 그동안 마찰말뚝의 좌굴에 대한 연구는 에너지 법(Reddy and Valsangkar, 1970), Rayleigh-Ritz 법(Gabr et al., 1994) 및 모드군집 법(modal clustering technique, Heelis et al., 2004) 등의 다양한 방법이 적용되었지만 이들은 모두 원통형 말뚝을 대상으로 하였다.
이 논문은 비균질 지반에 시공된 테이퍼 마찰말뚝의 좌굴 거동을 연구하는 데 그 목적이 있다. 이를 위해 말뚝의 변단면, 지반의 비균질성, 말뚝의 주면마찰의 영향을 고려하여 지반-말뚝 시스템의 좌굴을 지배하는 상미분방정식과 경계조건을 유도하였다. 원통형 마찰말뚝에 대한 좌굴하중의 수치해를 문헌값(Gabr et al., 1994)과 비교하여 제안된 해석모델의 타당성을 검증하고, 지반-말뚝에 관련된 무차원변수가 좌굴하중 및 좌굴모드, 좌굴응력에 미치는 영향을 분석하였다.
2. 지반-말뚝 시스템
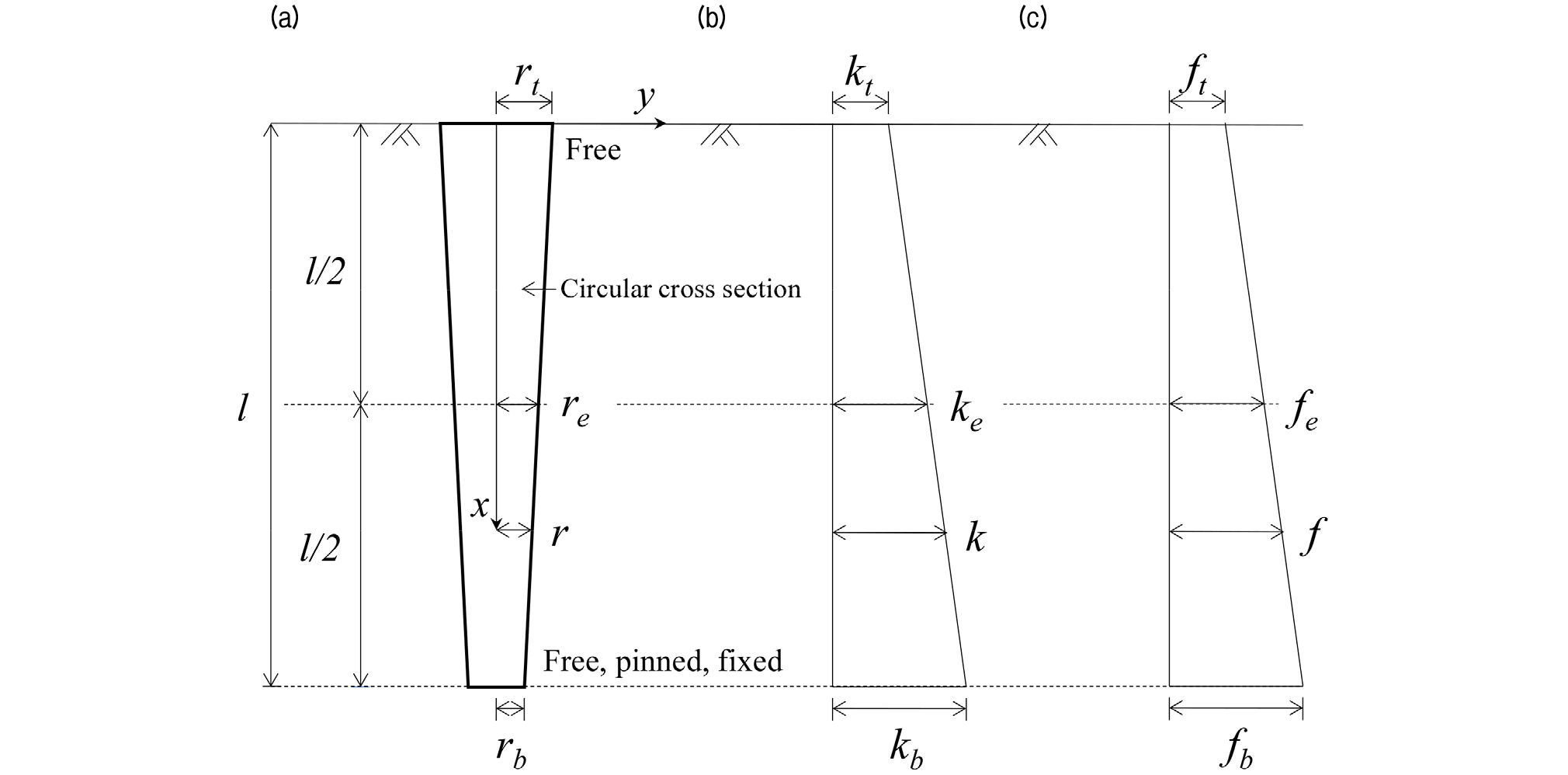
Fig. 1은 비균질 지반에 매설된 테이퍼 마찰말뚝의 좌굴해석에 필요한 변수들을 나타낸다. Fig. 1(a)와 같이 말뚝길이는 l이며 말뚝단면은 원형으로 가정한다. 테이퍼 말뚝의 단면은 깊이가 증가함에 따라 선형으로 감소한다. 말뚝두부 x = 0의 반경은 rt이고 말뚝선단 x = l에서는 rb이다. 말뚝 깊이 x에서의 반경 r을 수식화하기 위하여 단면비 ar를 다음과 같이 정의한다.
| $$a_r=\frac{r_b}{r_t}$$ | (1) |
본 연구의 단면비 ar는 0과 1사이에 존재하며, 이는 말뚝의 단면이 깊이 방향으로 작아지는 형태의 테이퍼 말뚝을 의미한다. 한편, 말뚝 중앙에서의 반경 re는 다음과 같이 표현할 수 있다.
| $$r_e=\frac12(r_t+r_b)$$ | (2) |
이로부터 말뚝 중앙에서의 단면폭 we, 원주길이 ue, 단면적 Ae, 단면이차모멘트 Ie는 다음과 같이 구할 수 있다.
| $$w_e=2r_e,\;u_e=2\pi r_e,\;A_e=\pi r_e^2,\;I_e=\pi r_e^4/4$$ | (3) |
식 (1), (2)를 이용하면 말뚝 깊이 x에서의 반경 r을 다음과 같이 표현할 수 있다.
| $$r=\frac{2r_e}{m_r}H_x$$ | (4) |
여기서 mr=ar+1, nr=ar-1, Hx=1+nr(x/l)이다.
한편, 말뚝 깊이 x에서의 단면폭 w, 원주길이 u, 단면적 A, 단면이차모멘트 I는 반경 r의 함수로 이를 정리하면 다음과 같다.
| $$W=\frac{4r_e}{m_r}H_x,\;A=\frac{4\pi r_e^2}{m_r^2}H_x^2,\;I=\frac{4\pi r_e^4}{m_r^4}H_x^4$$ | (5) |
Fig. 1(b)는 지반의 비균질성을 나타나며 이는 말뚝 깊이에 따라 선형적으로 증가하는 지반반력계수(coefficient of subgrade reaction)로 고려된다. 말뚝의 두부와 선단에서 지반반력계수는 각각 kt와 kb이다. 말뚝 깊이 x에서의 지반반력계수 k를 수식화하기 위하여 지반반력계수비 ak를 다음과 같이 정의한다.
| $$a_k=\frac{k_b}{k_t}$$ | (6) |
여기서, ak < 1와 ak > 1는 깊이 방향에 따른 지반반력의 감소와 증가를 각각 의미하고 ak = 1은 깊이 방향에 따른 지반반력이 일정한 균일한 지반을 나타낸다.
말뚝 중앙과 말뚝 깊이 x에서의 지반반력계수 ke, k는 다음과 같이 표현할 수 있다.
| $$k_e=\frac12(k_t+k_b)$$ | (7) |
| $$k=\frac{2k_e}{m_k}Q_x$$ | (8) |
여기서 mk=ak+1, nk=ak-1, Qx=1+nk(x/l)이다.
Fig. 1(c)는 축방향 압축하중을 받는 테이퍼 말뚝의 주면에 발생하는 단위주면마찰력(unit side-friction resistance)을 나타내며 이는 말뚝 깊이에 따라 선형적으로 증가한다. 말뚝의 두부와 선단에서의 단위주면마찰력은 각각 ft와 fb이다. 말뚝 깊이 x에서 단위주면마찰력 f를 수식화하기 위하여 주면마찰계수비 af를 다음과 같이 정의한다.
| $$a_f=\frac{f_b}{f_t}$$ | (9) |
본 연구에서 주면마찰계수비는 af ≥ 1의 값을 가지며 이는 단위주면마찰력이 깊이 방향으로 일정하거나 선형적으로 증가하는 지반을 의미한다. 한편, 말뚝 중앙과 말뚝 깊이 x에서의 단위주면마찰력 f를 각각 다음과 같이 구할 수 있다.
| $$f_e=\frac12(f_t+f_b)$$ | (10) |
| $$f=\frac{2f_e}{m_f}S_x$$ | (11) |
여기서 mf=af+1, nf=af-1, Sx=1+nf(x/l)이다.
한편, 테이퍼 말뚝의 경계조건으로 말뚝두부는 자유, 말뚝선단은 자유, 회전, 고정으로 가정한다. 즉, Fig. 1(a)와 같이 말뚝의 경계조건은 자유-자유, 자유-회전 및 자유-고정을 적용한다.
3. 수학적 정식화
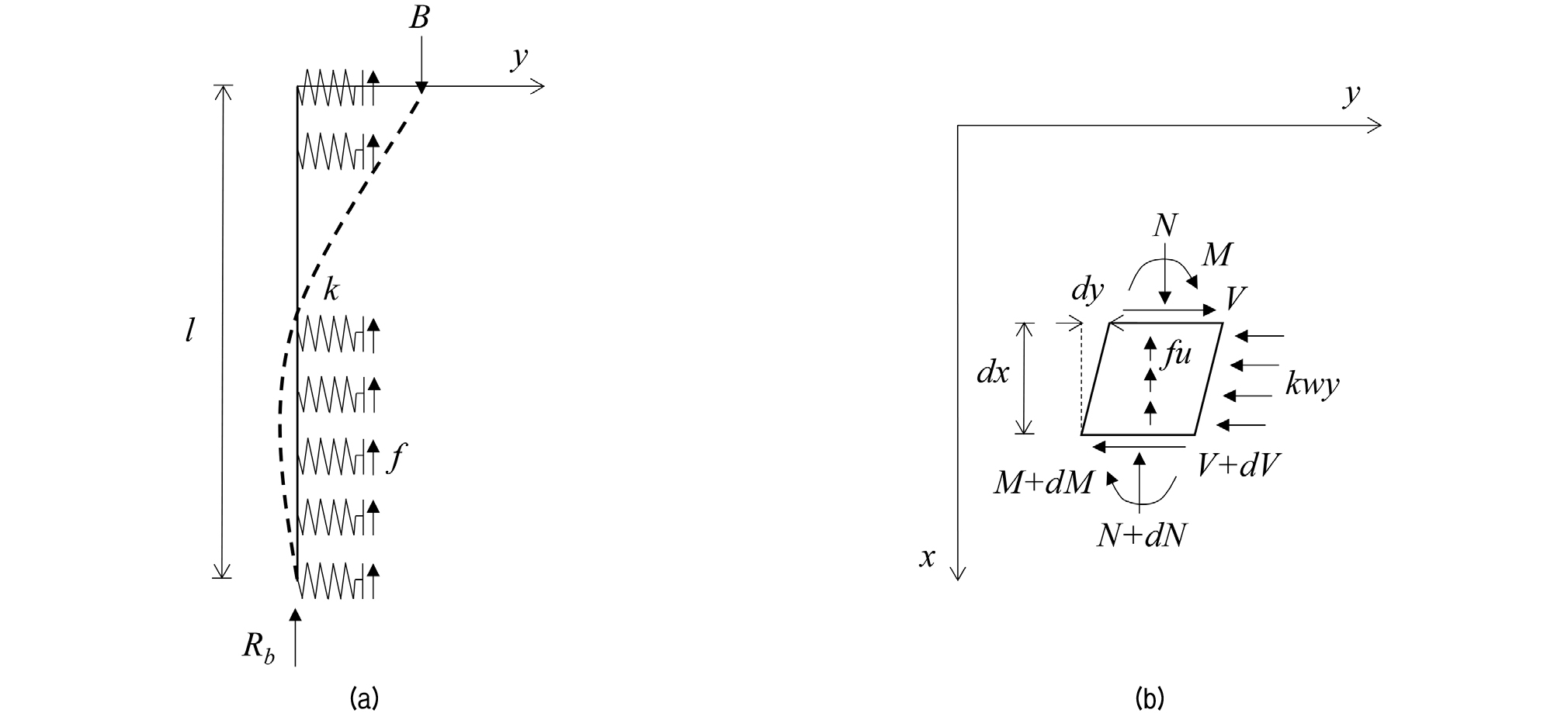
Fig. 2(a)는 말뚝두부에 가해진 좌굴하중 B에 의해 변형된 말뚝형상의 예를 직교좌표계 (x, y)에 나타낸 그림이다. 이 때, 말뚝선단에는 상향 반력 Rb가 작용하고 말뚝 내부에는 축방향력 N, 전단력 V, 휨 모멘트 M의 합응력이 작용한다. 말뚝 외부에는 말뚝변위 y에 저항하여 y의 반대방향으로 수평방향 지반반력 kwy가 발생하고 축방향력 N에 의하여 주면마찰력 fu가 상향으로 작용한다.
Fig. 2(b)는 미소길이 dx를 갖는 말뚝요소의 자유물체도를 직교좌표계 (x, y)에 나타낸 것이다. 이 요소에는 내력인 합응력 N, V, M과 외력인 지반반력 kwy 및 마찰력 fu가 작용하여 평형상태를 이룬다. 따라서 ∑Fx=0, ∑Fy=0, ∑M=0의 평형방정식을 구하면 다음 식들과 같다.
| $$\frac{dN}{dx}+fu=0$$ | (12) |
| $$\frac{dV}{dx}+kwy=0$$ | (13) |
| $$\frac{dM}{dx}-V+N\frac{\displaystyle dy}{\displaystyle dx}=0$$ | (14) |
말뚝요소에 대한 다음의 휨-변위 관계식(Gere and Timoshenko, 1997),
| $$M=EI\frac{d^2y}{dx^2}$$ | (15) |
를 식 (12)-(14)와 조합하여 풀면 다음과 같은 4계 미분방정식을 얻는다.
여기서 E는 말뚝의 탄성계수이고, 말뚝 깊이 x에서의 축방향력 N은 다음과 같이 정의할 수 있다.
| $$N=B-\int_0^xfu\;dx$$ | (17) |
위의 식 (17)에 식 (5), (11)을 대입하여 정리하면 다음과 같다.
| $$N=B-\frac{8\pi r_ef_el}{m_rm_f}T_x$$ | (18) |
여기서 이며, 깊이 x = l에서의 축방향력 Nx=l은 Rb와 동일하다.
해석의 편의를 위해 다음과 같은 무차원 변수를 도입한다.
| $$\xi=\frac xl,\;\eta=\frac yl,\;\gamma=\frac{\omega_e}l,\;\alpha=\frac l\lambda,\;\beta=\frac{f_eu_e\lambda^3}{\pi EI_e},\;b=\frac{Bl^2}{\pi^2EI_e}$$ | (19) |
여기서, ξ와 η는 무차원 직교좌표, γ는 장경비, α는 특성길이비, β는 마찰변수, b는 좌굴하중변수이다. 식 (19)에서 λ는 다음 식 (20)으로 정의되는 특성길이(characteristic length)이며 지반-말뚝의 상대강성을 의미한다.
| $$\lambda=\sqrt[5]{\frac{EI_e}{k_e}}$$ | (20) |
식 (19), (20)을 식 (16)에 대입하고, 이미 유도해 놓은 식 (5), (8), (11), (18)을 이용하여 정리하면 다음과 같은 무차원 4계 상미분방정식을 얻을 수 있다.
여기서 , , , 이다.
이제, 지배 미분방정식의 경계조건을 다음과 같이 유도한다. 말뚝두부는 자유이므로 x = 0에서 휨 모멘트 M과 전단력 V는 0이다. 이로부터 ξ = 0에서 자유단의 경계조건을 다음과 같이 구할 수 있다.
| $$\frac{d^2\eta}{d\xi^2}=0;\;\;\frac{\displaystyle d^3\eta}{\displaystyle d\xi^3}+\frac{\pi^2m_r^4b}{16}\frac{\displaystyle d\eta}{\displaystyle d\xi}=0$$ | (22) |
유사하게 말뚝선단(x = l)이 자유단인 경우, ξ = 1에서의 경계조건은 다음과 같다.
말뚝선단이 회전단인 경우, 수평변위 y와 휨 모멘트 M은 0이므로 ξ = 1에서의 경계조건은 다음과 같다.
| $$\eta=0;\;\;\frac{d^2\eta}{d\xi^2}=0$$ | (24) |
말뚝선단이 고정단인 경우, 수평변위 y와 회전각 dy/dx는 0이므로 ξ = 1에서의 경계조건은 다음과 같다.
| $$\eta=0;\;\;\frac{d\eta}{d\xi}=0$$ | (25) |
이상과 같이 본 연구의 말뚝 단부조건은 자유-자유, 자유-회전, 자유-고정을 적용하였으나 유사한 방법으로 그 밖의 단부조건을 유도할 수 있다.
말뚝에 좌굴하중 B가 작용하면 말뚝 깊이 x에는 축방향력 N에 의한 좌굴응력 σb가 발생한다. 이 좌굴응력 σb는 식 (5), (18)로 수식화된 A, N식을 이용하여 다음과 같이 무차원화할 수 있다.
| $$\zeta_b=\frac{\pi^2\sigma_b}E=\frac{\pi^2N}{EA}=\frac{\pi^4m_r^2\gamma^2}{64h_\xi^2}\left(b-\frac{4\alpha^3\beta}{\pi m_rm_f}t_\xi\right)$$ | (26) |
여기서 ζb는 좌굴응력변수이다.
4. 수치방법 및 검증
이상에서 비균질 지반 속에 매설된 테이퍼 말뚝의 좌굴해석을 위한 지배방정식 (21)과 경계조건식 (22)-(25)를 유도하였다. 수치해석을 위한 입력변수는 말뚝의 단부조건과 더불어 단면비 ar, 지반반력계수비 ak, 주면마찰계수비 af, 장경비 γ, 특성길이비 α, 마찰변수 β이고, 입력변수에 의해 계산되는 상수들은 mr=ar+1, nr=ar-1, mk=ak+1, nk=ak-1, mf=af+1, nf=af-1이다. 수치해석을 통해 얻는 결과값은 좌굴하중변수 b, 좌굴모드 (ξ, η), 좌굴응력변수 ζb이다. 미분방정식의 고유치인 좌굴하중변수 b는 비선형방정식의 해법 중에 하나인 Regula-Falsi 법을 이용하였고 좌굴모드 (ξ, η)은 Runge-Kutta 법을 이용한 수치적분을 통해 산정하였다(Carnahan et al., 1969). 좌굴응력변수 ζb는 입력변수와 결과값을 식 (26)에 대입하여 계산할 수 있다. 이와 같은 지반-기초 시스템의 고유치 문제에 대한 구체적인 수치해석 방법은 기존 문헌(Lee et al., 2014)에서 찾을 수 있다.
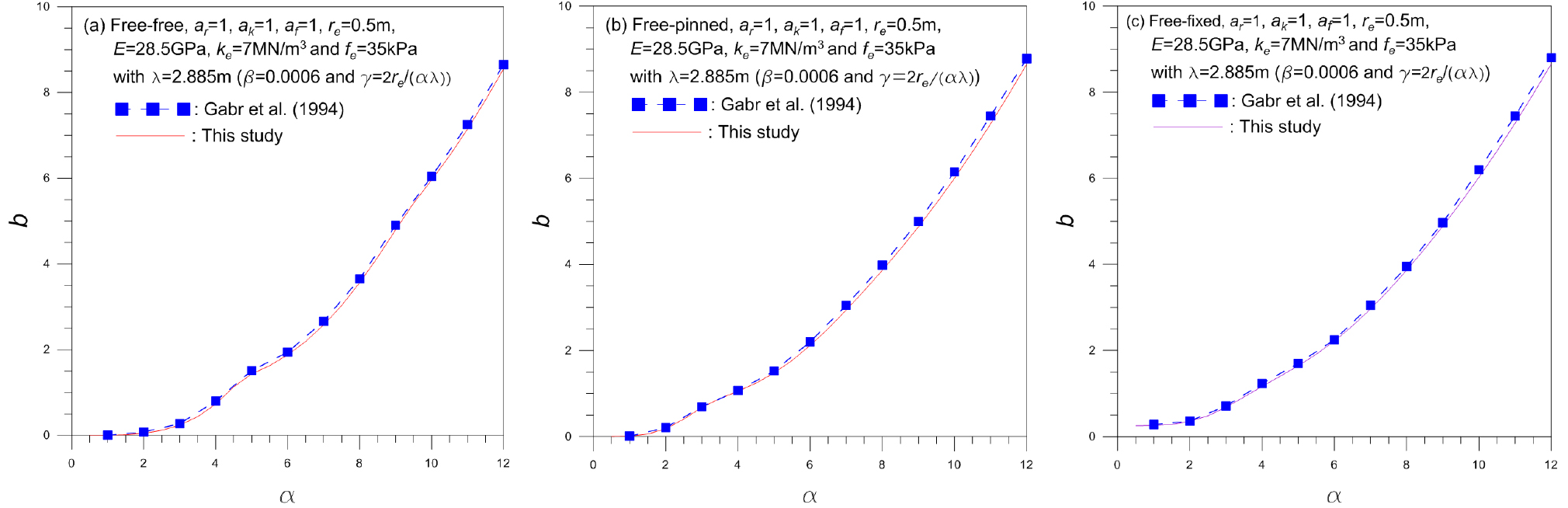
Fig. 3은 원통형 마찰말뚝에 대한 좌굴하중변수 b를 나타낸 그림이며 수치해 산정에 이용한 경계조건과 입력변수를 그림 상단에 나타내었다. 해석모델의 검증을 위해 결과값과 Gabr et al.(1994)의 값을 함께 나타냈었고 이로부터 두 결과값이 우수하게 근접하는 것을 확인할 수 있다. 참고로 Gabr et al.(1994)의 값은 경계조건을 만족하는 수식으로 좌굴모드를 가정하여 미분방정식에 대입하는 Rayleigh-Ritz 법을 이용하여 얻은 결과이고 본 해석결과는 미분방정식을 직접 적분하여 얻은 결과로 수치해석방법에 차이가 있음을 밝혀둔다.
5. 수치결과 및 토의
지반-말뚝 시스템의 재료 및 기하학적 특성이 좌굴하중에 미치는 영향을 분석하기 위하여 다음과 같은 입력변수를 적용하여 수치해석하였다: re=0.5m, ke=10MN/m3, E=20GPa. 이들 값에 대한 특성길이는 λ=2.5m로 계산되며 이 경우 γα=0.4로 장경비 γ와 특성길이비 α는 서로 종속적인 관계를 갖는다. 그 밖에 해석에 사용된 무차원 변수는 Figs. 4-8의 상단에 표시되어 있다.
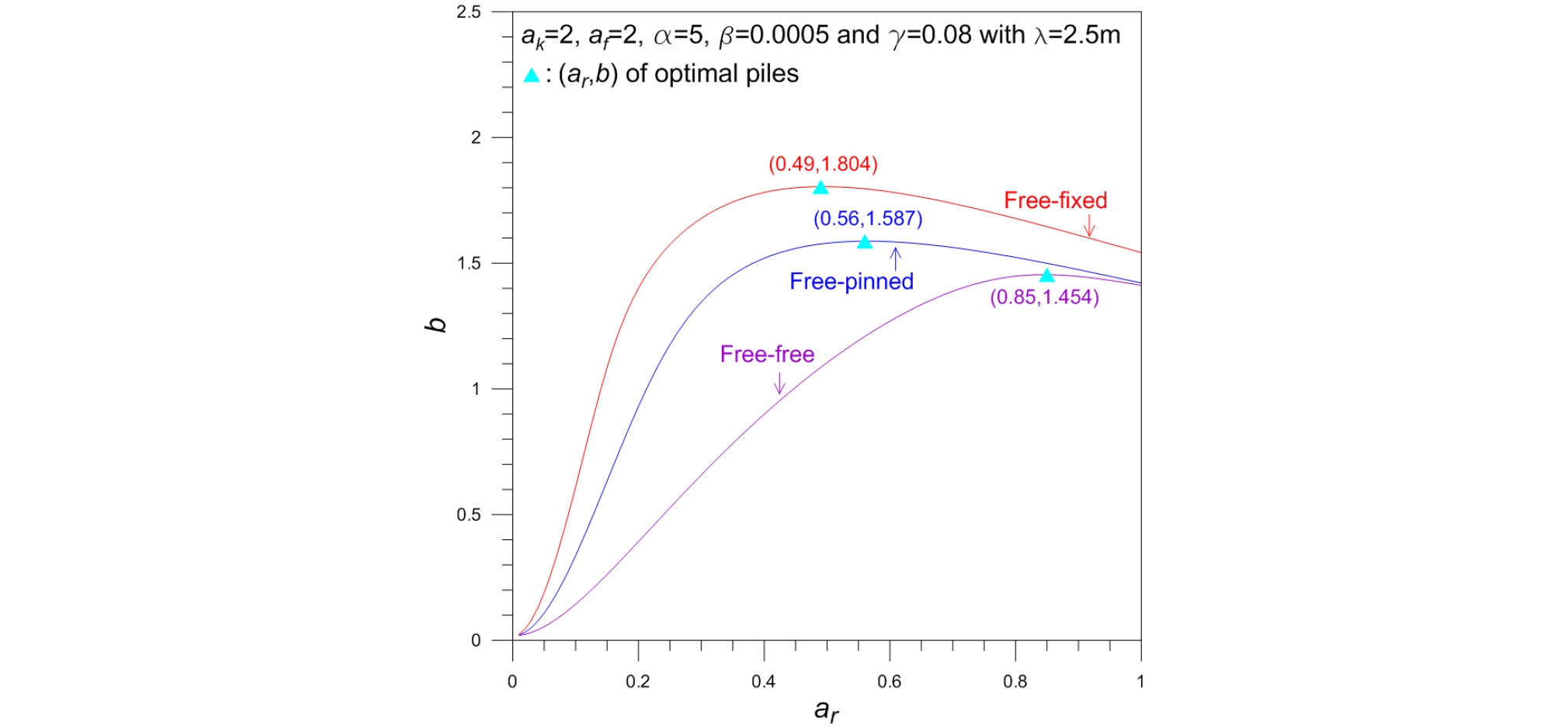
Fig. 4는 깊이 방향으로 단면이 작아지는 테이퍼 말뚝의 좌굴하중변수 b에 대한 단면비 ar의 영향을 나타낸다. 주어진 말뚝-지반조건에서 ar이 증가하면 b는 증가하다가 ▲로 표시한 좌표에서 최대치를 보인 후에 다시 감소한다. 이 그림에서 ▲는 다른 변수가 일정할 때 가장 큰 좌굴하중 b를 갖는 단면비 ar를 나타내며 이 때의 말뚝을 최적말뚝이라 표현할 수 있다. 예로서 자유-고정 말뚝인 경우, 최적 단면비 ar-opt=0.49이고 이에 대응되는 최대 좌굴하중변수 bmax=1.804이 되며 이 보다 더 큰 좌굴하중변수 b는 존재하지 않는다. 따라서, 이 그림을 통해 최대 좌굴하중을 갖는 말뚝의 설계변수 ar-opt 및 bmax를 결정할 수 있다.
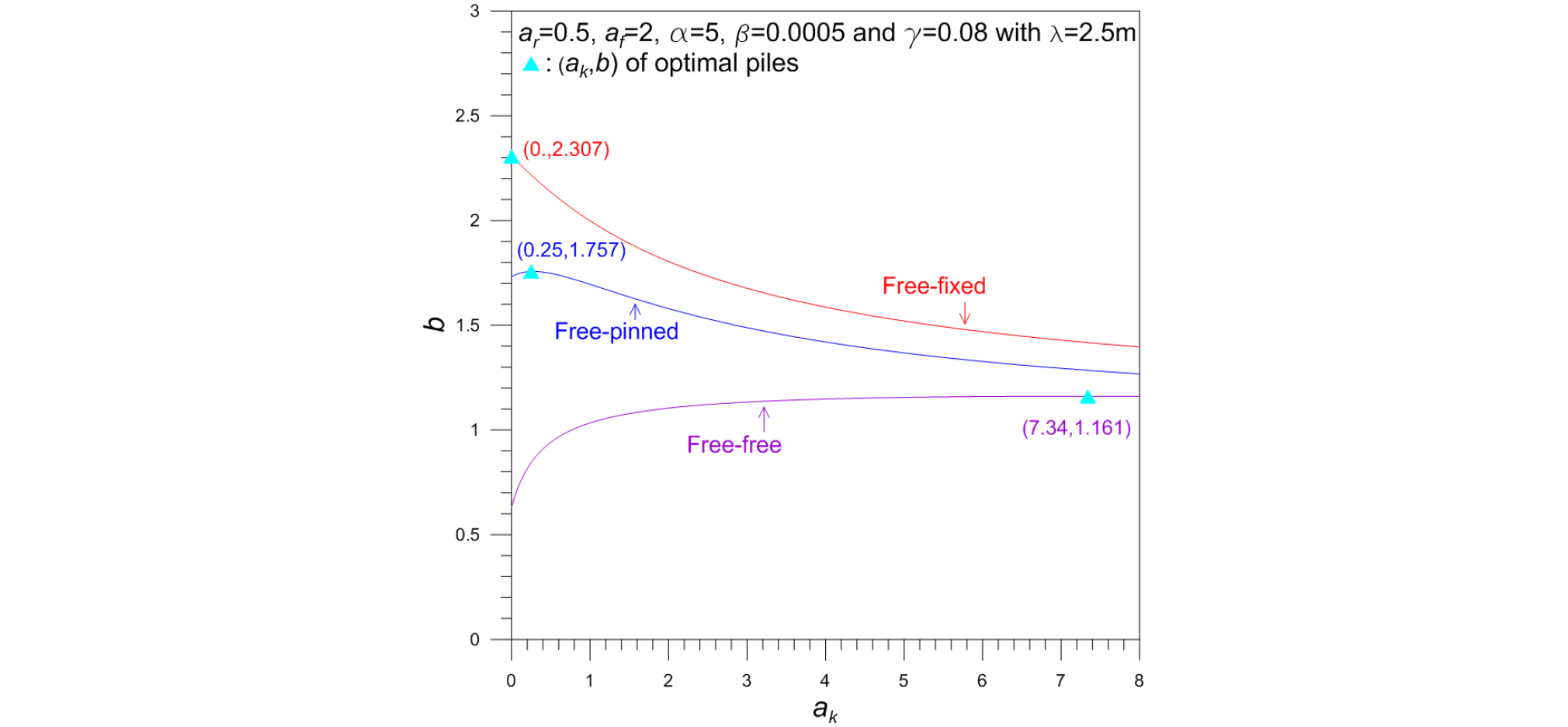
Fig. 5는 테이퍼 말뚝의 좌굴하중변수 b에 대한 지반반력계수비 ak의 영향을 나타낸다. 여기서 ak<1은 지반반력이 깊이에 따라 작아지는 경우이며 ak>1은 그 반대의 경우이다. 이는 점토지반의 경우 과입밀점토와 정규압밀토에 각각 해당한다(Rowe and Booker, 1981; Coduto, 2001). ak=1인 균일지반을 경계로 하여 ak<1에서 지반반력이 좌굴하중변수에 미치는 영향성이 ak>1에 비해 큰 것을 확인할 수 있다. 또한, 지반반력계수비 ak와 말뚝의 단부조건에 따라 좌굴하중변수 b는 증가 또는 감소하는 것을 확인 할 있으며 Fig. 4와 마찬가지로 Fig. 5에서도 최적 말뚝의 (ak-opt, bmax)가 존재(▲로 표시)한다. 예로서 자유-회전 말뚝에서 지반반력계수비 ak-opt=0.25에 대응되는 최적 좌굴하중변수 bmax는 1.757이다.
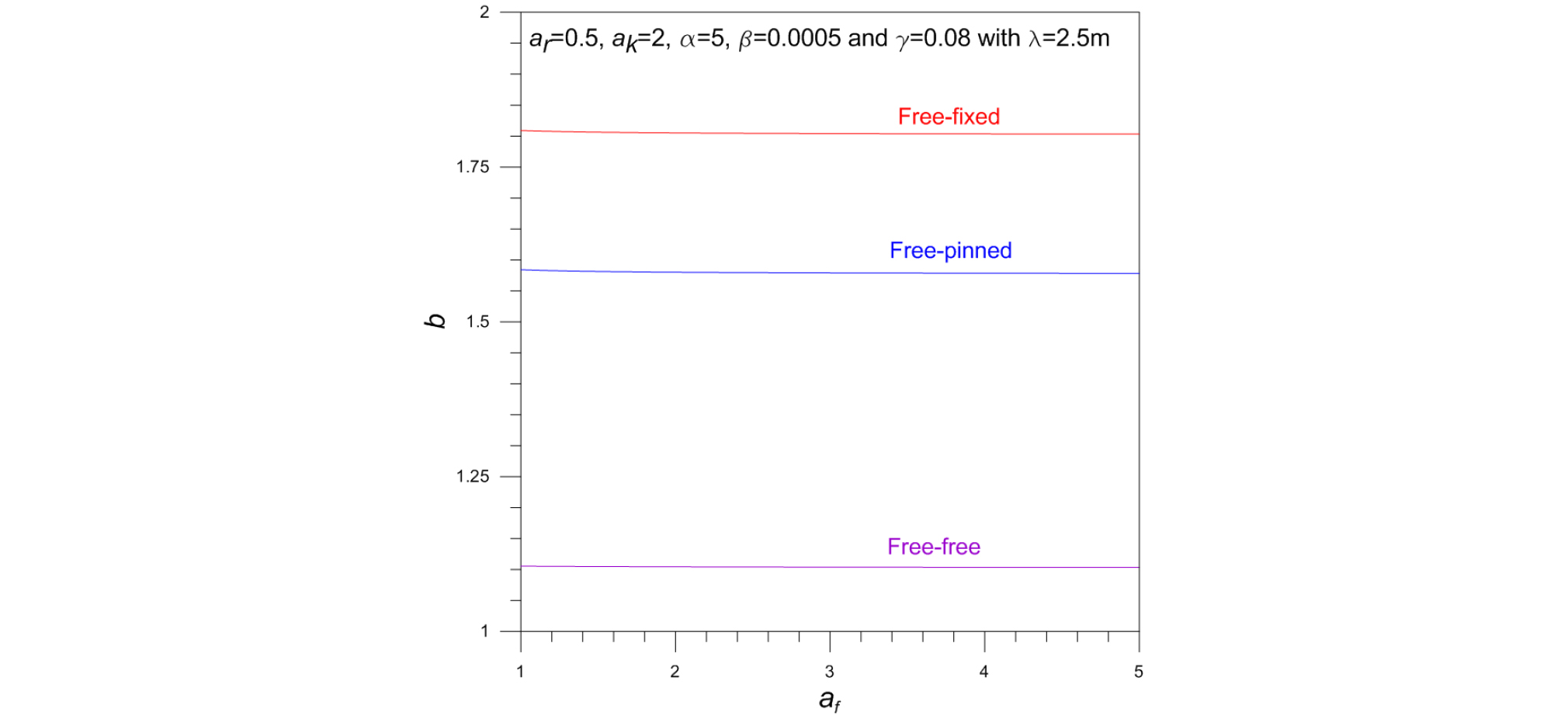
Fig. 6은 테이퍼 말뚝의 좌굴하중변수 b에 대한 주면마찰계수비 af의 영향을 나타내며 예상한 바와 같이 b는 af에 독립적인 것을 확인할 수 있다. 이러한 이유는 이 수치예에서 마찰변수 β는 일정하므로 말뚝 주면에 작용하는 총마찰력()은 af에 상관없이 일정하기 때문이다. 한편, 입력값 β=0.0005는 주면마찰력 fe=31.4kPa(식 (19) 참조)에 대응되는 값으로 이는 연약지반의 주면마찰력을 반영한다.
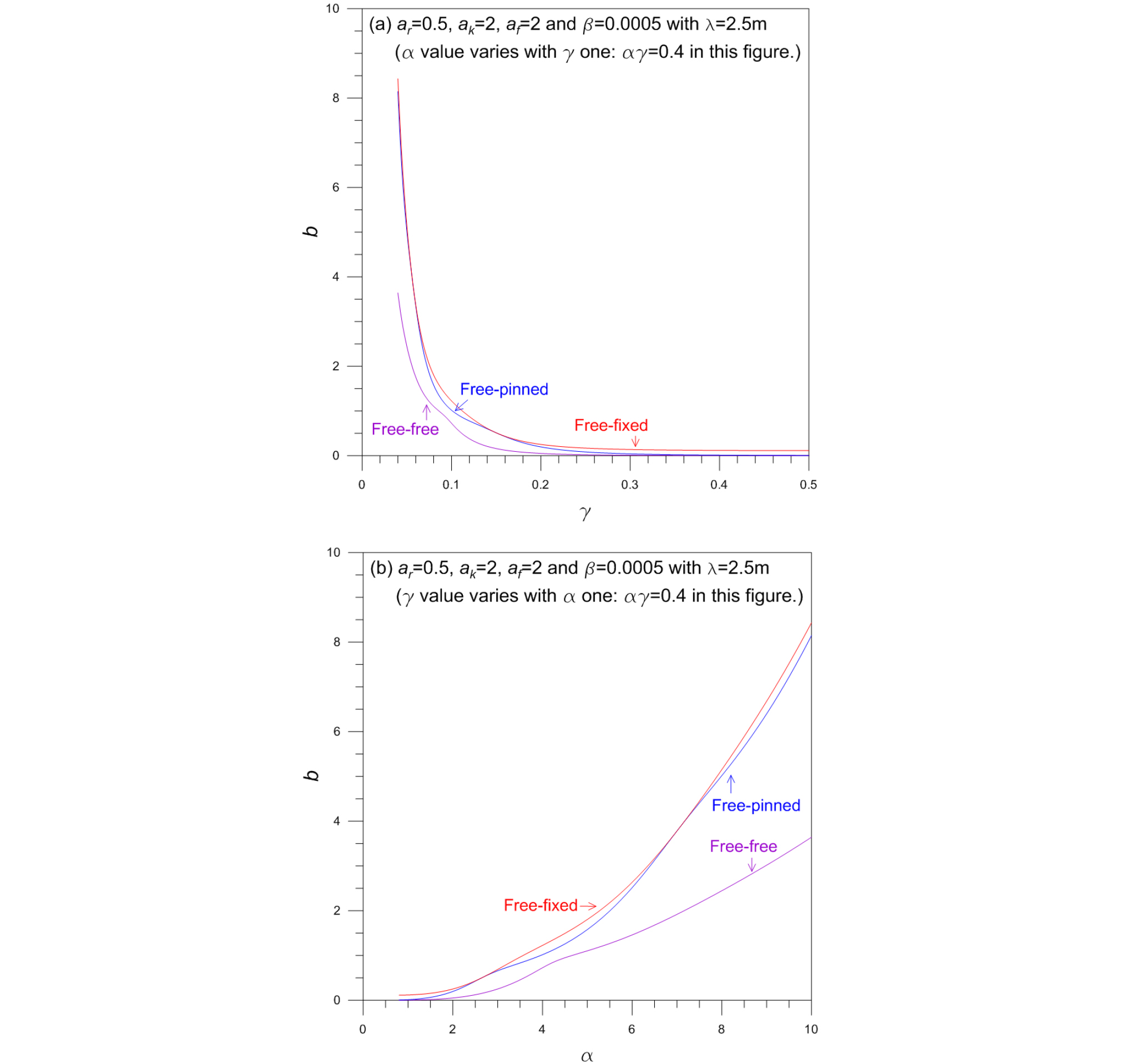
Fig. 7은 테이퍼 말뚝의 좌굴하중변수 b에 대한 장경비 γ 및 특성길이비 α의 영향을 나타낸다. 앞에서 설명한 바와 같이 주어진 수치예에서 γ와 α는 종속적인 관계에 있으므로 Fig. 7에 좌굴하중변수 b에 대한 γ와 α의 관계를 함께 도시하였다. γ의 증가는 α가 감소를 의미하며 이 경우 b는 감소한다. γ > 0.2와 α < 2에서 말뚝은 강성말뚝으로 간주되며 b는 경계조건에 상관없이 서로 근접하고 그 값은 매우 작다. 반면에 γ < 0.1와 α > 4에서 말뚝은 연성말뚝으로 간주되며 이 때 γ의 b에 대한 영향력은 경계조건에 따라 달라지고, γ가 작을수록 크고 α의 경우에는 그 반대이다.
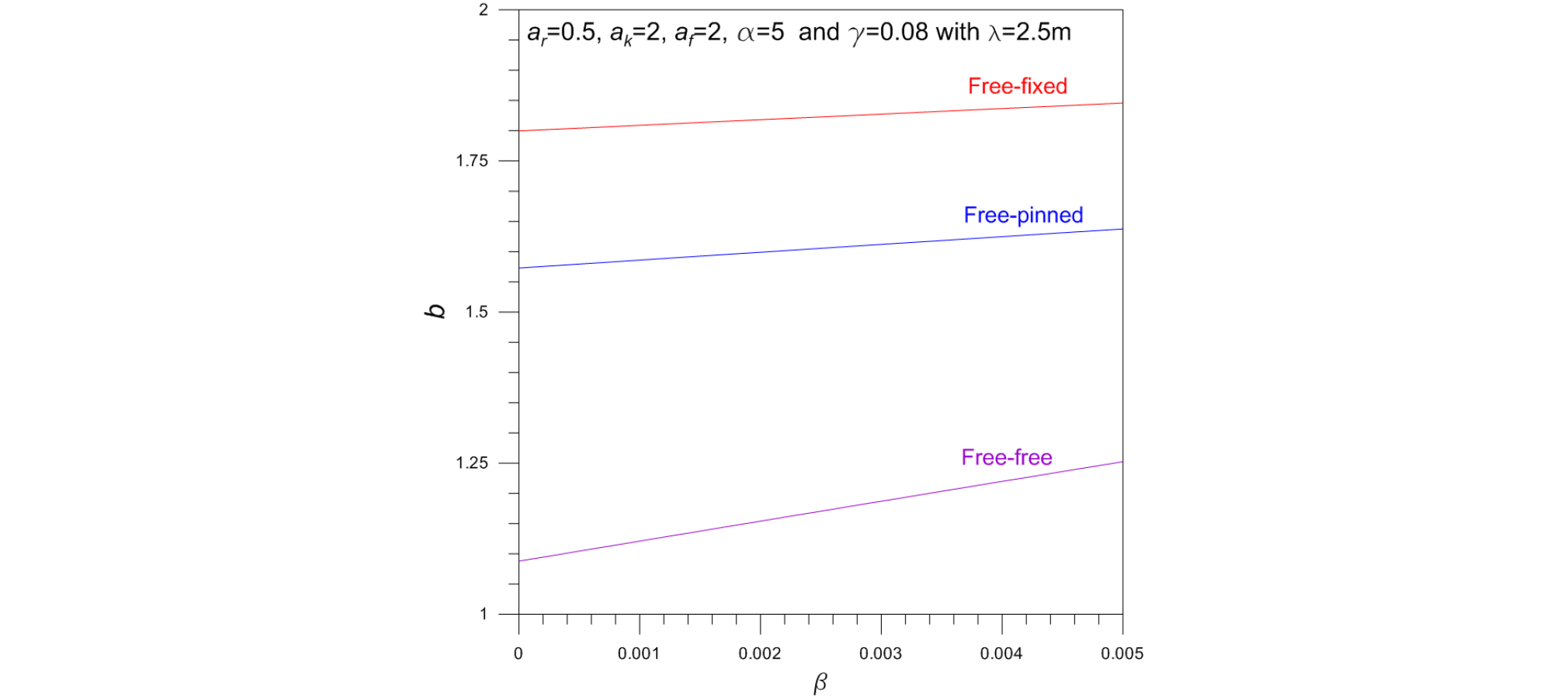
Fig. 8은 테이퍼 말뚝의 좌굴하중변수 b에 대한 마찰변수 β의 영향을 나타낸다. β가 증가하면 b는 거의 선형적으로 증가하며 β에 따른 b의 증가율은 자유-자유 경계조건이 다른 단부조건(자유-회전, 자유-고정)에 비해 크다.
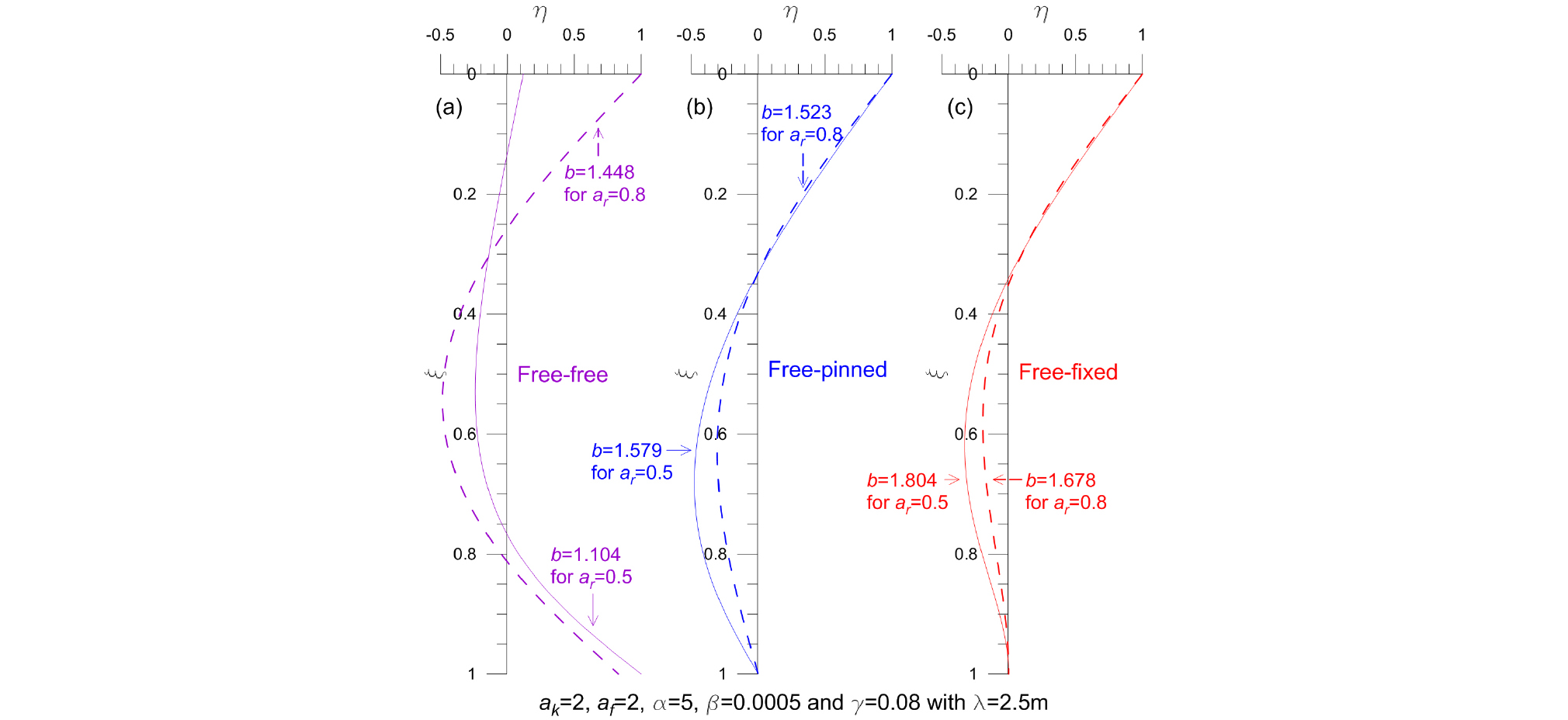
Fig. 9는 테이퍼 말뚝의 좌굴모드 (ξ, η)의 예를 나타낸다. 실선과 점선은 단면비 ar가 각각 0.5와 0.8에 대한 좌굴모드로 말뚝의 테이퍼 각도에 따라 좌굴형상은 변함이 없으나 말뚝 깊이에 따른 횡방향 변위의 크기와 최대 횡방향 발생지점이 크게 차이가 나는 것을 알 수 있다. 또한, 경계조건에 고유의 좌굴형상을 가지며 횡방향 변위에 대한 경계조건의 영향성은 Fig. 9(a)의 자유-자유 경계조건이 다른 단부조건(Fig. 9(b)의 자유-회전, Fig. 9(c)의 자유-고정)에 비해 크다. 특히, 말뚝의 선단부에서 자유인 경우 상대적으로 큰 횡방향 변위가 발생하는 반면 고정은 변위와 처짐각이 0인 것을 확인할 수 있다.
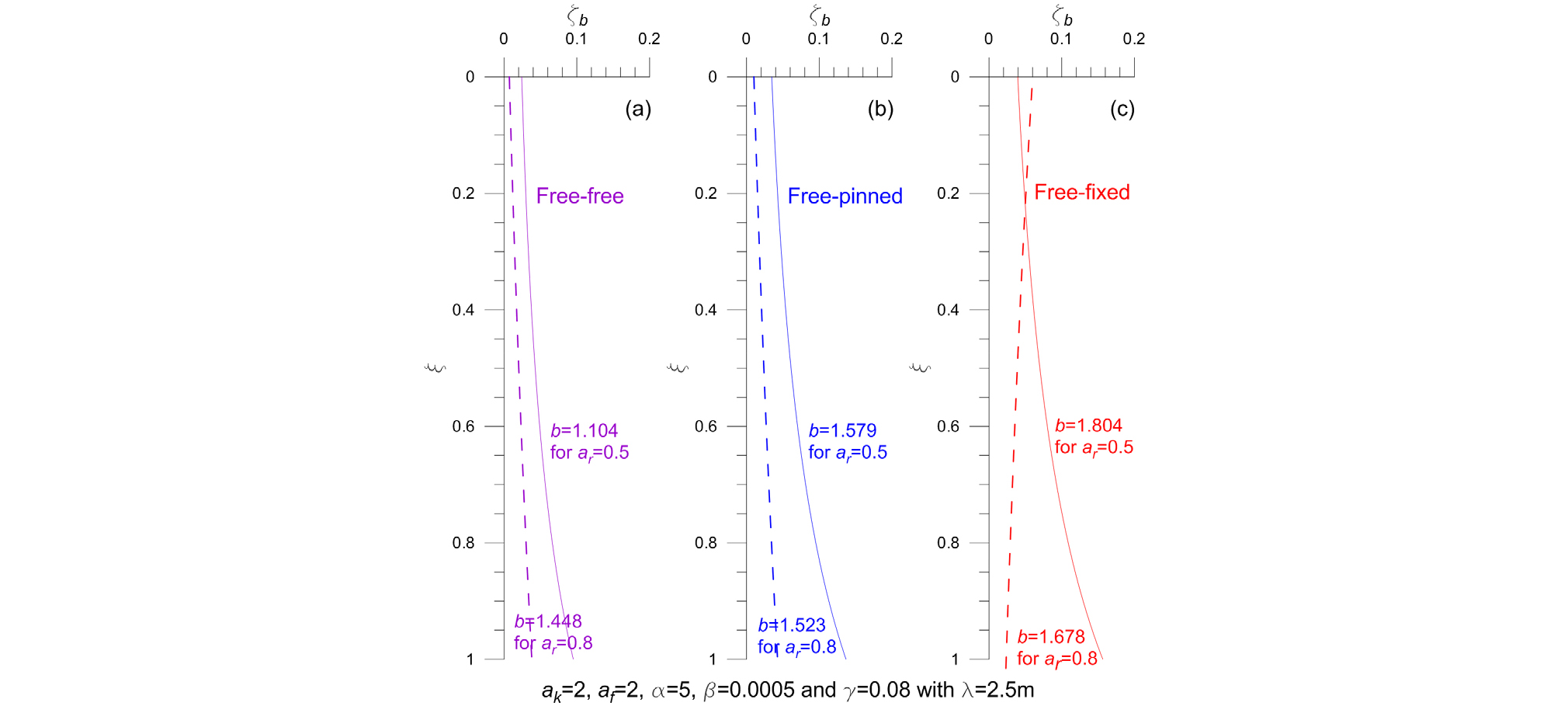
Fig. 10은 좌굴된 테이퍼 말뚝의 깊이 별 좌굴응력변수 ζb의 예로 실선과 점선은 단면비 ar가 각각 0.5와 0.8에 대한 ζb를 나타낸다. 이 수치예의 경우 최대 좌굴응력은 자유-자유, 자유-고정의 경우에 말뚝 하단에서 발생하지만, 자유-고정의 경우에는 말뚝 상단에서 발생한다. 또한, 자유-자유 말뚝의 경우에 ar=0.8의 b가 ar=0.5의 b보다 크지만 ζb는 오히려 더 작다.
6. 결 론
본 연구로부터 얻은 결론은 다음과 같다.
(1) 본 연구의 좌굴하중은 원통형 마찰말뚝에 대한 Gabr et al.(1994)의 값과 잘 일치하였다. 이는 제안된 테이퍼 마찰말뚝의 해석모델과 수치해석방법의 타당성을 보여준다.
(2) 말뚝의 단면비에 따른 좌굴하중변수의 변화를 분석하면 가장 큰 좌굴하중을 갖는 최적말뚝의 단면비를 결정할 수 있다. 지반반력계수비와 좌굴하중변수의 관계에서 최적말뚝의 지반반력계수비가 존재한다.
(3) 말뚝의 좌굴하중변수는 주면마찰계수비에 독립적이나 마찰변수가 증가함에 따라 그 값이 선형적으로 증가한다. 장경비와 특성길이비는 상호 종속적인 관계이며 장경비가 증가하면 좌굴하중변수는 감소하고 특성길이비가 증가하면 좌굴하중변수는 증가한다.
(4) 해석모델은 좌굴하중 뿐만 아니라 좌굴모드와 좌굴응력을 결정할 수 있다. 좌굴모드는 말뚝의 경계조건에 따라 고유의 좌굴형상을 가지며 단면비에 따라 횡방향 변위의 크기와 최대 횡방향 발생지점이 변화한다. 테이퍼 말뚝의 경우 최대좌굴응력 발생지점은 말뚝의 단면비와 두부구속 조건에 따라 말뚝선단이 아닐 수 있다.