1. 서 론
2. 해석 조건
2.1 해석 방법
2.2 지반조건
2.3 지반조건에 따른 해석
3. 해석 결과 및 분석
3.1 지지력 및 침하량 관계
3.2 기존 지지력 이론식과의 비교
3.3 크기효과에 대한 특성
3.4 지반의 전단강도에 따른 특성
3.5 기초형상에 따른 특성
4. 결 론
1. 서 론
구조물을 지지하는 기초는 얕은 기초와 깊은 기초로 분류한다. 얕은 기초는 하중을 지반으로 전달하기 위해 지표부에 직접 놓이는 기초이며 직접기초라고도 한다. 따라서 얕은 기초는 기초 하부지반이 상부하중을 지지할 수 있도록 지지력이 충분히 커야 하며, 지반에 기초로부터 가해지는 압력은 기초지반의 강도정수를 이용하여 계산한 허용치보다 작아야 한다. 얕은 기초는 수많은 건설구조물의 기초로 사용되고 있으며, 지지력을 파악하기 위하여 현재까지 많은 학자들에 의해 이론식이 제안되어 있다. 그러나 이러한 이론식들이 많은 현장에서 현장재하시험 결과와 일치하지 않는 것이 현실이다. 얕은 기초는 기초 깊이(Df)와 기초 폭(B)을 비교하여 그 비가 1 이하이거나(Terzaghi, 1943), 4∼5 이하인 경우(Bowles, 1997) 얕은 기초로 구분할 수 있고, 실제 얕은 기초 지반의 지지력(bearing capacity)과 침하량(settlement)에 기초의 크기효과(scale effect)를 고려해야한다. 이에 대한 연구는 Terzaghi and Peck(1967), De Beer(1965), Das at el.(1996), Zhu at el.(2001) 등의 여러 학자들에 의해 연구가 수행되어졌다. 또한 얕은 기초의 지지력과 침하량 산정방법에는 Terzaghi(1943), Meyerhof(1953), Hansen(1970), Vesic(1973) 등의 정역학적 지지력 공식을 이용한 해석적 방법과 Bond(1961), Meyerhof(1963), D'Appolonia at el.(1968), Peck et al.(1974) 등의 반 경험적 예측방법이 주로 사용되고 있다. 하지만 크기효과를 고려한 지지력 및 침하에 대한 검토는 주로 순수 모래 및 점토를 대상으로 하였으며, 점착력(cohesion)과 내부마찰각(internal friction angle)을 갖는 지반에는 기존의 예측방법으로 크기효과를 고려하는데 한계가 있으며, 실물 크기의 현장시험을 통한 기존 예측방법(Menard, 1965; Baguelin et al., 1978)의 적용성을 검증하는데도 현실적인 어려움이 있다.
이러한 상황에서 크기효과를 고려한 기초의 지지력과 침하특성에 대한 해석적 연구는 주로 2차원적인 평면변형률 조건 상태로 연구되었고(Park et al., 2003; Eun et al., 2006), 실제상황을 잘 모사할 수 있는 3차원 해석에 대한 연구는 부족한 실정이다. 또한 실내시험을 통한 검증에 있어서도 기초 크기의 제한, 지반 상태 등에 대한 실제 조건의 재현에 한계가 있는 상태에서 연구가 이루어졌다(Lee and Kim, 1991; Chung et al., 2003). 따라서 본 연구에서는 수치해석을 이용하여 다양한 조건에 대한 얕은 기초의 지지력 특성을 평가하기 위하여 Kim(2011)의 연구를 기초로 하여 기초크기, 기초형상, 기초지반의 다양한 조건에 대하여 3차원 유한요소해석을 수행하여, 그 해석결과를 토대로 기초 및 지반조건에 따른 얕은 기초의 지지력 특성을 분석하고자 하였다.
2. 해석 조건
2.1 해석 방법
얕은 기초의 지지력 특성을 파악하기 위하여 2차원 및 3차원에 대한 모델링과 해석이 가능한 유한요소해석 프로그램인 MIDAS/GTS를 사용하였다. 기초는 일반적인 콘크리트 물성치를 적용한 탄성 모델을, 지반은 Mohr-Coulomb 모델을 적용하였고, 기초 직경(D) 또는 폭(B)에 대하여 기초두께는 0.4B의 강성체로, 지반은 변위 및 응력의 영향이 미치지 않도록 충분한 영역으로 기초 폭의 10배로 모델링하였다. 유한요소해석은 초기조건 상태를 기초가 지반 상에 놓여있는 상태로 가정하였고, 발생되는 변위에 의한 기초 중앙부분에서의 축 응력을 극한지지력으로 산정하였다(Kim, 2011). 각 경우에 있어 기초의 형상 및 크기가 달라서 하중을 제어하는 대신에 발생되는 침하를 제어하는 방식으로 해석을 수행하였다. 이때 발생된 침하량은 기초 직경 또는 폭의 10%에 해당하는 침하량으로 결정하였으며, 극한지지력도 총 침하량 규준을 적용하여 그 때 발생하는 기초 판의 응력으로 결정하였다. 이는 평판재하시험에서 재하 폭의 약 10% 정도까지 침하가 발생하더라도 관입전단파괴의 파괴양상이 나타난다는 Kim et al.(2012)의 연구를 참고로 하였다.
2.2 지반조건
본 연구의 기초지반은 순수모래, 순수점토, 일반토사로 분류하였다. 순수모래는 점착력이 없는 것으로 가정하였고, 순수점토는 내부마찰각이 없는 것으로 가정하였다(Oh, 1999). 일반토사는 부산・경남 일대의 표토 층의 실내토질시험 결과를 활용하여 지반강도를 산정하였고, 주로 CH, CL, MH, ML, GM, SM으로 분류되었다. 점착력은 분포가 많은 10kN/m2를 기준으로 하여 최대 범위를 30kN/m2으로 설정하였으며, 10kN/m2, 20kN/m2, 30kN/m2로 적용 물성 치를 결정하였다. 또한 내부마찰각은 20°∼30° 범위에 분포하고 있어서 20°, 25°, 30°로 적용 물성 치를 결정하였으며, 탄성계수는 평균치를 적용하였다. 유한요소해석에 적용된 지반정수는 Table 1과 같다.
Table 1. Properties of foundation ground on FEM
2.3 지반조건에 따른 해석
본 연구에서는 기초의 형상을 원형기초, 정사각형기초, 직사각형기초(L=1.5B, L=2.0B, L=3.0B), 연속기초로 변화시켰고, 기초의 크기는 1.0m에서 6.0m까지 1.0m씩 크기를 증가시켰다(Table 2). 기초형상에 따른 각 모델링을 Fig. 1에 나타내었다. 또한 기초 아래의 지반에 대해서 순수점토, 순수모래, 일반토사로 가정하여 지반정수를 적용하였으며, Table 2에는 지반조건에 따른 해석경우를 나타내었다. 유한요소해석은 각 경우에 대하여 기초의 형상 및 크기에 따라 각각 수행하였다.
Table 2. Size of foundations (unit : m)
3. 해석 결과 및 분석
3.1 지지력 및 침하량 관계
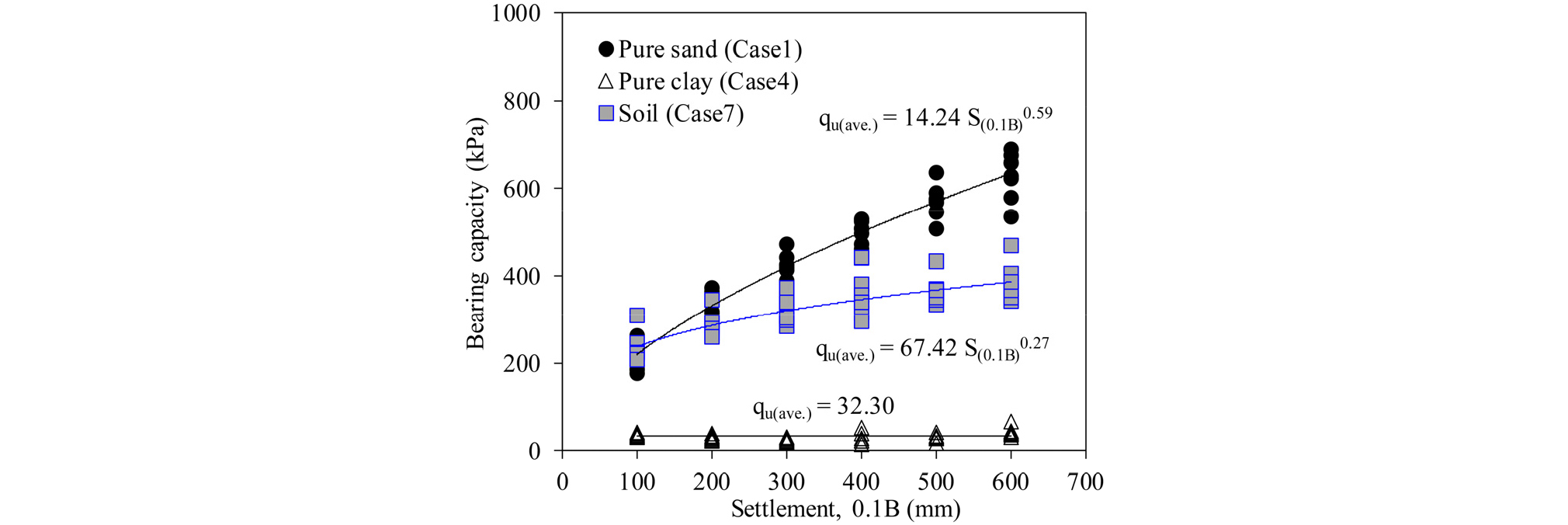
본 연구에서는 극한지지력을 만큼 침하가 발생하였을 때의 지지력으로 검토하였다. 점착력이 없는 순수모래의 경우는 Fig. 2에 보인 바와 같이 주로 기초의 크기에 따라 거듭제곱 및 로그식의 변화양상을 보였고, 내부마찰각이 없는 순수점토의 경우는 기초의 크기에 따라 지지력의 크기 변화가 거의 없는 직선의 변화 형태를 보였으며, 점착력과 내부마찰각이 있는 일반토사의 경우는 거듭제곱의 변화양상을 보였지만 지반강도, 특히 점착력이 커질수록 직선적으로 변화하였다. 순수모래와 일반토사의 경우는 기초가 커질수록 지지력 변화크기가 점차 작아지며, 기초 크기에 따라 지지력이 직선적으로 크게 변화한다는 Terzaghi(1943), Meyerhof(1953), Hansen(1970), Vesic(1973)의 일반적인 이론식에 의한 결과와도 다소 차이가 있는 것을 알 수 있다. Fig. 2에는 대표적으로 순수모래인 Case1, 순수점토인 Case4, 일반토사인 Case7의 침하량 발생에 따른 지지력 결과를 나타내었다(원형기초 D=1∼6m, 정사각형기초 B=L=1∼6m, 직사각형기초 L=1.5B, L=2.0B, L=3.0B 연속기초 B=1∼6m).
3.2 기존 지지력 이론식과의 비교
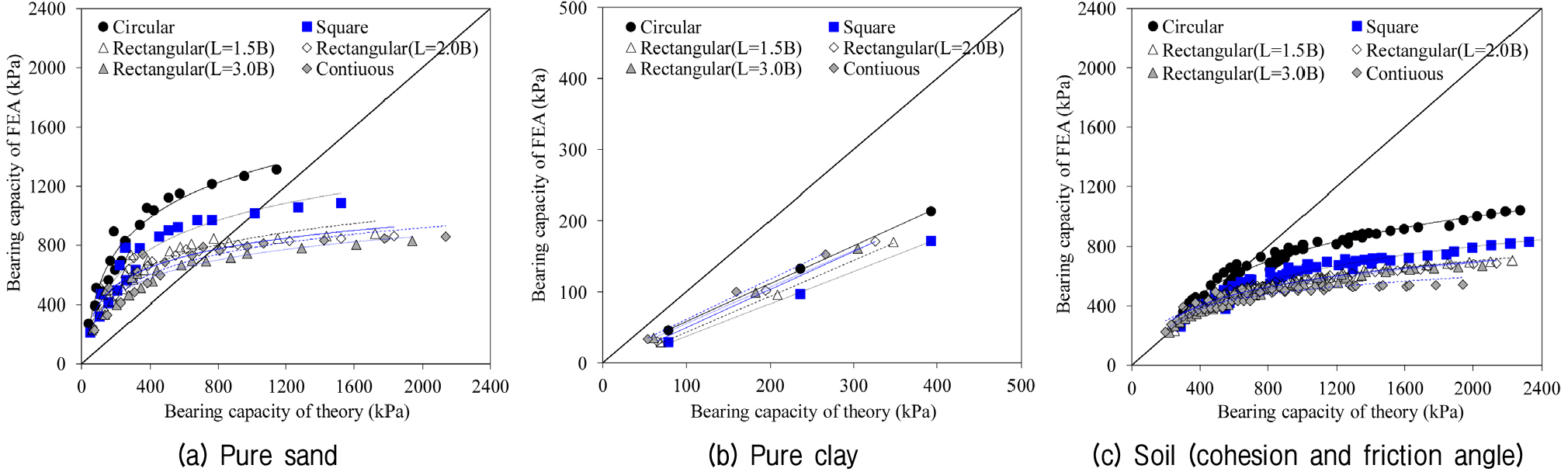
3차원 유한요소해석에 의한 기초의 지지력과 Terzaghi, Meyerhof, Hansen, Vesic의 지지력 이론식에 의한 극한지지력을 비교하였다. 지지력 비(qu(FEA)/qu(theory))는 유한요소해석에서 산정된 지지력과 지지력 이론에 의해 산정된 지지력의 비로 정의하였다. 이론식과 해석에 의한 지지력의 지지력 비에 대한 결과는 Table 3과 Fig. 3에 나타내었다. Table 3의 기초크기는 원형기초, 정사각형기초, 직사각형기초, 연속기초에 대한 각각의 폭이다.
Table 3. Analysis cases by soil types
점착력이 없는 순수모래에서 지지력 비는 기초 크기가 작을수록 크게 산정되었고, 기초의 크기가 커질수록 기초의 형태가 연속기초의 형태일수록 작게 산정되었다. 또한 내부마찰각이 커질수록 지지력비가 작아졌으며, 대체적으로 Terzaghi 식이 해석에 의한 결과에 가장 근접하였고, Meyerhof 식과 Vesic 식은 거의 유사한 지지력비를 나타냈으며, Hansen 식에 의한 결과가 가장 차이가 크게 발생하였다. 이는 이론식에 의한 극한지지력 산정 시 고려되는 지지력계수의 영향으로 판단되었다.
내부마찰각이 없는 순수점토에서는 이론식에 의한 지지력이 크게 산정되었으며, 지지력 이론에 의한 결과와 마찬가지로 유한요소해석에 의한 지지력은 기초 크기에 따라 지지력 변화가 나타나지 않았다. 유한요소해석과 이론식의 결과에 대한 지지력 비는 약 0.4∼0.6 정도로 산정되었다. 이와 같이 이론식에 의한 지지력이 크게 산정된 것은 지지력 계수 Nc가 내부마찰각()의 인자로 극한지지력 계산 시 고려되기 때문인 것으로 판단되었다. 따라서 순수점토에서 해석에 의한 극한지지력 값을 적용할 경우 지지력 비에 대한 충분한 고려가 이루어져야 할 것으로 판단되었다.
점착력과 내부마찰각을 동시에 갖는 일반토사에 대한 유한요소해석과 지지력 이론에 의한 지지력 산정 결과, 지지력 비는 0.3∼1.3 정도로 기초형상과 기초크기에 따라서 비슷하게 나타났고, 지지력 이론식에 따라서도 비슷한 결과를 나타내었다. 지반강도 정수인 점착력과 내부마찰각이 증가할수록 지지력비가 직선적으로 감소하면서 1.0 이하로 나타나는 경향을 보였다.
3.3 크기효과에 대한 특성
기초 크기 변화에 따른 극한지지력의 추정을 위하여 기초 크기와 극한지지력을 기초 크기 1.0m의 해석결과로 정규화한 후 기존의 이론식과 실내 모형실험 결과를 비교・분석하였다. 본 장에서의 지지력 비(qu/qu(1.0))와 기초 폭 비(B/B(1.0))는 기초 크기에 따른 극한지지력과 기초 크기를 1.0m 기초에 대한 결과로 나눈 값으로 정의하였다.
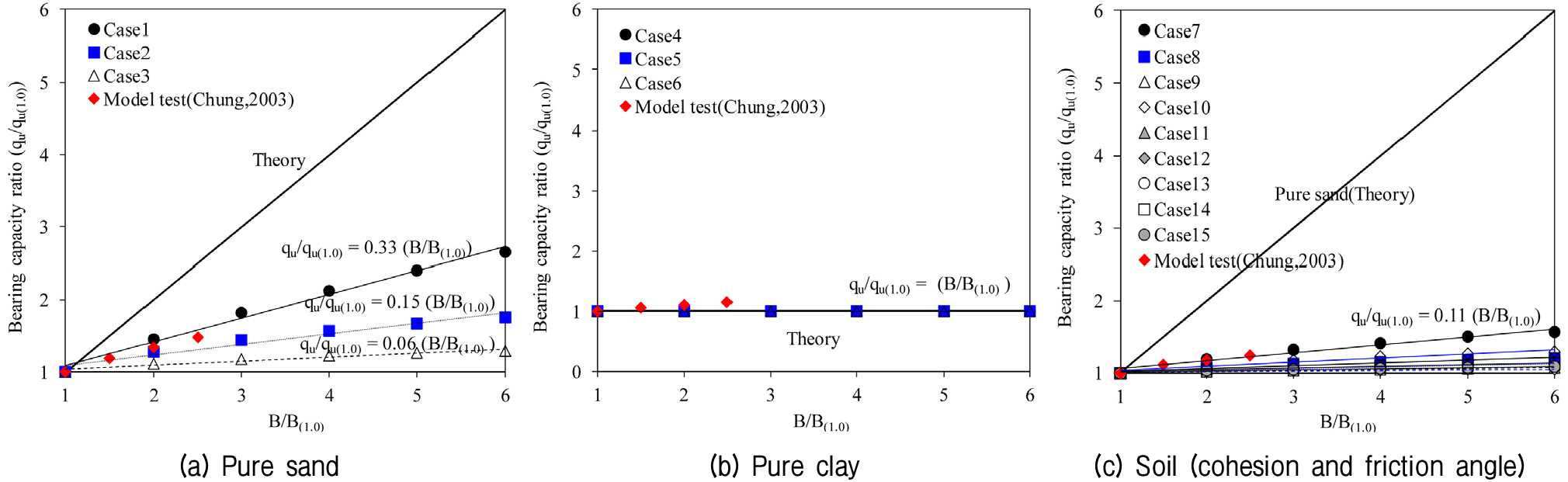
순수모래의 경우 Terzaghi, Meyerhof, Hansen, Vesic의 이론식에 의해 산정된 극한지지력을 1.0m의 기초 크기로 정규화 시키면 지지력비와 기초 폭 비가 기울기 1의 직선적인 관계를 나타냈으며, 내부마찰각이 25°, 30°, 35°로 증가할수록 기초 폭 비에 따른 지지력비의 증가가 작게 산정되어 크기효과(scale effect)의 영향이 적은 것을 알 수 있다. 원형 기초, 정사각형 기초, 직사각형 기초, 연속 기초에서 기초 폭 비가 증가할수록 지지력비가 증가하는 경향을 나타냈지만, 이론식에서와 같이 정비례적으로 증가하지는 않고, 기초 폭 비가 증가할수록 지지력 비는 기초의 형상에 따라 다르게 나타나지만 Fig. 4(a)에서와 같이 이론식에 비하여 평균적으로 내부마찰각이 25°일 경우는 약 30%, 30°일 경우는 약 15%, 35°일 경우는 약 5% 정도로 증가하는 경향이 나타났다. 이와 같은 결과에서 이론식이 과대평가된 것을 알 수 있으며, 실제 기초 적용에 있어 기초크기에 따라 세심한 주의가 필요할 것으로 판단되었다.
Fig. 4(b)와 같이 순수점토는 이론식에 의해 산정된 극한지지력을 1.0m의 기초 크기로 정규화 시키면 지지력 비(qu/qu(1.0))와 기초 폭 비(B/B(1.0))가 기울기 0의 직선적인 관계를 나타냈으며, 점착력 증가에 상관없이 기초 폭 비에 따른 지지력비가 거의 일정하여 기초의 크기효과(scale effect)가 없는 것으로 판단되었다.
점착력과 내부마찰각을 모두 갖는 지반에서는 Fig. 4(c)와 Table 4에서와 같이 내부마찰각이 변하지 않는 동일한 조건에서 점착력을 증가시키면 기초의 크기효과(scale effect)는 점착력이 작은 경우가 더 크게 나타났다. 또한 내부마찰각을 증가시키면 기초의 크기효과(scale effect)는 점착력과 마찬가지로 내부마찰각이 작은 경우가 더 크게 나타났다. 특히, 점착력이 10.0kPa, 내부마찰각이 20°로 지반강도가 작은 경우는 순수모래의 이론식에 비해 지지력비가 약 10%로 산정되었고, 지반 강도가 증가할수록 순수점토와 비슷한 관계를 나타내었다.
Table 4. Bearing capacity ratio (qu(FEA)/qu(theory)) by soil type
기초 크기 효과를 유한요소해석에 의하여 적절성을 검증하기 위하여 Chung et al.(2003)의 실내모형실험 결과와 비교하였다. 모형실험에서는 기초 크기의 제한으로 0.10m, 0.15m, 0.20m, 0.30m 크기에 대한 실험을 수행하였고, 지반종류에 따른 정확한 전단강도에 대한 결과를 판단하기는 곤란하지만 기초 폭 비에 따른 지지력 비는 해석결과와 거의 유사하게 나타나는 것을 확인할 수 있었다(Fig. 4).
3.4 지반의 전단강도에 따른 특성
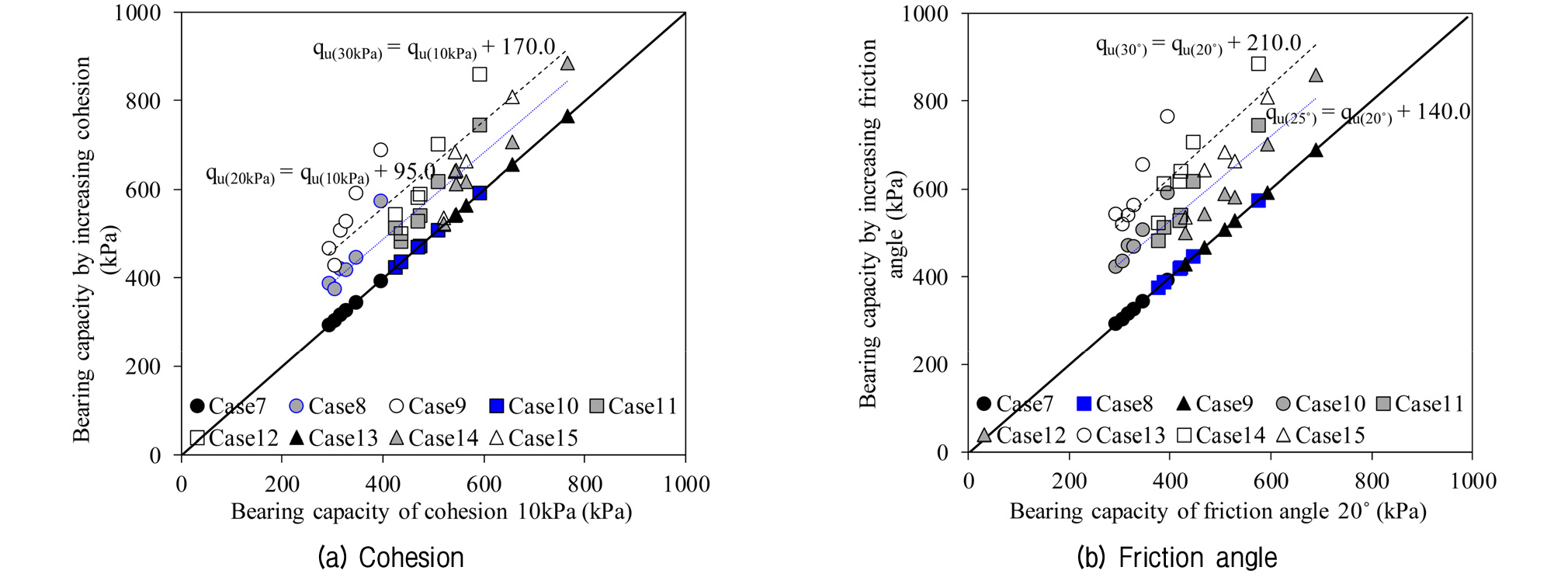
일반토사에 대하여 동일한 지반조건 상태에서 전단강도 정수인 점착력과 내부마찰각을 각각 변화시키면서 유한요소해석을 수행한 결과를 비교하여, 전단강도 증가에 따른 기초의 지지력 특성을 파악하였다. 일반토사에서 지지력을 비교한 결과는 Fig. 5에 나타내었다. 지반의 점착력 및 내부마찰각의 전단강도 증가는 지지력에 영향을 미치는 것으로 나타났다. 하지만 점착력과 내부마찰각은 지지력에 미치는 영향이 다르게 나타나는 것을 확인할 수 있었다. 점착력이 10.0kPa씩 증가할수록 지지력은 약 95.0kPa, 75kPa씩 증가하는 것으로 나타나 점착력이 커질수록 지지력의 증가가 약간씩 감소하는 것으로 나타났다. 또한 내부마찰각의 경우는 5°씩 증가할수록 약 140kPa, 70.0kPa씩 증가하여 내부마찰각이 증가할수록 증가되는 지지력이 1/2배씩 감소하는 것으로 나타났다. 이와 같은 결과에 의해 내부마찰각이 지지력에 미치는 전체적인 영향은 점착력보다는 크지지만 점착력과 내부마찰각의 각각의 증가에 따른 영향성은 점착력이 큰 것으로 나타났다.
3.5 기초형상에 따른 특성
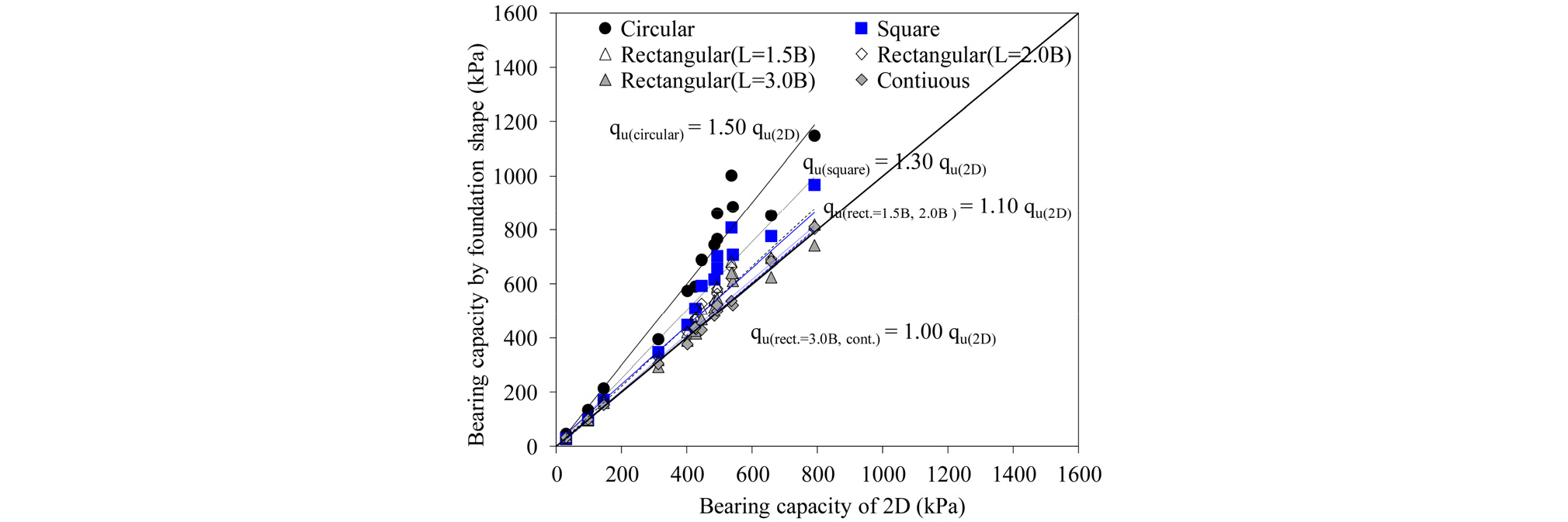
기초형상에 따른 지지력 변화를 알아보기 위해 기초형상을 구현할 수 있는 3차원 해석을 2차원 해석과 비교하여 지지력을 분석하였다. 이때의 지지력 비를 형상계수(shape factor)로 정의하였으며, 기초에 대한 형상계수는 Table 5와 Fig. 6과 같이 나타내었다.
Table 5. Relation of foundation ratio (B/B(1.0)) and bearing capacity ratio (qu/qu(1.0)) for c- soil
|
Friction angle (°) | Cohesion (kPa) | ||
| 10.0 | 20.0 | 30.0 | |
| 20 | 0.11 | 0.04 | 0.01 |
| 25 | 0.05 | 0.02 | 0.01 |
| 30 | 0.04 | 0.03 | 0.02 |
Table 6. Shape factor of foundation by soil types
원형 기초는 50%, 정사각형 기초는 30%, L=1.5B와 L=2.0B의 직사각형 기초는 10%의 지지력 증가를 보였고, L=3.0B의 직사각형 기초와 연속기초는 2차원 해석과 거의 유사한 지지력을 보였다.
4. 결 론
본 연구에서는 얕은 기초의 지지력 특성을 평가하기 위하여 기초크기, 기초형상, 지반 전단강도 등 다양한 조건에 대하여 유한요소해석을 실시하였고, 그 해석결과를 토대로 기초 및 지반조건에 따른 분석을 실시하였다. 그 결과를 요약하면 다음과 같다.
(1) 침하량이 0.1B일 때의 지지력을 극한지지력으로 검토하였을 때 순수모래는 기초의 크기에 따라 거듭제곱 및 로그식의 변화양상을 보였고, 순수 점토는 기초의 크기에 따라 지지력의 변화가 거의 없는 것으로 나타났다. 점착력과 내부마찰각이 있는 일반토사의 경우는 거듭제곱의 변화양상을 보였지만, 점착력이 커질수록 직선적으로 변화하였다.
(2) 유한요소해석결과와 기존 지지력 이론식에 의한 지지력 비(qu(FEA)/qu(theory)) 비교 결과 순수모래는 기초의 크기가 커질수록, 연속기초의 형태일수록 작게 산정되었다. 또한 대체적으로 Terzaghi 식이 해석에 의한 결과에 가장 근접하였다. 순수점토의 지지력 비는 약 0.4∼0.6 정도로 산정되었고, 일반토사는 지지력 비가 0.3∼1.3 정도로 기초형상과 기초크기에 따라서 비슷하게 나타났다.
(3) 기초의 크기에 따른 크기효과(scale effect) 분석 결과 순수모래는 내부마찰각 25°일 경우는 약 30%, 30°일 경우는 약 15%, 35°일 경우는 약 5% 정도로 순수모래는 크기 효과가 없는 것으로 나타났다. 또한 일반토사는 약 10% 이하로 지반 강도가 증가할수록 순수점토와 유사한 경향을 나타내었다.
(4) 내부마찰각이 지지력에 미치는 전체적인 영향은 점착력보다는 컸지만 강도증가와 관련된 영향성은 점착력이 큰 것으로 판단되었다.
(5) 기초형상에 따른 지지력 비에 대한 형상계수는 원형 기초는 1.50, 정사각형 기초는 1.30, L=1.5B와 L=2.0B의 직사각형 기초는 1.10, L=3.0B의 직사각형 기초와 연속기초는 1.0으로 산정되었다.