1. 서 론
2. 취약도 곡선의 작성
2.1 취약도 곡선
2.2 MCS에 의한 확률론적 해석
3. 사면의 확률론적 파괴분포 분석
4. 한계상태함수의 계산
4.1 강우의 침투해석
4.2 사면 안정해석
5. 사면 파괴시간의 확률론적 분석
5.1 지반물성과 해석조건
5.2 결정론적 해석
5.3 확률론적 해석
6. 결 론
1. 서 론
세계적으로 강우로 인한 사면 붕괴가 빈발하고 있으며, 이로 인해 많은 인명 및 재산 피해가 발생하고 있다. 강우의 침투에 의하여 지하수위가 상승하거나 임시 지하수위가 발생하며, 사면표면에 침식이 발생하고 함수비는 증가하여 흙의 단위중량이 증가하게 된다. 함수비 증가로 인한 지반의 전단력 증가와 전단강도의 감소는 강우에 의한 사면파괴를 유발한다(Cho, 2014).
사면 파괴를 일으키는 강우 조건인 사면 파괴 유발 강우기준(rainfall thresholds)은 사면 파괴를 유발한 강우 기록에 기반을 둔 경험적 방법, 또는 물리적 기반의 방법으로 결정된다(Zhang et al., 2016). 다양한 경험적 사면 파괴 유발 강우기준이 강우강도-지속시간의 관계를 나타내는 함수 형태로 제시되었다(Guzzetti et al., 2007). 이들 경험적 강우기준은 장기간에 걸친 기후변동과 사면 파괴의 기록을 반영하지만 지반의 지반공학 및 수리학적 특성을 반영하지 못하며 사면을 통한 강우의 침투과정을 고려하지 못한다(Rahardjo et al., 2007).
물리적 강우기준은 사면파괴를 유발하는 강우강도와 지속시간을 결정하기 위하여 보통 침투해석과 사면 안정해석을 결합한다. 이들 물리적 강우기준(e.g., Pradel and Raad, 1993; Fourie et al., 1999; Cho and Lee, 2002; Cho, 2009)은 경험적 강우기준에 비해, 강우의 침투로 인한 이론적인 사면파괴 과정을 반영하는 장점이 있지만 사면 파괴 발생과 관련한 다양한 불확실성을 고려하지는 못한다.
강우의 침투를 고려한 사면 안정해석은 일반적으로 지반의 특성을 나타내는 변수를 일정한 값으로 취급하는 결정론적 방법을 사용하여 수행된다. 그러나 지반의 거동을 지배하는 지반 변수는 필연적으로 불확실성을 포함하게 되므로 강우의 침투로 인한 사면 파괴 발생 과정 또한 불확실성을 포함하게 된다. 이런 이유로 강우의 침투를 고려한 사면 안정해석을 위해 지반 변수들의 불확실성을 고려한 확률론적 연구가 수행되고 있다(Santoso et al., 2011; Ali et al., 2014; Cho, 2014; Zhang et al., 2014; Dou et al., 2014; Cai et al., 2017). 확률론적 사면 안정해석은 사면파괴와 관련된 불확실성을 합리적으로 고려할 수 있으므로 다양한 강우 조건에서 사면의 성능을 효율적으로 규정할 수 있는 수단을 제공한다.
지반 구조물의 성능은 일정 범위의 하중 조건들에 대한 조건부 확률을 나타내는 취약도 곡선에 의해 특징지어 질 수 있다(Kennedy et al., 1980; Tsompanakis et al., 2010). 취약도 곡선은 전통적으로 지진공학 분야에서 최대지반 가속도의 함수로 구조물의 성능을 평가하기 위해 사용되어져 왔다. 취약도 곡선은 구조물이 노출될 수 있는 하중 범위에 걸쳐 구조물의 신뢰도를 점이 아닌 함수의 형태로 나타내므로, 점으로 표현되는 신뢰도 정보에 비해 구조물에 대한 폭 넓은 신뢰도 정보를 제공할 수 있다. 따라서 최근에는 사면, 댐, 제방 등과 같은 지반구조물의 다양한 손상상태에 대한 위험도 평가 영역에서도 사용이 증가하고 있다(e.g., USACE, 1996; Vorogushyn et al., 2009; Tsompanakis et al., 2010; Wu, 2015; Martinović et al., 2018).
Wu(2015)는 지진과 강우에 대하여 사면의 취약도 곡선을 작성하는 방법론을 제시했다. 사면 안정해석에는 사면파괴가 지반과 불투수성 기반암의 경계면으로부터 상승하는 지하수위로부터 유발된다는 가정으로부터 간단한 무한사면 해석이 적용되었다. Martinović et al.(2018)은 대규모 교통망에 대하여 사면 파괴의 위험도를 정확하게 평가하기 위해서 강우에 의한 얕은 사면 파괴에 대한 취약도 곡선을 작성하는 방법을 제시하였다. 취약도 곡선은 MCS(Monte Carlo Simulation)를 사용하여 강우의 지속에 따른 사면의 신뢰도 변화를 결정함으로써 작성되었다. 사면을 통한 시간에 따른 강우의 침투를 모델링하기 위해 상업용 유한요소 해석 프로그램을 이용하였으며, 침투해석의 결과인 시간에 따른 침윤선의 깊이는 무한사면해석에 의한 사면의 신뢰도 해석에 입력으로 사용되었다.
본 연구에서는 강우의 침투에 따른 토사사면의 파괴에 대한 강우기준을 평가하기 위하여 파괴시간의 확률론적 해석 절차를 제안하였다. 사면 파괴 유발 강우기준은 사면의 취약도 곡선을 기반으로 한 확률론적 사면 파괴분포 분석을 통하여 평가하였다. 취약도 곡선은 시간에 따른 강우의 침투해석 결과를 반영하며 지반의 역학적 특성의 불확실성을 고려한 MCS에 의한 확률론적 사면 안정해석의 결과로부터 강우강도-지속기간의 함수로 생성된다. 확률론적 해석에서 한계상태함수를 계산하기 위하여 강우의 침투해석과 연동된 확률론적 사면 안정해석을 수행하였다. 이를 위해서 유한요소법에 의한 침투해석과 한계평형법을 기반으로 지반의 전단강도 정수의 불확실성을 고려한 확률론적 사면 안정해석이 가능한 상업용 지반해석 프로그램인 Geostudio(2012)를 사용하였다.
제안된 사면의 파괴시간 분석법은 강우의 침투로 인한 사면파괴의 과정을 분석하고 사면 파괴가 발생할 수 있는 시간을 예측하는데 유용하게 사용될 수 있다.
2. 취약도 곡선의 작성
2.1 취약도 곡선
Kennedy et al.(1980)은 지진 공학에서 취약도 곡선을 원자력 발전소 구성 요소의 파괴 빈도와 지진 시 최대 지반 가속도 사이의 확률적 관계로 정의했다. 보다 일반적으로, 취약도 곡선은 시설물 또는 구성 요소가 환경적인 자극을 나타내는 지표의 함수로 정의되는 한계상태에 도달하거나 초과할 확률을 표현하는 관계로 정의될 수 있다(Porter, 2018). 현재 취약도 곡선은 다양한 형태의 기반시설물에 적용되고 있다. 이 곡선은 잠재적 손상에 대한 예측을 제공하며 기반시설물의 총 위험도를 평가하는데 사용된다. 따라서 취약도 곡선은 재해 경감을 위한 비상사태 대비에 필수적인 재난 시 의사 결정 도구로 사용될 수 있다.
취약도 곡선은 발생한 피해의 관찰, 해석 또는 전문가의 판단과 같은 다양한 접근법을 사용하여 도출할 수 있다(Kennedy and Ravindra, 1984). 기후 변화로 인해, 예상되는 극한 강우에 대하여 사면파괴 가능성을 평가하는 일이 점점 중요해지고 있다. 해석적인 방법은 경험적인 방법에 비해, 사면이 실제로 경험하지 못했던 강한 강우조건에 대해서도 취약도를 제공할 수 있으므로 본 연구에서는 해석적 접근법에 의하여 작성한 취약도 곡선을 파괴시간 분석에 활용하였다.
2.2 MCS에 의한 확률론적 해석
취약도 곡선은 지반 구조물이 노출될 수 있는 전체 하중 범위에 걸쳐 지반 구조물의 성능에 대한 정량적 정보를 제공해야 한다. 따라서 주어진 한계상태를 초과할 확률을 계산할 필요가 있다.
확률론적 사면 안정해석의 문제는 흙의 특성을 나타내는 랜덤 변수들의 벡터 X로 정식화되며, 설계변수의 공간에서 안전과 파괴의 경계를 정의하는 한계상태함수 g(X)는 이들 랜덤 변수들에 의해 정의된다(Cho, 2014). 이때 사면의 파괴확률은 파괴영역에 대하여 수행되는 다차원의 적분식으로 표현된다.
| $$P_f=P\left[g(\boldsymbol X)\leq0\right]=\int_{g(\boldsymbol X)\leq0}f_{\boldsymbol X}(\boldsymbol X)d\boldsymbol X$$ | (1) |
여기서, fX는 랜덤벡터 X의 결합확률밀도함수(joint probability density function)이다.
MCS는 확률 분포 및 상관 구조와 일치하는 일련의 랜덤벡터를 생성하고, 생성된 각 표본에 대해 한계상태함수를 계산함으로써 식 (1)의 정확한 해를 구하는 유일한 보편적 방법이다. 파괴확률은 이 과정을 충분한 횟수 반복함으로써 추정된다.
강우의 침투를 고려한 사면 안정은 시간 의존적인 문제이다. 따라서 파괴확률 Pf(t)는 시간 t의 함수로 표현되는 다음과 같은 한계상태함수로부터 계산될 수 있다.
| $$g(\boldsymbol X,t)=F_s(\boldsymbol X,t)-1.0$$ | (2) |
여기서, Fs는 시간에 따른 사면의 안전율이다.
시간에 따른 파괴확률은 각 시간 단계에서 MCS의 실행 횟수에 대한 음의 한계상태함수가 계산되는 횟수의 비율로 정의된다.
| $$P_f(t)\approx N(g(\boldsymbol X,t)\leq0)/N(MC\;runs)$$ | (3) |
MCS의 결과는 주어진 하중강도 LI=p에서 사면파괴에 대한 취약도(fragility) HF이다.
| $$H_F(p,t)=P_f(g(\boldsymbol X,t)\leq0\vert LI=p)$$ | (4) |
식 (4)의 함수는 일정 범위에 걸쳐 주어진 하중 조건에 대한 조건부 누적확률이다. 취약도 곡선은 하중에 따른 구조물의 저항을 나타내지만 특정 하중 발생의 확률이 고려되지는 않는다.
3. 사면의 확률론적 파괴분포 분석
본 연구에서는 취약도 곡선에 기초한 확률론적 사면 파괴시간 분석법을 제안하였다. 이 방법은 산업공학에서 다양한 기계의 유효한 수명을 설명하는데 사용된 기법에서 파생되었다.
취약도 곡선 Pf(t)는 주어진 강우강도에 대하여 시간에 따른 사면의 파괴확률을 제공한다. 사면의 파괴분포 해석에서 시간 t는 강우의 지속 시간을 나타내며, 사면의 전체 수명을 의미하지는 않는다. 그러므로 모델은 강수 침투로 인한 사면의 파괴만을 고려하며 노후화에 따른 사면의 열화는 고려하지 않는다.
만약 흙의 특성 값들이 불확실성을 포함하는 랜덤 변수로 고려된다면, 사면 파괴 발생 시간도 역시 불확실성을 포함하는 랜덤 변수가 된다. 사면파괴까지의 시간을 연속인 랜덤 변수 T(T ≥ 0)라 하면, 사면파괴의 누적확률분포(cumulative distribution function, CDF) Pf(t)는 다음과 같이 정의될 수 있다.
| $$P_f(t)=\Pr\{T<t\}$$ | (5) |
여기서, 이다.
주어진 시간 t에 대하여, Pf(t)는 시간 t 이전에 사면의 파괴가 발생할 확률을 의미한다. t가 정상상태의 흐름이 발생하는 시간 tst에 접근함에 따라 Pf(t)는 최대값인 Pfmax에 도달한다. MCS를 수행할 때 샘플링된 모든 램덤 변수들의 표본에 대하여 사면의 파괴가 예측된다면 Pfmax는 1이 된다.
파괴분포의 모양을 나타내는 확률밀도함수(probability density function, PDF)는 식 (6)과 같이 정의된다(Zhang et al., 2014; Dou et al., 2014):
| $$f(t)=\frac{dP_f(t)}{dt}$$ | (6) |
여기서, f(t) ≥ 0이고 이다.
확률밀도함수 f(t)가 주어지면, 파괴확률은 곡선 하부의 면적으로 계산된다.
| $$P_f(t)=\int_0^tf(t)dt$$ | (7) |
사면 파괴분포의 해석을 위해서, 곡선 하부의 전체 면적이 1이 되도록 f(t)를 Pfmax로 정규화하여 확률밀도함수 f'(t)를 도입하였다. 이때 f(t)는 MCS를 수행한 모든 표본에 대한 사면파괴의 확률밀도를 나타내나 f'(t)는 파괴가 발생한 표본만을 대상으로 한 사면파괴의 확률밀도를 나타낸다. 사면파괴 발생 시간의 분포는 실제로 파괴가 발생한 표본만을 대상으로 분석하여야 하므로 확률밀도함수 f'(t)를 사용하였다. 따라서, 이고 이다.
평균(mean), 중앙값(median) 및 최빈값(mode)은 신뢰성에 대한 가장 일반적인 세 가지 측정 척도이다. 평균은 전체 모집단을 대표하는 중심 경향(central tendency) 척도로 가장 널리 사용되며, 강우에 의한 사면 파괴가 발생하기까지의 평균 시간은 다음과 같이 확률밀도함수 f'(t)에 의해 정의되는 확률분포의 기댓값으로 정의된다.
| $$t_{mean}=E(T)=\int_0^\infty tf'(t)dt$$ | (8) |
사면 파괴분포의 또 다른 중심 경향 척도인 사면파괴 발생 시간의 중앙값은 다음과 같이 정의된다.
| $$P_f'(t_{med})=\int_0^\infty f'(t)dt=0.5$$ | (9) |
중앙값은 확률분포를 동등한 두 부분으로 나누므로 파괴의 50%는 중앙값 시간 이전에 발생하고 50%는 중앙값 시간 이후에 발생한다.
가장 빈번하게 관찰되는 파괴발생 시간인 최빈값은 다음과 같이 정의된다.
| $$f'(t_{\mathrm{mode}})=\max_{0\leq t<\infty}f'(t)$$ | (10) |
시간 의존적인 사면의 파괴 과정을 분석하기 위해서는 식 (5)와 같이 사면의 파괴확률이 시간에 대하여 연속적인 형태로 표현되어야 한다. MCS에 의한 사면의 파괴확률은 임의의 시간 단계에 대해서만 구해지므로 시간에 대하여 연속적인 형태로 표현하기 위하여 와이블분포(Weibull distribution), 정규분포(normal distribution) 및 대수정규분포(lognormal distribution) 등의 확률분포 함수가 유용하게 사용될 수 있다.
Cho(2019)는 대수정규분포를 사용하여 사면의 얕은 파괴에 대한 파괴분포 해석을 수행하였다. 랜덤 변수인 T(사면파괴 발생까지의 시간)가 대수정규분포를 따른다면, T의 대수값은 정규분포를 따를 것이다. 대수정규분포의 확률밀도함수는 다음과 같다.
| $$f'(t)=\frac1{\sqrt{2\pi}st}\exp\left[-\frac1{2s^2}\left(\ln\frac t{t_{med}}\right)^2\right]\;\;\;\;\;\;\;\;\;\;t\geq0$$ | (11) |
여기서, s는 형상변수(shape parameter)이며 tmed는 사면파괴 발생까지의 중앙값에 해당하는 시간이다.
대수정규분포는 t의 양의 값에 대해서만 정의되므로 정규분포에 비해 파괴분포로 더 적합하다(Ebeling, 1997).
대응하는 누적확률분포 Pf(t)는 다음과 같다.
| $$P_f(t)=P_f'P_{fmax}=\Phi\left\{\frac1s\ln\frac t{t_{med}}\right\}P_{fmax}$$ | (12) |
여기서, Φ는 표준정규분포의 CDF이다.
본 연구에서는 강우의 침투로 인한 사면의 시간 의존적 파괴확률을 나타내기 위하여 대수정규분포를 사용하여 사면의 파괴시간을 확률적으로 해석하였다. 더불어 시간 의존적인 사면의 파괴확률이 특정 확률분포를 따르지 않는 경우에도 적용할 수 있도록 smoothing spline 모델을 사용하여 연속적인 함수 형태로 표현하는 기법을 제안하였다.
4. 한계상태함수의 계산
한계상태함수를 계산하기 위하여 강우의 침투로 인한 불포화 토사 사면의 안정성을 평가하였다. 강우의 침투를 고려하기 위하여 포화-불포화 침투해석을 수행하였고 침투해석의 결과를 불포화 전단강도를 고려하는 한계평형법에 의한 사면 안정해석에 적용하여 시간에 따른 안전율의 변화를 계산하였다.
4.1 강우의 침투해석
강우의 침투로 인한 사면의 안정을 해석하기 위해서는 침투로 인한 지반에서의 간극수압의 변화를 파악해야 한다. 토사사면의 경우 포화 및 불포화된 지반 구조체를 이루고 있으므로 강우의 침투거동을 해석하기 위해서는 포화 및 불포화 영역에서의 흐름을 고려하여야 한다. 불포화토에서의 물의 흐름도 연속된 물의 흐름 통로를 통해 이루어지므로 Darcy의 법칙을 적용할 수 있다. 이 경우 불포화토에서의 흐름 문제를 해석하기 위해서는 불포화 상태에 따른 투수계수를 사용해야 한다. 본 연구에서는 2차원 유한요소 해석을 통하여 강우의 침투거동을 해석하여 그 결과를 사면 안정해석에 적용하였다.
4.2 사면 안정해석
강우의 침투에 의한 간극수압 분포를 반영하여 한계평형법(Spencer 방법)으로 사면의 안정해석을 수행하였으며 최소안전율을 주는 비원호 임계 파괴면(critical failure surface)을 탐색하였다. 이때 강우의 침투에 따른 불포화 전단강도의 변화를 고려하였다.
흙에서 양의 간극수압은 유효응력을 감소시켜 전단강도의 감소를 유발하지만 흙의 모관흡수력 혹은 음의 간극수압은 흙의 유효응력을 증가시켜 지반의 전단강도를 증가시키는 효과가 있다. 사면의 파괴면의 바닥에서 모관흡수력에 의한 전단강도의 증가를 계산하기 위해 를 사용하며 의 상한값은 내부마찰각 이다. 는 지반의 포화도에 따라 달라지는 값이므로 흙의 함수특성곡선으로부터 모관흡수력에 의한 강도증가 효과를 정량화하기 위한 많은 연구가 수행되었다. Vanapalli et al.(1996)은 식 (13)과 같이 불포화 전단강도 τf를 계산하기 위한 식을 제안하였으며 본 연구에서는 이 식을 적용하여 불포화 전단강도를 고려하였다.
| $$\tau_f=c'+(\sigma_n-u_a)\tan\phi'+(u_a-u_w)\left[\left(\frac{\theta_w-\theta_r}{\theta_s-\theta_r}\right)\tan\phi'\right]$$ | (13) |
여기서, θw는 지반의 체적함수비, θs는 포화체적함수비, θr은 잔류체적함수비, σn은 총 수직응력, ua는 공기압, uw는 간극수압, c'은 점착력이다.
5. 사면 파괴시간의 확률론적 분석
본 연구에서는 실용적으로 널리 사용되고 있는 상업용 지반해석 프로그램인 Geostudio(2012)를 사용하여 강우에 의한 사면의 안정해석을 수행하였다. 불포화 상태에서 지반의 수리학적 특성을 나타내는 변수의 불확실성은 사면의 거동과 연관되는 간극수압과 유효응력에 직접적인 영향을 미치므로 그 영향을 고려하기 위한 연구가 수행되어 왔다(e.g., Santoso et al., 2011; Ali et al., 2014; Cho, 2014). 그러나 실무에서 사용되고 있는 상업용 지반해석 프로그램들 중에는 지반의 수리학적 특성을 나타내는 변수들의 불확실성을 고려하여 확률론적 사면 안정해석을 수행할 수 있는 해석 프로그램이 없으므로 본 연구에서는 지반의 역학적 거동특성을 나타내는 강도정수들의 불확실성만을 고려하여 확률론적 사면 안정해석을 수행하였다. 물론, 본 연구에서 제안된 파괴분포 해석법은 확률론적 해석법의 종류와 난이도와는 상관없이 적용할 수 있는 보편적 방법이다.
5.1 지반물성과 해석조건
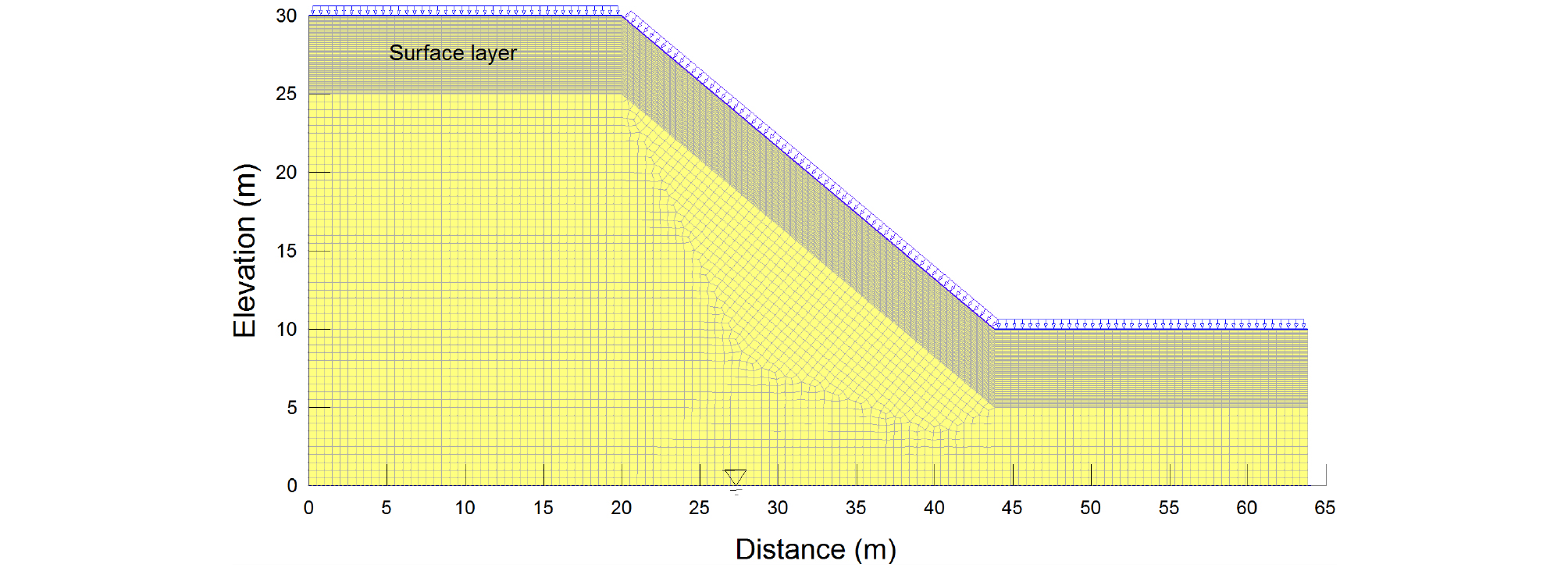
Fig. 1과 같이 기울기가 40°인 높이 20m의 균일한 토사사면에 대하여 해석을 수행하였다. 강우의 침투에 의하여 지표면 부근의 간극수압은 짧은 시간에 급격하게 변하므로 이를 정확하게 계산하기 위해 지표면으로부터 5m 깊이는 surface layer로 모델링하여 매우 작은 요소로 이산화 하였다.
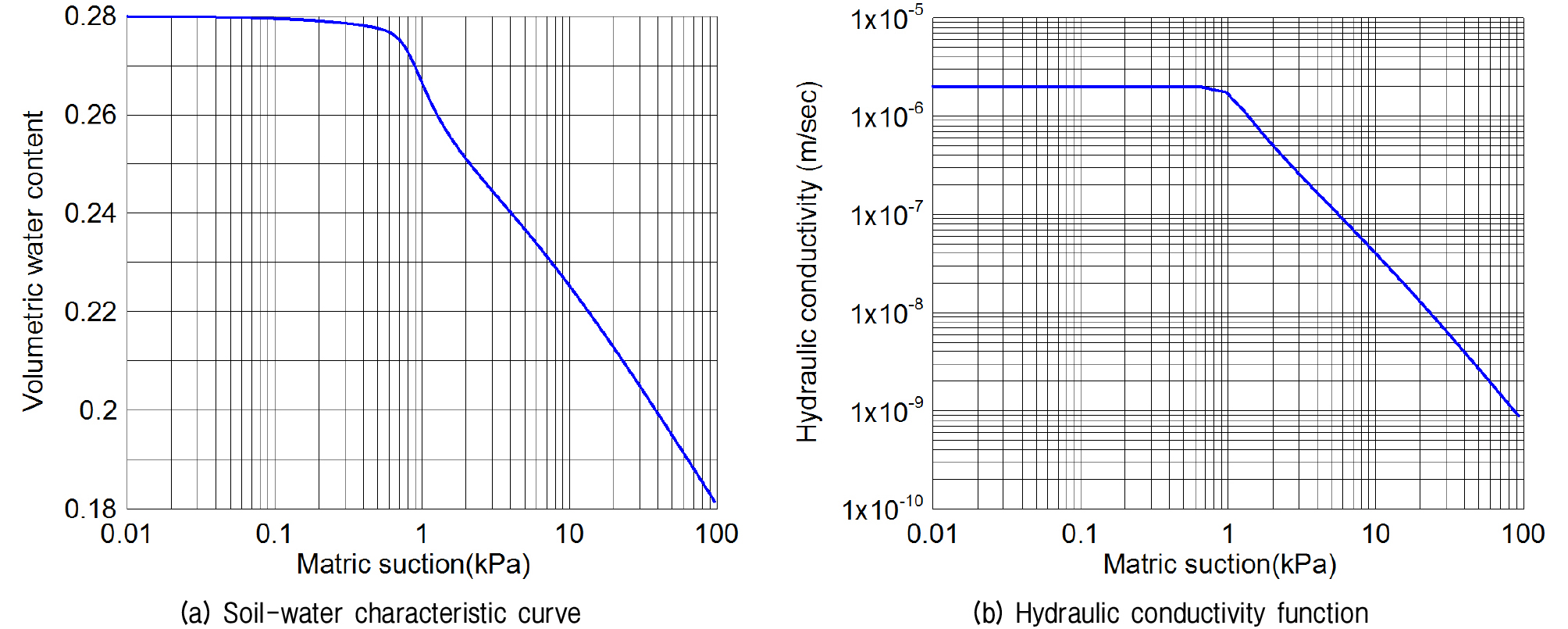
Fig. 2의 수리학적 물성은 기존의 문헌에서 모래질 흙으로 분류되는 전형적인 화강풍화토의 값을 선정하여 사용하였다(Kim, 2003). Fig. 2(a)는 압력판추출시험(pressure plate test)에 의해 구한 함수특성곡선을 나타내며 Fig. 2(b)의 투수계수함수는 Fredlund et al.(1994)의 방법으로 예측하였다. 지하수위는 Fig. 1과 같이 해석영역의 바닥에 존재하는 것으로 가정하였다. 시간 의존적인 강우의 침투를 모델링하기 위해서는 수리학적 초기조건이 지정되어야 한다. 침투해석 시 초기 모관흡수력을 정의하기 위하여 지하수위를 입력하거나, 지반의 모관흡수력을 측정한 값을 사용할 수 있다. 본 연구에서는 초기 모관흡수력이 지하수위로부터 거리에 따라 직선적으로 증가하되 기존의 현장계측 연구를 근거로 지반의 특성과 우기 중임을 고려하여 최대 20kPa의 값을 갖도록 적용하였다(Kim et al., 2013).
강우를 모사하기 위하여 시간에 따라 일정한 강우강도를 사면표면에 작용시켰다. p의 일정한 강우강도가 연직방향으로 작용하면 기울기 β인 사면 표면에 수직하게 작용하는 강우강도는 pcosβ이다. 사면의 표면에서 강우강도가 흙의 침투능을 넘어서는 폰딩이 발생하면 여분의 강우는 경사진 사면의 표면을 따라 유출된다는 가정에 따라 표면에서의 간극수압이 0보다 크지 않도록 경계조건을 적용하였다.
Table 1은 사면 안정해석에 사용된 지반의 역학적 물성치를 나타낸다. 본 연구에서는 Phoon and Kulhawy(1999)가 제시한 지반정수의 변동 범위를 고려하여 변동계수를 결정하였다. 단위중량, 점착력 및 내부마찰각의 변동계수에 따른 파괴확률의 민감도 분석이 이루어진 기존 연구(Kim and Cho, 2006)에 의하면 확률론적 해석에 있어서 흙의 단위중량의 변동성은 다른 변수들에 비해 작아 해석결과에 큰 영향을 미치지 않으므로 해석의 효율성을 고려하여 결정론적으로 고려하였다. 점착력과 내부마찰각은 확률적으로 대수정규분포를 따른다고 가정하였다. 랜덤 변수들의 샘플링을 위해서는 변수들 간의 상관성을 고려해야 한다. 전단강도 정수들 사이의 상관성을 고려하기 위해서는 교차상관계수(cross correlation coefficient) r(c,)가 필요하다. Wolf(1985)는 점착력 c와 내부마찰각 의 상관계수에 대하여 압밀-비배수 시험으로부터 r=0.25, 압밀-배수 시험으로부터 r=-0.47을 제시하였다. Yucemen et al.(1973)은 -0.49≤r≤-0.24의 값을 보고하였고 Lumb(1970)은 -0.7≤r≤-0.37을 제시하였다. 음의 상관관계는 낮은 점착력 값이 높은 내부마찰각과 연관됨을 의미한다. 다시 말해, 점착력과 내부마찰각 사이의 음의 상관관계는 계산된 전단강도의 불확실성이 전단강도를 모델링하는데 사용된 두 가지 매개 변수 값의 결합된 불확실성(비상관의 경우)보다 더 작음을 의미한다. 본 연구에서는 r=-0.5를 기본값으로 사용하였으며 상관계수의 영향을 고려하기 위하여 -0.7≤r≤0.5의 범위를 고려하였다.
5.2 결정론적 해석
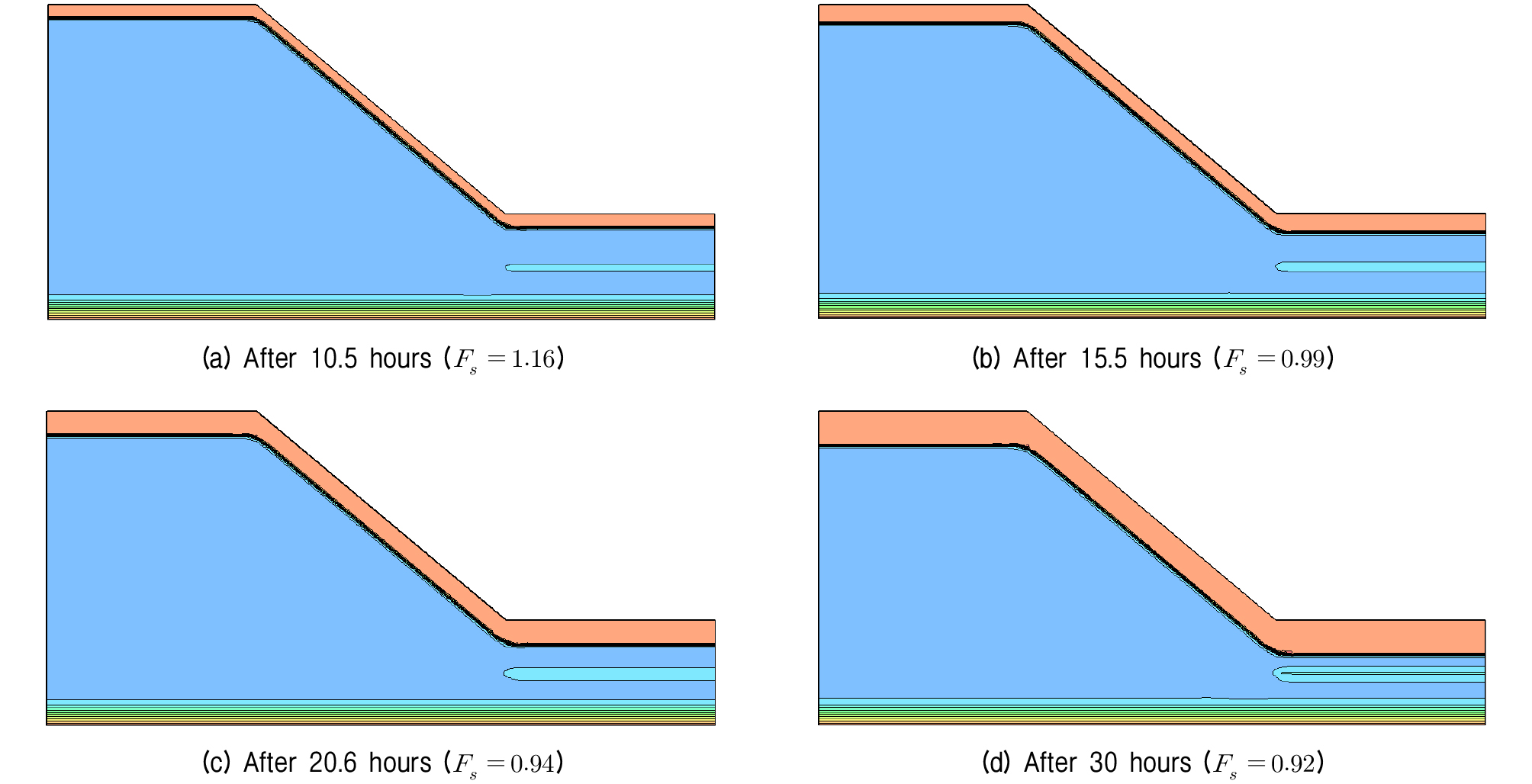
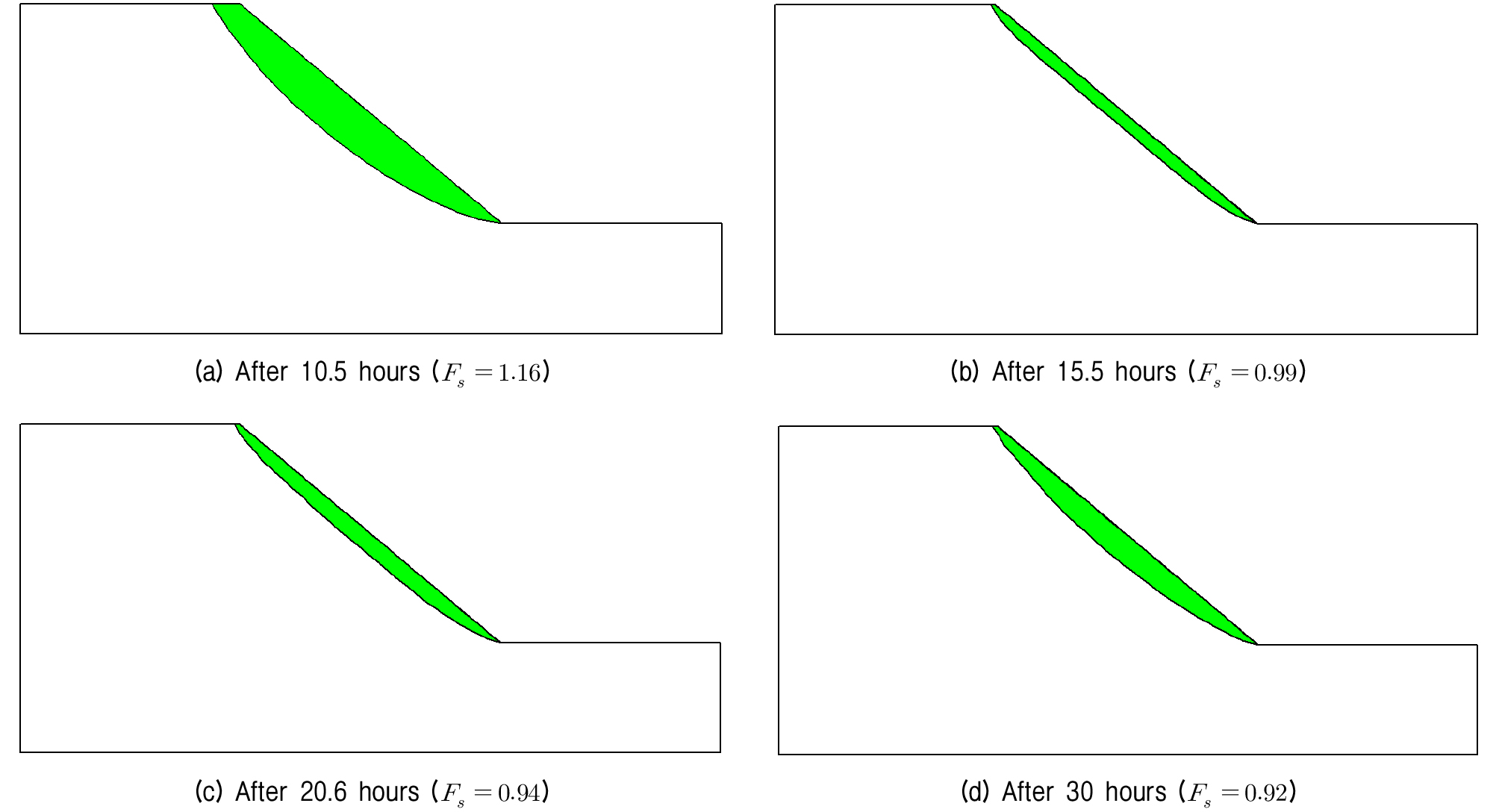
확률론적 해석을 수행하기 전에 강우의 침투에 의한 사면의 거동을 살펴보기 위해 결정론적 해석을 수행하였다. 해석은 Table 1에 제시된 변수들의 평균값을 이용하였다. 해석은 사면의 표면에 작용하는 강우강도 p를 변화시키며 지속시간 30시간에 대하여 수행하였다. Fig. 3은 여러 해석결과 중 p=0.8ks(ks는 지반의 포화투수계수)일 때 시간에 따른 침윤선의 변화를 나타낸 것이며 Fig. 4는 대응하는 사면 안정해석의 결과인 임계 파괴면과 안전율을 나타낸다.
Table 1. Input parameters used for slope stability analysis
| γd (kN/m3) | c (kPa) | (°) | Correlation coefficient | |
| Mean | 20 | 2 | 32 | -0.7≤r≤0.5 |
| COV (%) | - | 20 | 10 | |
| Distribution | - | Lognormal | Lognormal | - |
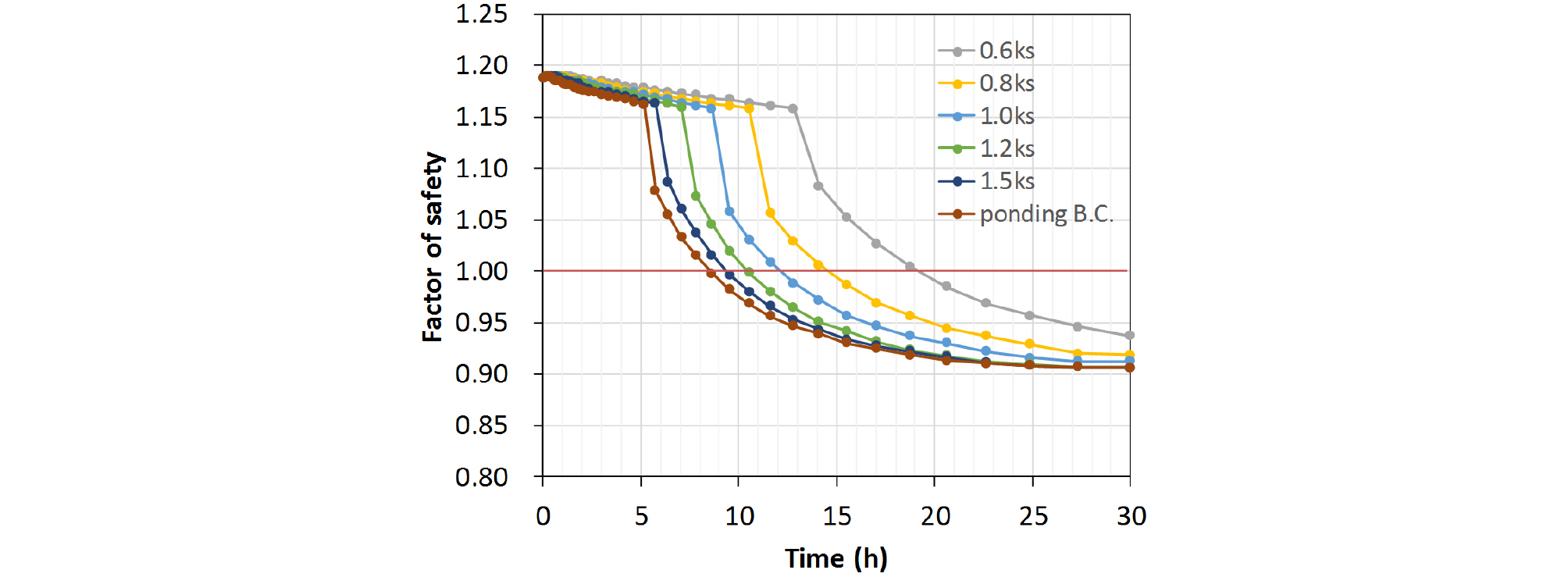
Fig. 5는 30시간 동안에 안전율의 변화가 크게 발생한 강우강도에 대하여 시간에 따른 안전율의 변화를 나타낸 것이다. 이때 강우강도 p가 증가할수록 안전율이 빨리 감소하고 있음을 알 수 있다. 강우의 초기에는 시간에 따른 안전율의 감소율이 작지만 어느 시점을 넘어서면 안전율의 감소율이 커져 안전율이 크게 감소하고 파괴상태에 도달하며 점차 일정한 값으로 수렴하는 결과를 나타내고 있다. 안전율 곡선의 감소율이 강우 초기에는 작다가 일정 시간 경과 후 커지는 이유는 시간에 따라 임계 파괴면이 변하기 때문이다. 즉, 강우의 초기에는 사면의 깊은 위치에 임계 파괴면이 형성되어 강우에 의한 영향이 작게 반영되다가 침투로 인하여 사면표면부에 임계 파괴면이 형성된 이후에는 강우의 영향이 크게 반영되어 안전율이 크게 감소한다.
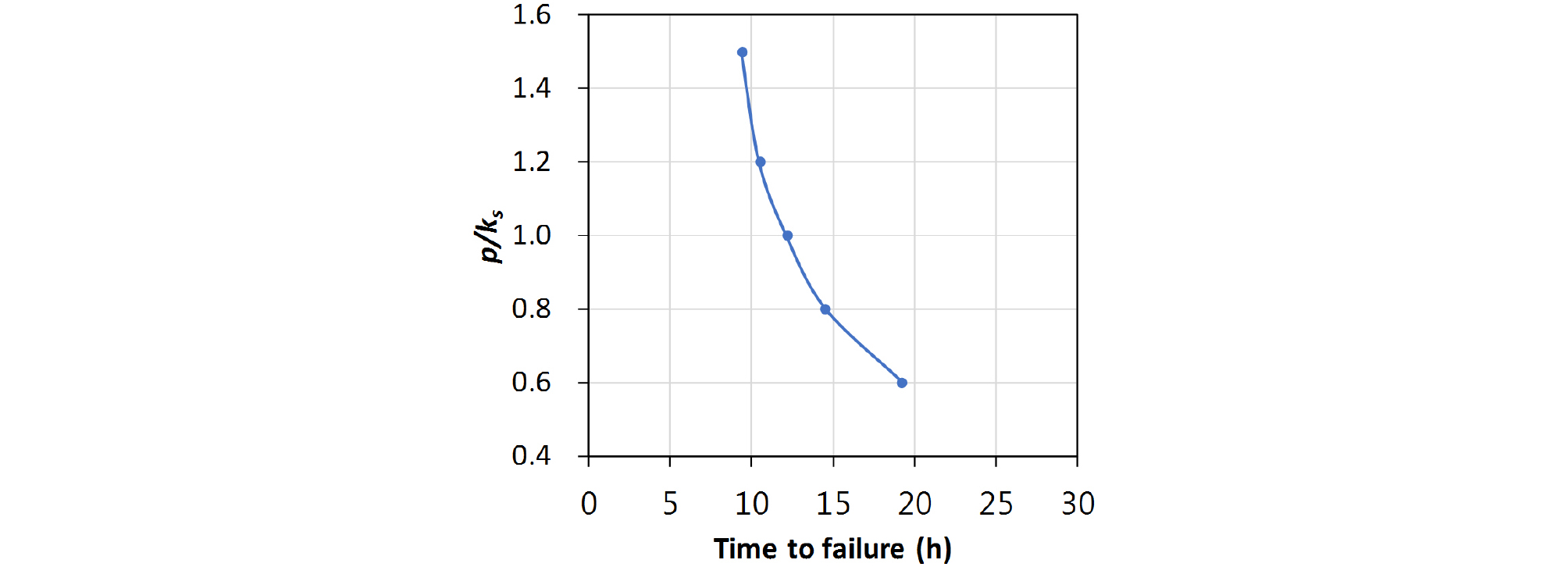
Fig. 6은 Fig. 5의 결과로부터 안전율이 1.0 이하로 감소하여 사면파괴가 발생하는 시간을 p/ks에 따라 나타낸 것이다. 즉, Fig. 6은 강우강도에 따른 사면 파괴시간의 관계를 결정론적 해석으로부터 구한 것이다. 강우강도가 커질수록 파괴에 소요되는 시간이 감소하지만 어느 수준 이상의 강우강도에서는 그 영향이 점차 감소함을 알 수 있다.
5.3 확률론적 해석
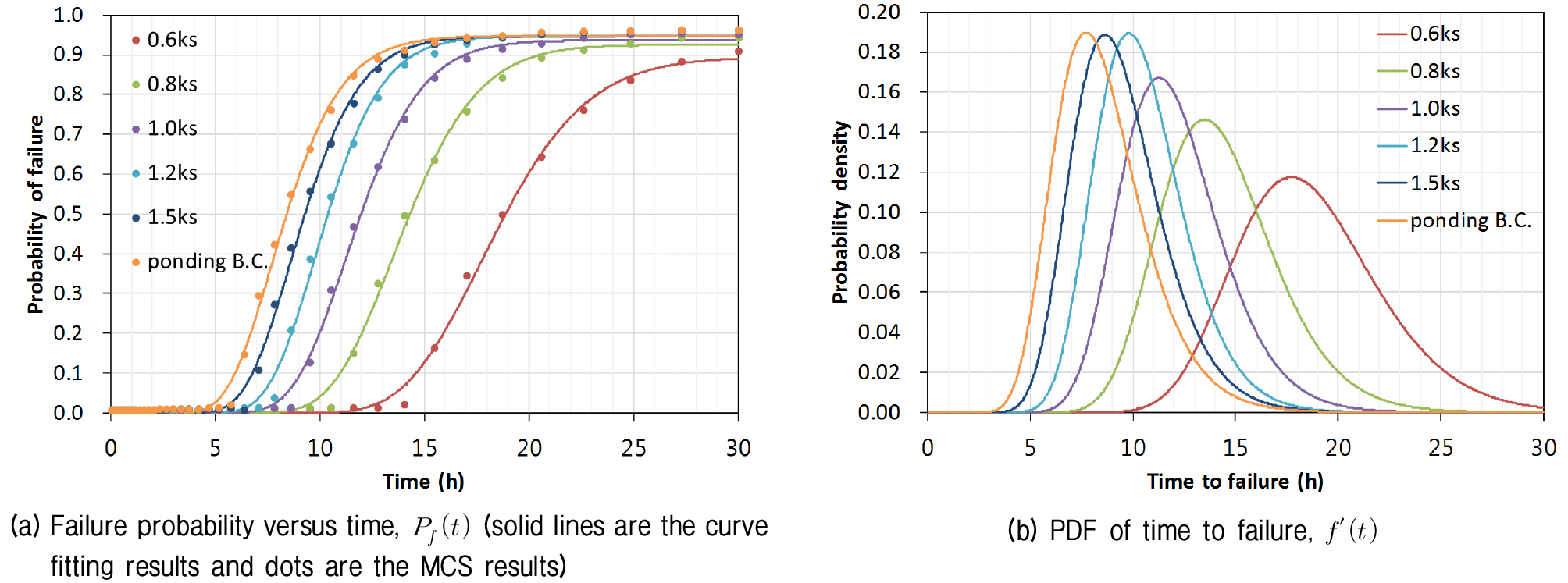
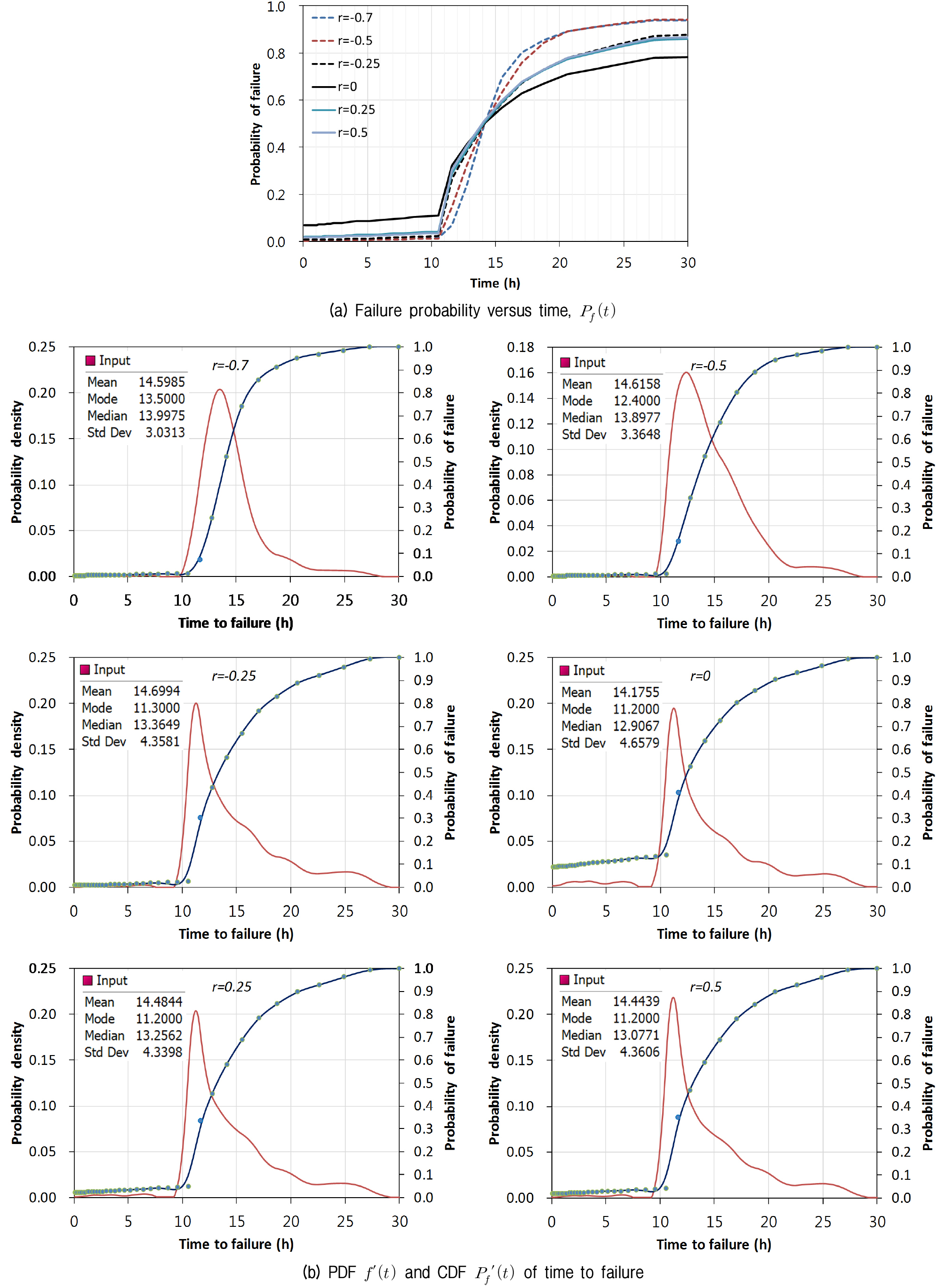
지반의 전단강도 정수를 랜덤 변수로 고려하여 강우의 침투에 대한 확률론적 사면 안정해석을 수행하였다. 이를 위해 Table 1에 제시된 전단강도 정수의 통계학적 자료를 사용하였다. MCS로부터 확률론적 거동을 구하기 위해 임의의 시간 단계에 대해 50,000회의 사면 안정해석을 수행함으로써 강우의 지속 시간에 따른 파괴확률을 구하였다. 강우의 침투에 의한 간극수압의 분포를 확률론적 사면 안정 해석의 입력값으로 사용하였다. 시간에 따른 사면의 파괴확률을 나타내는 취약도 곡선은 Fig. 7(a)와 같이 식 (12)의 대수정규분포의 CDF로 곡선맞춤 되었다. 이를 위해 임의의 시간 단계에서 MCS 수행 중 한계상태를 초과하는 빈도로부터 계산된 파괴확률(Fig. 7(a)의 점으로 표시)을 기반으로 Matlab의 최적화기법을 이용하여 관측값과 이론값의 평균 제곱 오차(mean square error)가 최소가 되도록 곡선맞춤을 수행하였다. 곡선맞춤에 의해 구해진 대수정규분포 CDF의 변수와 파괴시간의 측정 척도들은 Table 2와 같다.
Table 2. Results of curve fitting and calculated summary measures of reliability
강우의 초기에는 침투 깊이가 얕아 깊은 곳에 형성되는 임계 파괴면에서 계산되는 안전율에 강우의 침투가 큰 영향을 미치지 못한다. 따라서 초기의 파괴확률은 매우 작은 값을 보이나 침투가 진행함에 따라 파괴확률은 증가하고 충분한 시간 동안 강우가 지속되면 일정한 파괴확률로 수렴하는 경향을 보인다. 강우 강도가 증가할수록 침투가 빨리 진행하므로 파괴확률이 증가하는 시간이 짧아지고 시간에 따른 파괴확률 곡선의 경사가 급해지나 강우강도가 커질수록 그 효과는 점점 줄어든다(Fig. 7(a)). USACE(1997)에서 제시한 지반구조물의 기대 성능수준에 따른 파괴확률의 관계(Table 3)를 활용하여 Fig. 7(a)로부터 시간에 따른 비탈면의 성능수준을 평가할 수 있다. 식 (6)으로부터 시간에 대한 취약도 곡선의 기울기는 MCS에서 수행된 모든 해석의 수를 기준으로 한 파괴 시간의 확률밀도를 나타낸다. 확률밀도함수 f(t)는 강우의 침투에 의한 파괴가 발생하지 않은 해석의 경우도 포함하므로 파괴분포 분석을 위해서는 파괴된 경우만을 고려한 시간에 따른 확률밀도함수 f'(t)를 구해야 한다. f'(t)는 시간에 따른 파괴의 분포를 나타냄으로써 강우지속 시간에 따라 파괴가 발생할 가능성이 어느 정도인지를 보여준다.
Table 3. USACE (1997) guidelines for probability of failure in geotechnical and infrastructure projects
| Expected performance level | Probability of unsatisfactory performance |
|
High Good Above average Below average Poor Unsatisfactory Hazardous |
0.0000003 0.00003 0.001 0.006 0.023 0.07 0.16 |
시간에 따른 사면파괴의 분포는 Fig. 7(b)와 같이 대수정규분포의 PDF에 의해 나타낼 수 있다. Fig. 7(b)의 각 곡선의 정점은 MCS에서 가장 많은 파괴가 관찰된 시점, 즉 가장 파괴의 발생 가능성이 높은 시점인 tmode(파괴시간의 최빈값)에 대응하는 점이다. 강우강도가 증가할수록 PDF곡선은 점점 좁고 높아지면서 좌측으로 이동하는 경향을 보였다. 이러한 경향은 강우강도가 커질수록 사면파괴가 짧은 강우의 지속시간 후에 대부분 발생하게 됨을 의미한다. 반대로 강우강도가 작을수록 사면파괴가 발생하기에 필요한 지속시간이 길어지고, 더 긴 기간에 걸쳐 발생하게 됨을 의미한다.
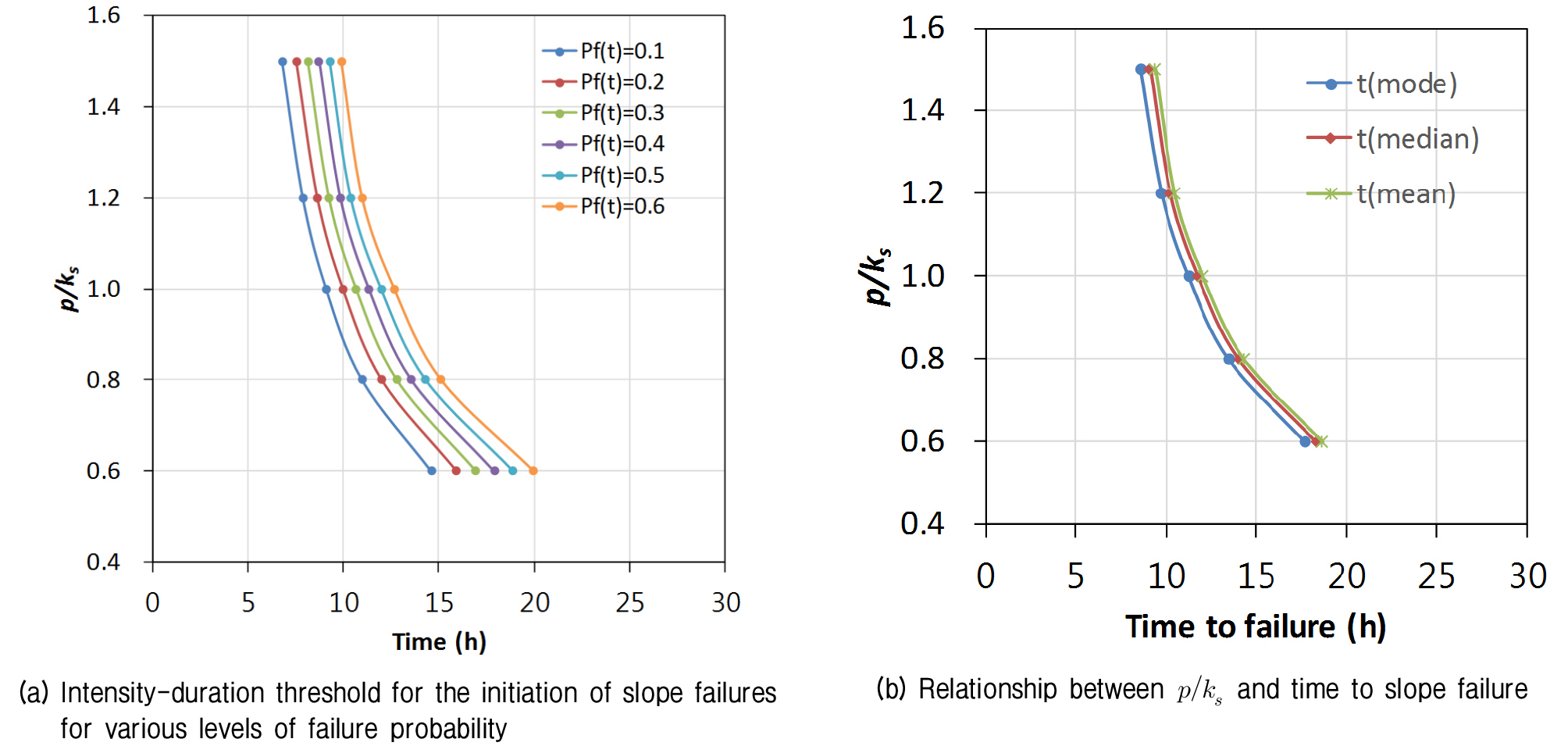
Fig. 7(a)의 취약도 곡선으로부터 주어진 강우강도에서 다양한 파괴확률 수준에 도달하기 위하여 필요한 강우 지속시간을 결정할 수 있다. Fig. 8(a)는 다양한 수준의 파괴확률에 도달하기 위해 요구되는 강우강도-지속시간의 관계를 나타낸다.
강우의 침투에 의해 사면이 파괴에 도달하기 위한 시간도 역시 불확실성을 포함하는 랜덤 변수이므로 Fig. 8(b)와 같이 파괴시간을 대표하기 위한 척도로 평균, 중앙값 및 최빈값을 사용하였다. 주어진 강우강도에 대하여 사면 파괴가 발생하는데 필요한 시간은 평균인 tmean에 의해 가장 길게 평가되고 최빈값인 tmode가 가장 짧게 평가되었다. 즉, tmode가 tmean이나 tmed에 비하여 보수적인 지속시간을 예측한다. Fig. 8(b)는 지반의 전단강도의 불확실성을 고려했을 때 강우에 의한 사면 파괴의 발생을 예측할 수 있도록 확률론적 해석에 의한 취약도 곡선으로부터 유도된 임계 강우강도-지속시간의 관계를 나타낸다.
램덤 변수로 고려되는 점착력과 내부마찰각의 교차 상관계수가 확률론적 해석 결과에 미치는 영향을 살펴보기 위해 다른 조건은 그대로 유지한 채, 상관계수를 -0.7≤r≤0.5의 범위에서 변화시키며 강우강도 조건이 p/ks=0.8인 경우에 대하여 해석을 실시하여 취약도 곡선을 작성하였다. Fig. 9(a)는 상관계수를 변화시켰을 때 시간에 따른 사면의 파괴확률을 나타낸 것이다. 초기의 작은 파괴확률은 깊은 파괴면과 관련되며 이에 해당하는 파괴확률은 상관계수가 0인 경우에 매우 크게 나타났으나 30시간 경과 후의 파괴확률은 가장 작게 예측되었다. 큰 음의 상관계수를 가질수록 초기 파괴확률이 작았으나 30시간 후에는 가장 큰 파괴확률을 나타내었다.
취약도 곡선을 특정 확률분포로 표현하기 어려운 경우에 대하여 파괴분포 해석을 수행하기 위해서 Fig. 9(a)의 취약도 곡선을 Matlab Curve Fitting Toolbox의 smoothing spline model을 이용하여 곡선맞춤을 수행하였다. 곡선맞춤으로 얻어진 시간에 따른 취약도 곡선을 ‘differentiate’함수를 사용하여 시간에 대하여 미분함으로써 사면파괴시간의 PDF를 구하였다. Fig. 9(b)는 상관계수에 따른 취약도 곡선의 곡선맞춤으로부터 구한 사면파괴 시간의 CDF Pf'(t)와 PDF f'(t)의 결과를 나타낸다. 사면파괴까지의 시간의 평균, 중앙값 및 최빈값은 f'(t)로부터 평가할 수 있다.
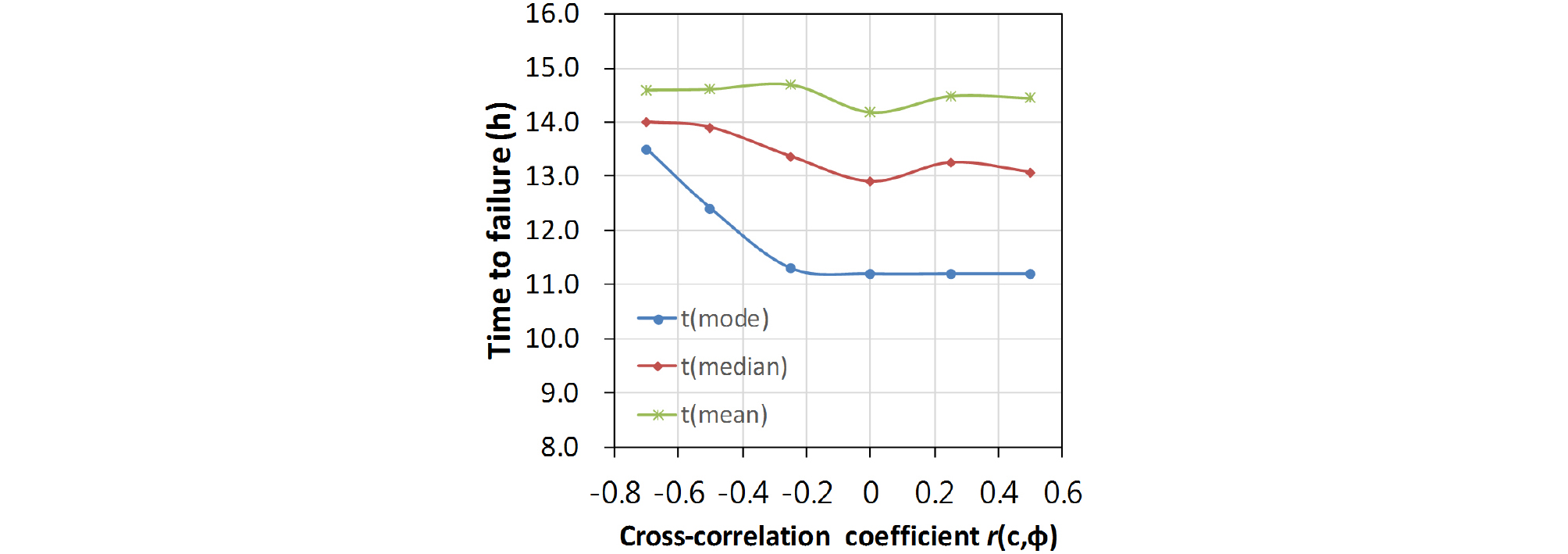
Fig. 10은 평가된 사면파괴 시간의 평균, 중앙값 및 최빈값을 상관계수에 따라 나타낸 것이다. 사면파괴의 평균값은 상관계수에 따라 큰 변동이 없으나 최빈값은 음의 상관계수 영역에서 큰 영향을 받는 것으로 보인다.
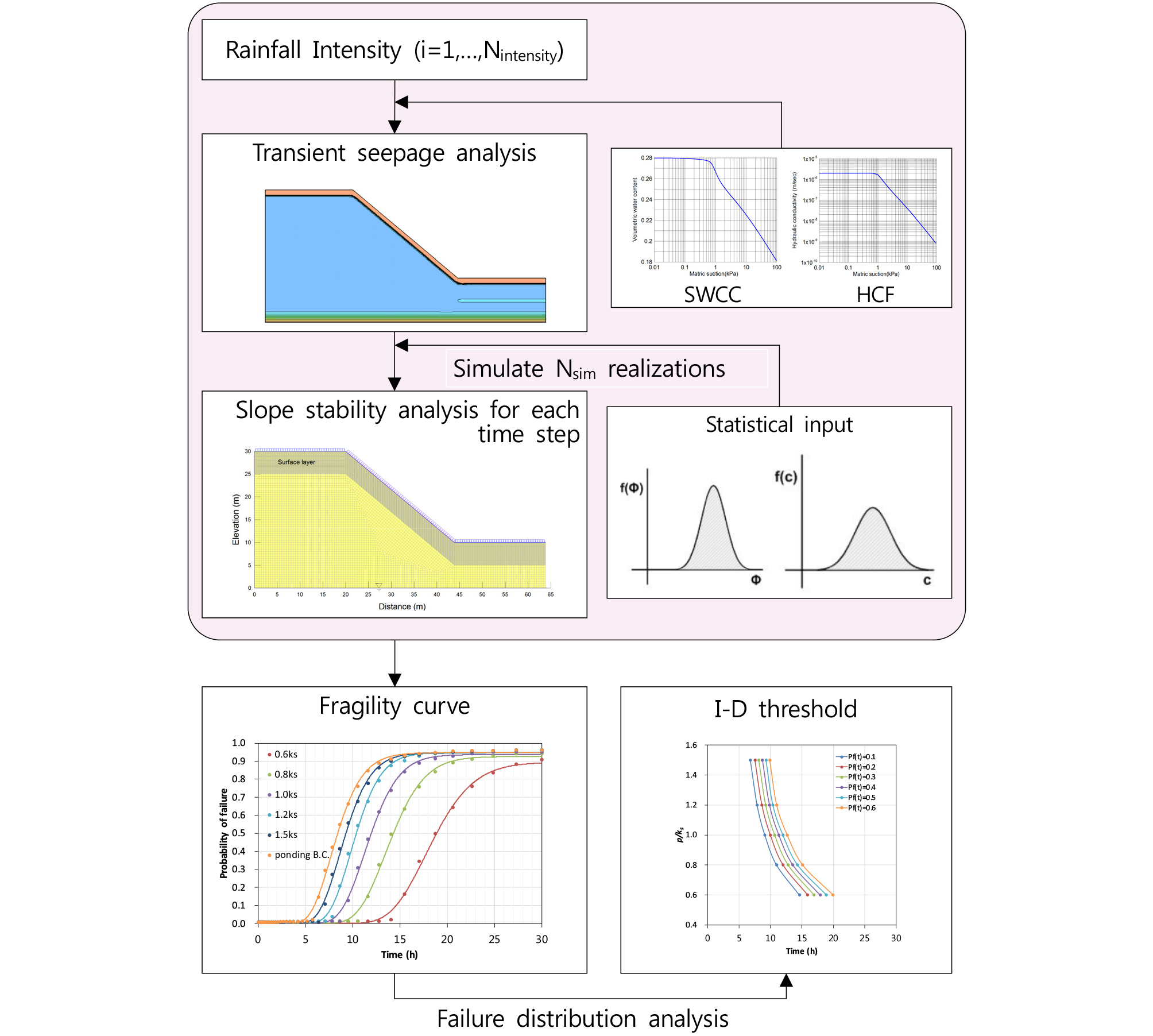
Fig. 11은 불확실성에 따른 사면의 취약도 곡선 작성 및 파괴분포 분석 절차를 단계별로 보여주는 모식도이다.
6. 결 론
강우강도와 지속 시간에 의한 강수량 정보는 다양한 기반 시설물의 설계, 운영 및 유지 관리에 중요한 요소로 여겨져 왔다. 따라서 효율적인 사면재난 관리를 위해서는 강우 강도와 지속 시간의 함수로 표현되는 사면의 취약도 곡선으로부터 사면파괴를 예측하고 사면의 파괴시간을 확률적으로 예측할 수 있는 방법이 필요하다.
본 연구에서는 강우의 침투에 따른 토사사면의 파괴에 대한 강우강도-지속시간의 강우기준을 평가하기 위하여 수치해석에 의한 파괴시간의 확률론적 해석 절차를 제안하였다. 이 절차는 지반의 강도정수의 불확실성을 고려하는 MCS에 의한 확률론적 사면 안정해석의 결과에 기초하여 사면 파괴 발생 시간을 확률적으로 분석한다. 연구로부터 다음과 같은 결론을 얻었다.
(1) 시간 의존적인 사면의 파괴 과정을 분석하기 위해서는 사면의 파괴확률이 시간에 대하여 연속적인 형태로 표현되어야 한다. MCS에 의한 사면의 파괴확률은 임의의 시간 단계에 대해서만 구해지므로 시간에 대하여 연속적인 형태로 표현하여야 한다. 본 연구에서 사용된 대수정규 확률분포와 smoothing spline 모델은 다소의 오차를 포함하나 대체로 사면의 파괴분포를 효과적으로 나타낼 수 있음을 보여준다. 이 방법들을 사용하면 확률론적 해석을 수행하는 데 필요한 시간 단계 수를 줄일 수 있으므로 확률론적 해석에 소요되는 시간을 줄임으로써 사면 파괴과정을 효율적으로 분석할 수 있다.
(2) 그 동안 사면의 파괴시간은 결정론적으로 평가되어져 왔다. 그러나 강우 시 사면이 파괴되기까지의 시간은 불확실성을 포함한 무작위 변수이다. 따라서 평균 파괴 시간, 파괴 시간의 중앙값 및 최빈값과 같이 신뢰성을 측정할 수 있는 다양한 척도를 결정할 수 있다. 제안된 파괴분포 분석 절차를 사용하여 강우 강도와 사면파괴 시간 사이의 관계를 나타내는 도표를 작성할 수 있다. 이 관계는 지반강도 특성의 불확실성을 고려할 때 사면 파괴가 발생하기 위한 일종의 강우강도-지속시간의 임계값이다.
(3) 사면 파괴 발생 과정의 복잡성으로 인하여 사면 파괴의 발생 예측에는 많은 불확실성이 연관되어 있다. 따라서 제안된 방법에 대한 추가 연구가 필요하지만 제안된 방법은 사면 파괴 발생 가능성 평가에 대한 통찰력을 제공할 수 있다.