1. 서 론

암반내의 불연속면은 다양한 원인으로 생성되며, 안정성에 관련된 대부분의 공학적 문제는 암반내에 발달하고 있는 불연속면의 기하학적 형성과 공간적 분포에 의하여 결정된다(Jaeger et al., 2007). 암반공학에서 불연속면은 균열(fissure), 절리(joint), 단층(fault) 그리고 층리(bedding plane) 등의 다양한 형태로 존재하지만, 일반적으로 ‘절리(joint)’가 암반내의 불연속적인 특징인 약한 평면을 통칭하는 용어로 사용된다(Cai and Horii, 1992). 이러한 절리면은 암반의 역학적 변형을 지배할 뿐만 아니라 암반 내부를 흐르는 지하수나 유체의 수리학적 통로 역할을 하게 된다.

일반적인 현장조사는 암반내 절리면의 간격(spacing), 연속성(persistence) 그리고 방향(orientation) 등을 파악한다. 지중이나 일부 지표에서 제한적으로 수집된 절리들에 대한 정보를 기준으로 통계적인 방법을 이용하여 지중 절리의 공간적인 분포를 산정하게 된다(Lei, 2016). 이러한 절리의 불확실성과 변동성은 절리를 포함된 암반의 공학적 설계를 어렵게 한다. 또한 암반내 절리의 간격과 구조물의 상대적인 크기가 유사한 경우(Barton et al., 2001), 절리와 구조물의 상대적인 위치가 구조물의 안정성 평가에 매우 중요하다. 즉, 통계적 방법으로 생성된 절리를 이용한 수치해석 결과는 상당한 변동성을 갖을 뿐만 아니라(Brideau et al., 2012), 절리의 공간적 분포가 동일하더라도, 구조물과의 상대적인 위치에 따라 해석결과들의 차이가 크게 발생할 수 있다. 따라서 구조물과 절리의 공간적 분포에서 상대적인 위치에 따른 변동성을 고려한 암반의 결정론적 연구가 필요하다.

실무에서 암반사면의 안정성 검토는 암반내 절리에 대한 지질조사를 시작으로 평사투영망을 이용한 운동학적 해석과 한계평형 해석을 수행한다. 기존의 수치 모델링 기법은 크게 연속체 해석법(FEM, FDM 등)과 불연속체 해석법(DEM, DDM 등)으로 구분할 수 있다(Stead et al., 2006). 연속체 해석법은 절리를 포함한 암반의 기하학적 형상을 단순화하는 대신 복잡한 등가의 역학적 구성모델(Equivalent mechanical constitutive model)을 요구한다(Sitharam et al., 2001; Son et al., 2014). 반면 불연속체 해석법은 절리에 의하여 분리된 온전한 암석(intact rock)과 절리들에 대한 직접적인 모델링이 가능하지만, 해석 범위가 넓거나 3차원 암반사면 해석에는 적용이 제한되고 지하수 흐름과 연계해석이 어렵다.

이러한 문제를 해결하기 위하여 규칙적인 절리를 포함한 암반의 역학적 해석하기 위한 내제적 절리-연속체 모델(Implicit joint-continuum model)을 제안되었다. 이 모델은 연속체 내부의 절리군에 방향성, 간격 그리고 전단과 압축에 관한 변형특성 등을 반영하여, 온전한 암석과 다양한 절리군의 변형특성을 동시에 고려할 수 있다. Amadei and Goodman(1981) 이후로 역학적 컴플라이언스 텐서(Compliance tensor) 사용하여 절리군의 기하학적 형상을 고려할수 있는 이방성 구성 모델에 대한 연구가 지속되었다(Agharazi et al., 2012; Bagheri and Settari, 2006; Cai and Horii, 1992; Gan and Elsworth, 2016; Grujovic et al., 2013; Huang et al., 1995; Maghous et al., 2008; Oda, 1986; Rafeh et al., 2015; Samadhiya et al., 2008; Wang and Huang, 2009). 이러한 지속적인 연구에도 불구하고, 일반적인 절리군의 특성을 고려하면서 암반의 변형에 대한 이론식과 일치하는 탄성 컴플라이언스 텐서는 제시되지 않았다. 하지만, 최근 Shin and Santamarina(2019)는 일반적인 절리군에 대한 이론적인 변형특성과 일치하고, 절리면의 탄소성 변형 특성도 모사할수 있는 암반의 역학적 컴플라이언스를 제시하였다. 그리고 절리군을 포함된 암반의 수리-역학적 연계해석 통하여 열적, 화학적 연계해석을 수행할수 있는 방법을 제시하였다.

본 논문에서는 Shin and Santamarina(2019)이 제시한 임의의 방향과 간격의 절리군을 포함한 암반의 역학적 컴플라이언스 기반의 3차원 내재적 절리-연속체 모델을 설명하고, 암반사면의 평면파괴 가능성 평가에 이용되는 Daylight envelope에 대한 수치해석적 검증을 수행하고자 한다.

2. 내재적 절리-연속체 모델

2.1 다중규모 계층적 절리 모델링

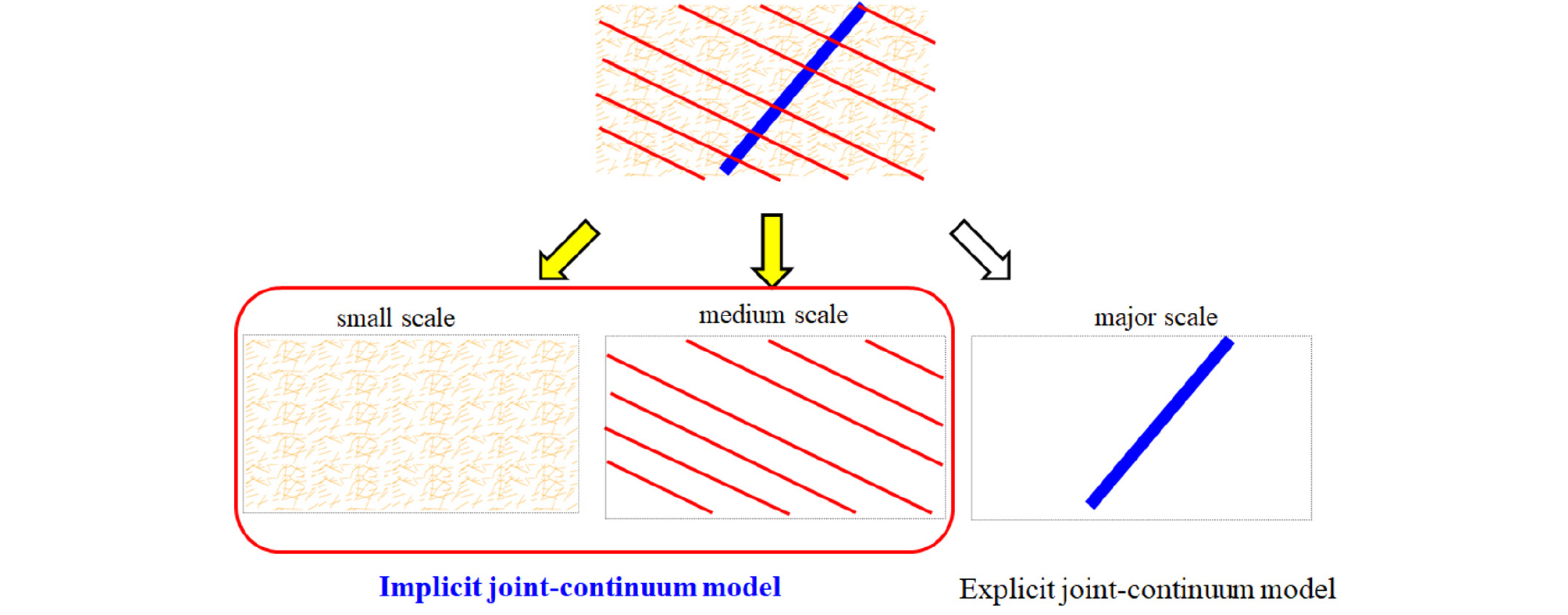
자연적인 암반은 미세균열, 절리 그리고 단층으로 크게 구분할수 있는 계층적인 불연속성을 갖는다. 암반에 포함한 불연속면들의 이러한 계층적 구조는 상호작용을 하면서 암반의 수리-역학적 거동을 지배한다. 하지만 한가지의 모델을 이용하여 모든 계층적 구조를 모사하기 어렵기 때문에 암반의 공학적 특성을 효과적으로 재현하기 위하여 다중규모 계층적 절리 모델링(Multiscale hierarchical fracture modeling)이 제시되었다(Lee et al., 2001; Pluimers, 2015). 계층적 구조의 각 단계에서 불연속면의 특징은 연속체로 모델링된다(Liu et al., 2018).

본 논문에서는 다양한 규모의 불연속면을 포함한 일반적인 암반을 모델링하기 위하여 Fig. 1과 같은 3단계의 계층적 구조를 설정하였다. 1) 대규모(major scale) 불연속면은 계층적 구조의 최상위에 있으며, 단층과 같이 숫자가 적어 외재적인(explicit) 방법으로 모델링할 수 있다(Goodman et al., 1968; Desai et al., 1984). 2) 소규모(small scale) 불연속면은 다수의 불연속적인 균열로 탄성 컴플라이언스 텐서(Oda, 1986)에 의한 등가 연속체 모델(equivalent continuum models)로 해석할 수 있다. 3) 중간규모(medium scale) 불연속면은 불연속면의 간격과 방향이 일정하면서 연속성이 있는 정규화된 기하학적 구조를 갖는 절리군으로, 2.1절에서 제시한 내재적 절리-연속체 모델(implicit joint-continuum model)을 이용하여 모델링한다.

Fig. 1

Multi-scale hierarchical approach for fractured rock mass

2.2 내재적 절리-연속체 모델의 수식화

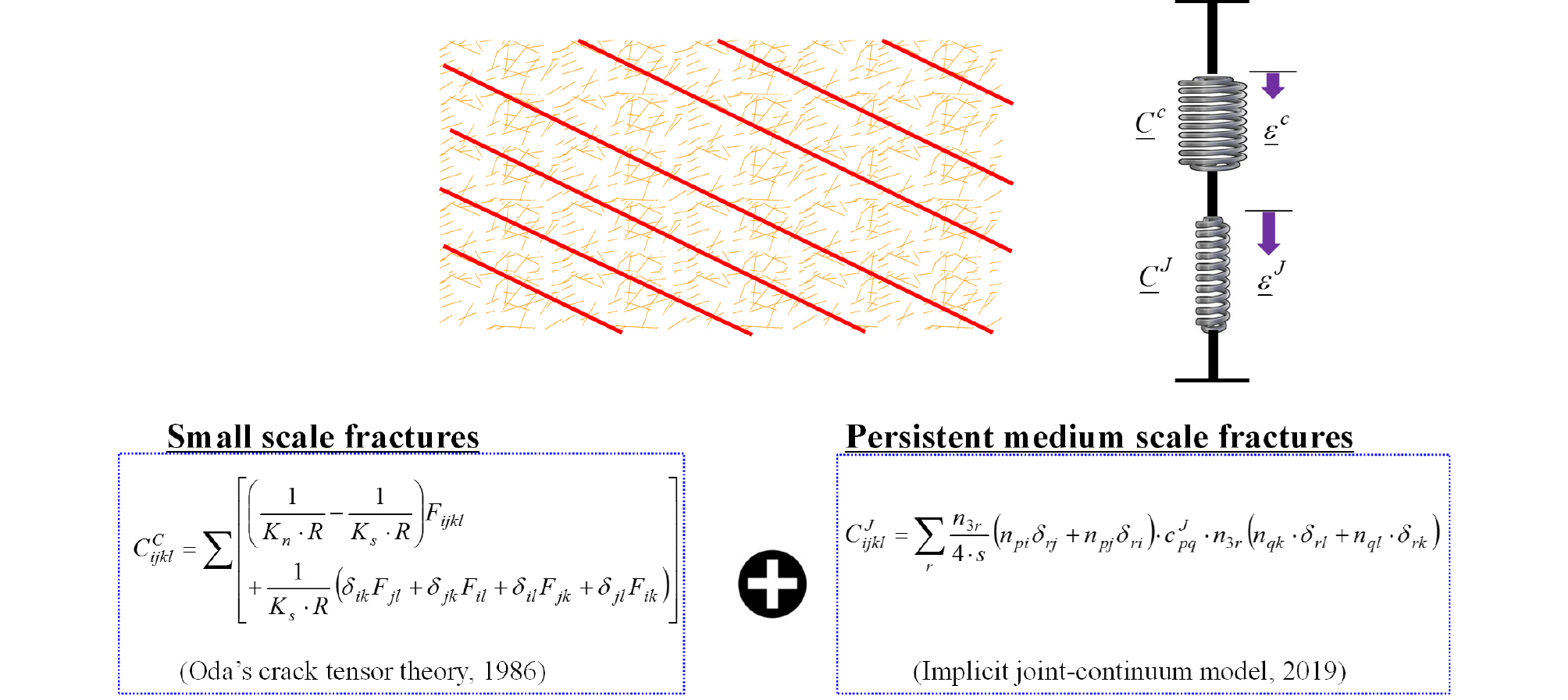
절리군(joint set)은 평면 형상, 규칙적인 간격 그리고 동일한 방향성을 갖는 체계적인 절리(systematic joints)의 특성을 보이는 인접한 다수의 절리들의 집합이다(Twiss and Moores, 2007). 내재적 절리-연속체 개념은 온전한 암석(소규모의 불연속적 절리 포함)과 절리군들의 역학적 특성을 동시에 갖는 단일 매체의 모델링 기법이며, 절리군의 영향은 모델 수식화에서 내제적으로 고려한다. Fig. 2a는 연속성을 갖는 절리군을 포함한 암반에서 절리의 주향(strike, θ)은 절리면과 X-Y 평면의 교차선과 북쪽 방향 (+Y) 사이의 시계 방향 각도로 정의된다. 경사각(dip angle, β)은 절리면과 X-Y 평면으로 형성되는 가장 가파른 각도이다. 따라서 3 개의 국부 단위 벡터는 절리면의 주향(θ)과 경사(β)로 정의 할 수 있다: 경사방향(dip direction) n₁ = (cosθ·cosβ, -sinθ·cosβ, -sinβ), 주향방향(strike direction) n₂ = (sinθ, cosθ, 0), 절리면의 법선 n₃ = (cosθ·sinβ, -sinθ·sinβ, cosβ). 절리의 간격 s는 절리군내의 인접한 두 절리의 직교 거리이다.

절리를 포함한 암반에 응력이 가해지면 온전한 암석과 절리군에 변형이 동시에 발생한다. 암반에 유발된 전체 변형률(ε)은 절리에서의 변형률(ε^J)과 온전한 암석의 변형률(ε^C)의 합이다(Fig. 2b). 온전한 암석과 절리에 대한 응력의 연속성으로부터, 암반의 역학적 거동은 온전한 암석과 절리군의 연속적 강성 시스템(serial stiffness system)으로 모델링할 수 있다. 외부응력 σ에 의하여 온전한 암석과 절리에 발생되는 변형률은 다음과 같은 컴플라이언스 텐서로부터 계산할 수 있다.

Fig. 2

Modeling a joint rock mass and definitions. (a) Coordinate system and joint orientation, (b) Schematic model for a jointed rock mass

여기에서 C^C와 C^J는 온전한 암석과 절리군의 컴플라인스 텐서(compliance tensor)이다.

암반내 절리군의 컴플라이언스 텐서(C^J)는 외부응력 σ에 의한 절리면에서의 상대 변위(u_i)와 이로부터 계산되는 절리면의 변형률(ε^J)로부터 결정된다. 암반내에 포함된 절리군의 컴플라인스는 전역좌표계 각각의 축에 직교한 면에 작용하는 응력에 의한 압축성의 합으로 산정할 수 있다. 전역좌표계 Z축에 직교하는 평면에 작용하는 응력을 σ_zi로 표시하면, 절리면에 작용하는 응력성분 S_q은 작용하는 응력과 절리면의 방향성으로 부터 S_q = n₃₃·σ_zi·n_qi이 된다. 모멘트 보존법칙에 의한 응력의 대칭성으로부터 Z축에 직교하는 평면에 작용하는 응력에 의한 절리면 내부의 응력 S_q은 다음과 같다.

여기서 σ는 2계 응력텐서 σ_ij이며, δ_ij는 Kronecker delta이다.

절리면의 응력-상대변위는 관계는 S_q = d^J_pq·u_q와 같은 탄소성 강성 행렬로 표현할 수 있다. 그리고 절리면에 대한 강성 매트릭스(d^J_pq)는 컴플라이언스 매트릭스(c^J_pq)와 역의 관계에 있다(c^J_pq = d^J_pq^-1). 식 (2)와 절리의 컴플라이언스 매트릭스(c^J_pq)로부터, 전역좌표계 Z축에 대한 절리면의 상대변위 u_q와 외부응력 σ의 관계는 다음과 같다.

전역좌표계에서 각 축에 대한 절리간격 s_i는 (s_ieⁱ)·n^z = s과 같고, Z 방향에 대한 절리의 간격은 s_Z = s/n₃₃이다.

Z축에 직교하는 평면에 작용하는 응력에 의한 절리면의 국부 변위(u_q)는 전역좌표계에서 변형률 텐서(ε^J_ij)로 부터 산정할 수 있다. 먼저, 절리면의 국부 변위량 으로부터 Z축에 직교하는 평면의 단위 길이당 암반의 전역 변위(U_i = u_k·n_ki/s_Z)를 산정할 수 있다. 그리고, Z 평면에 대한 전역 변위로부터 전역 변형률을 계산할 수 있다(ε^J_ZZ = U_Z, γ^J_ZX = U_X, γ^J_ZY = U_Y). 연속체 역학에서 변형률 텐서에 대한 대칭성의 원리에 의하여 변형률 ε^J_ij은 다음과 같다(Oda, 1986).

식 (3)과 식 (4)로부터 전역좌표계 Z 방향에 대하여 절리군에 대한 외부응력(σ)과 변형률(ε^J_ij)의 관계를 정의할 수 있다. X와 Y 방향에 대한 컴플라이언스 텐서도 동일한 방법으로 계산할 수 있다. 암반내 절리군의 컴플라이언스 텐서는 각 전역좌표계의 합으므로 단일 절리군에 대한 컴플라이언스 텐서(C^J)는 다음과 같다.

여기서 C^J는 암반내 절리군의 변형에 대한 4계 컴플라이언스 텐서이다(C^J_ijkl).

Fig. 3에서 소규모의 불연속적 절리는 Oda(1986)가 제시한 탄성 컴플라이언스 텐서를 이용하여 모델링할 수 있다. 최종적으로 여러개의 절리군을 포함한 암반에 대한 컴플라이언스 텐서 C^m는 각 절리군과 온전한 암석에 대한 컴플라이언스 텐서의 선형적인 합으로 계산할 수 있다(Fig. 3).

Fig. 3

Summation of compliance tensors for small-scale fracture and persistent medium-scale fracture in implicit joint-continuum model

절리를 포함한 암반의 강성 텐서(D^m)는 응력와 변형률의 관계를 결정하며(dσ = D^mdε), 이는 컴플라이언스 텐서(C^m)의 역으로 산정할 수 있다. 개발된 내재적 절리-연속체 요소는 토사와 암반의 다공질흐름에 대한 THMC해석을 위하여 개발된 Geo-COUS(Geo-COUpled Simulator) 유한요소 프로그램과 결합하였다.

3. 암반사면의 평면파괴 해석

암반사면의 붕괴는 일반적으로 평면(planar), 쐐기(wedge) 그리고 전도(toppling) 파괴로 구분하고 있다(Hoek and Bray, 1981). 평사 투영법(stereographic projection plots)을 이용하는 운동학적 해석(kinematic analysis)에서 암반사면과 절리면의 상대적인 방향성(orientation)은 사면의 잠재적인 안정성을 평가하는 요소이다. 평면파괴가 발생하기 위해서는 절리면의 경사(β^J)는 암반사면의 경사(β^P)보다 작고 절리면의 마찰각(φ^J)보다는 커야 한다. 또한 절리면에 대한 극점(pole)이 사면의 daylight envelope내에 있으면서(Hoek and Bray, 1981; Lisle, 2004), 절리면과 암반사면의 경사방향 편차가 20°보다 작아야 한다 |θ^J - θ^P| < 20°(Hudson and Harrison, 2000).

암반사면의 평면파괴에 대하여 Daylight envelope을 이용한 경험적인 방법은 탈락한 암반 블록이 사면에 비스듬한 방향이 아닌 사면의 경사방향으로 이탈하는 경험적인 사례들로부터 결정되었다(Duncan and Christopher, 2010). 그리고 daylight envelope내의 측면 한계 20°는 평면파괴의 안정성 해석에 주로 사용되고 있지만, 이에 대한 이론적 혹은 수치해석적 연구는 전무하다(Duncan and Christopher, 2010; Goodman and Shi, 1985).

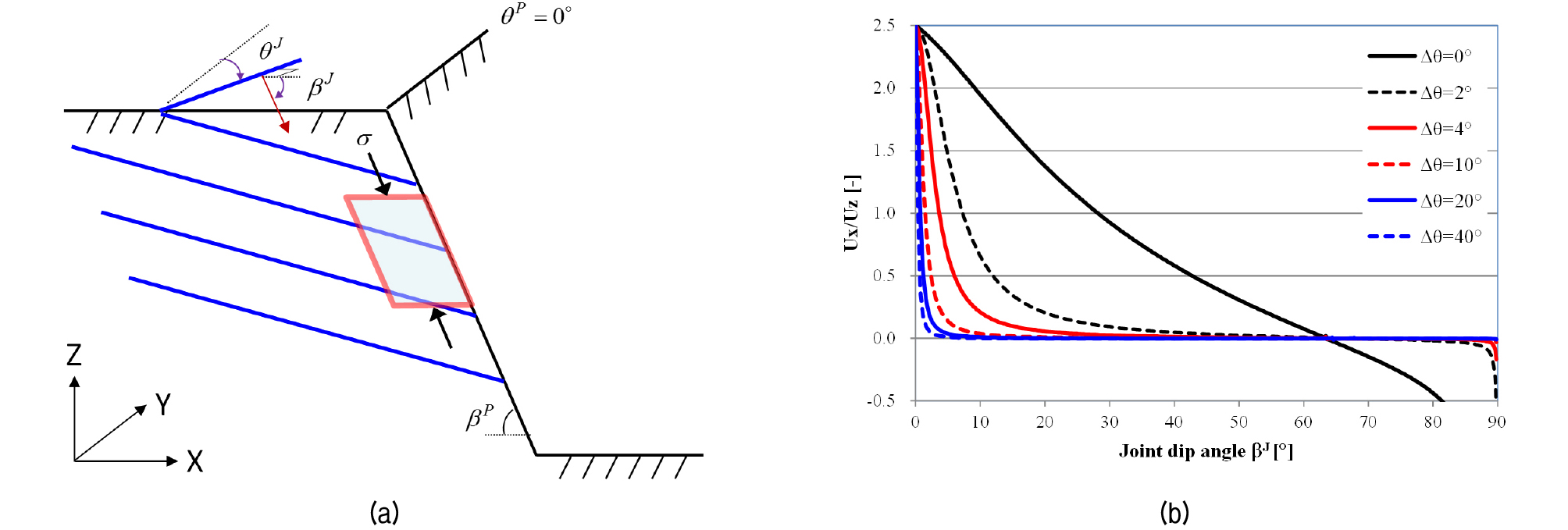
암반사면의 운동역학적 평면파괴 가능성에 대한 수치해석을 수행하였다. 암반 사면의 주향과 경사는 θ^P = 0°, β^P = 1:0.5(63°)이며, 암반내 절리군의 주향(θ^J)과 경사(β^J)에 대한 매개변수 해석을 수행하였다(Fig. 4a). 평면 변형률 해석조건에서 암반사면 부분을 32요소와 121개의 절점으로 모델링하고, 해석영역의 바닥부의 연직방향 변위을 억제하는 조건에서 사면의 자중을 재하하였다.

절리군의 주향(θ^J)과 경사(β^J)의 변화에 따른 사면 표면의 수평/연직 변위비(U_X / U_Z)를 수치해석으로 산정하였다(Fig. 4b). 암반사면과 절리면의 주향이 일치하는 경우(Δθ = θ^J - θ^P = 0°), U_X / U_Z는 β^J = 0°에서 최대값이며, β^J > β^P에서 음의 값으로 사면내부로 변위가 발생한다. 절리군과 암반의 작은 주향 편차(Δθ)도 U_X / U_Z을 크게 감소시키는 것으로 나타났다(Hoek and Londe, 1974). 각 주향에 대하여 임계 수평/연직 변위비(U_X / U_X|_Δθ=0°×10^-4)를 적용하여 운동학적 평면파괴 가능성을 판별하였다(Fig. 4b).

Fig. 4

Kinematic analysis for planar joint failure in rock slope (Intact rock: E^C = 10⁴ MPa, n = 0.3; Joint: K_n = 5×10³ MPa/m, k_r = 0.2, s = 0.5 m). (a) Model geometry for rock slope and a joint set, (b) Effect of joint orientation on displacement ratio

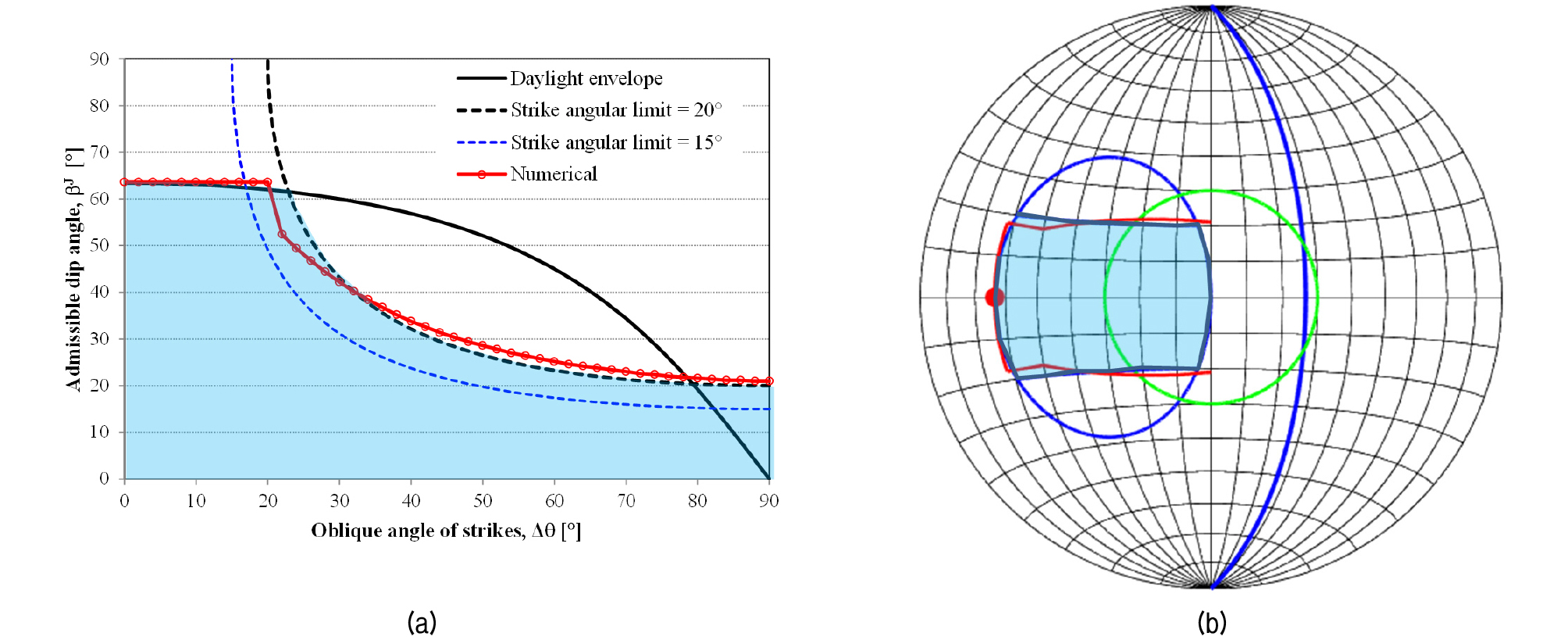
Fig. 5a는 Δθ의 변화에 따른 평면 파괴가 가능한 절리군의 경사를 나타내고 있으며, 실무에서 주로 사용하는 daylight envelope에 대한 편차각 |θ^J - θ^P| < 20°를 같이 도시하였다. 개발된 모델을 이용한 수치해석 결과(Fig. 5a의 빨간 실선)는 평사 투영법을 이용한 경험적인 방법(Fig. 5a의 검정 실선+점선=밝은 파랑색 영역)과 상당히 일치함을 알수 있다. 암반사면과 절리군의 주향편차 20°보다 작으면 수치해석 결과는 daylight envelope와 일치하고, 주향편차 30°이상에서는 daylight envelope내의 20° 측면 한계에 근접함을 알수 있다. 따라서 암반사면 평면파괴의 안정성 예비평가를 위하여 실무에서 사용하는 daylight envelope과 20° 측면 한계 설정이 적절한 것으로 판단된다. Fig. 5b는 Lambert 투영망에 암반사면의 평면파괴 가능성을 판단하는 측면 한계를 포함한 daylight envelope(Fig. 5b의 파란 실선)을 표시하고 있다. 암반사면의 평면파괴에 대하여 수치해석 결과(Fig. 5b의 빨간 실선)는 경험적인 방법과 상당히 일치함을 알수 있다. 본 연구는 기존의 경험적인 daylight envelope과 측면 한계에 대하여 처음으로 수치해석적 근거를 제시하였다.

Fig. 5

Kinematic analysis for planar joint failure in rock slope. (a) Admissible dip angle from empirical criterion and numerical simulation, (b) Stereographic projection of admissible planar failure from empirical and numerical results

4. 결 론

암반내의 절리는 암반의 전체적인 역학적 거동에 중요한 역할을 하고, 암반의 모델링은 내제된 절리로 인하여 매우 복잡한 수식화가 필요하다. 본 연구는 암반의 공학적 특성을 효과적으로 재현하기 위하여 다중규모 계층적 절리 모델링을 제시하였다. 단층과 같은 대규모 불연속면은 외재적인 모델링으로, 소규모의 불연속적 절리는 탄성 컴플라이언스 텐서를 이용하여 해석할 수 있다. 본 논문에서 제시한 내재적 절리-연속체 모델은 온전한 암석(소규모 불연속 절리 포함)과 절리군들을 연속적 강성 시스템으로 간주한다. 이를 바탕으로 절리군을 포함한 암반의 컴플라이언스 텐서는 온전한 암석과 각 절리군들의 컴플라이언스 텐서의 선형적인 합으로부터 산정하였다. 따라서 제시된 방법은 소규모 절리와 규칙적인 기하학적 구조를 갖는 중간규모 절리군을 동시에 모델링할 수 있다.

개발된 모델을 유한요소 프로그램에 탑재하여 암반사면의 평면파괴에 대한 경험적인 방법을 검증하였다. 암반사면의 평면파괴에 대하여 Daylight envelope을 이용한 경험적인 방법은 실무에서 안정성 해석을 위하여 주로 사용하지만, 이에 대한 이론적 혹은 수치해석적 근거는 부족하였다. 개발된 모델을 이용한 수치해석 결과는 암반사면의 평면파괴에 대하여 기존의 평사투영망을 이용한 경험적인 방법과 상당히 일치하고, daylight envelope과 20° 측면 한계 설정의 적정성을 확인하였다. 본 연구는 기존의 경험적인 daylight envelope과 측면 한계의 유효성을 수치해석적으로 증명하였다.

내재적 절리-연속체 모델은 연속체 기반으로 수식화므로 암반의 수리-역학적 연계해석 뿐만 아니라, 기존의 절리에 대한 열-수리-화학적 실험적 결과들을 실제 수치해석에 적용할수 있는 주요한 방법이 될수 있다.