1. 서 론
2. 이론적 배경
2.1 CPT를 통한 세립분 함량 예측
2.2 지반물성 예측의 불확실성
3. 결과 및 고찰
3.1 연구대상지
3.2 세립분 함량 예측식 적용성 분석
3.3 세립분 함량 예측 변동성 분석
4. 요약 및 결론
1. 서 론
액상화 현상(liquefaction)은 느슨한 포화 사질토 지반이 진동 하중을 받게 되면 순간적으로 과잉간극수압이 증가하여 지반은 전단강도를 거의 상실하게 되는 현상이다. 과거 지진피해를 살펴보면 액상화가 발생하는 경우 상부 구조물의 파괴나 부등침하, 측방유동, 제방붕괴 등에 의하여 경제적, 인명적으로 큰 피해가 발생하였다.
지금까지 액상화의 가능성을 평가하기 위한 수많은 연구들이 이루어져 오고 있으며, 가장 일반적으로 사용되는 평가방법은 응력기반 평가방법으로 지진에 의해 발생한 진동 전단응력비(cyclic stress ratio)와 흙의 저항 전단저항력비(cyclic resistance ratio)를 비교하는 방법이다(Idriss and Boulanger, 2008). 응력기반 평가방법은 일반적으로 표준관입시험(Standard Penetration Test, SPT)과 콘관입시험(Cone Penetration Test, CPT) 등 현장시험 결과로부터 저항 전단응력비를 산정한다. SPT 기반 액상화 평가는 Seed and Idriss(1971)에 의하여 처음 개발되었으며, 지금까지 SPT를 활용한 다양한 액상화 평가기법의 기반이 되고 있다. 국내에서는 Kim et al.(2000)이 Seed and Idriss의 방법을 수정 보완하여 국내 여건을 고려할 수 있는 액상화 평가법을 제안하였다. Boulanger and Idriss(2015)는 최근에 발생한 액상화 발생 사례를 추가하여 기존 상관관계를 보완하고 새로운 절차를 제시한 바 있다.
CPT 기반의 액상화 평가기법은 Zhou(1980)에 의하여 처음 제시되었으며, 이후 다양한 관련 연구들이 수행되었다(Olsen, 1997; Robertson and Wride, 1998; Idriss and Boulanger, 2008). CPT 기반 액상화 평가법은 연속적인 콘관입저항값을 이용하므로 층별 해석이 용이하며 CPT 결과로부터 다양한 지반 물성의 추정이 가능한 장점이 있다. 또한, SPT에 비하여 높은 정밀도를 제공하고 최근까지 액상화와 관련된 현장 데이터와의 상관관계에 대한 많은 데이터가 축적됨에 따라 그 사용이 증가하고 있는 추세이다(Bong and Kim, 2017).
액상화 평가법에서 흙의 저항 전단응력비를 산정할 때 중요한 입력 변수는 세립분 함량(#200체 통과중량 백분율)이다. 지반의 세립분 함량은 역학적 또는 수리학적 흙의 거동에 영향을 미치며, 액상화에 대한 흙의 저항력과 액상화 후 지반 침하 평가에 중요한 요소로 알려져 있다(Yi, 2014). Kim et al.(2008)은 세립분 함유량이 30% 이상이 되면 모래입자 사이의 세립분에 의한 효과가 약해짐과 동시에 입자끼리의 맞물림이 생기고 소성지수가 커짐에 따라 액상화 강도가 상승한다고 하였으며, Lee(2002)는 이방압밀 공시체의 경우 점토 함유량이 증가할수록 액상화 강도가 증가한다고 하였다. 또한, Bandini and Sathiskumar(2009)는 세립분 함량이 증가함에 따라 실트질 모래의 압축성이 증가하기 때문에 침하량 발생량이 증가할 수 있다고 하였다.
세립분 함량은 CPT 결과를 이용하여 예측할 수 있으며, CPT 기반 액상화 평가기법을 적용할 때 세립분 함량을 정확히 예측하는 것이 매우 중요하다. CPT 기반 세립분 예측식들은 1990년대 후반부터 제안되었는데, 일반적으로 흙의 거동 형태 지수(soil behavior type index, Ic)를 이용하여 세립분 함량을 예측한다. 그러나, 대상지반에 따라 Ic와 세립분 함량의 상관관계는 많은 차이가 존재하기 때문에 제안된 예측식들도 큰 차이가 발생할 수 있다. Idriss and Boulanger(2008)는 일반적으로 Ic와 세립분 함량과의 상관관계는 낮으며 예측 변동성이 크기 때문에 일반적으로 제안된 Ic와 세립분 함량의 상관관계를 사용하기보다 각 현장에 맞는 예측식을 개발하여 사용할 것을 추천하였다. 그러나, Ic는 세립분 함량뿐만 아니라 다른 다양한 지반조건에 의해 영향을 받기 때문에 현장의 지반조건에 가장 적합한 예측식을 선정하더라도 예측 오차에 대한 변동성은 매우 큰 것으로 알려져 있다. 그러므로, 세립분 함량 예측식의 변동성을 정량적으로 파악하여 세립분 함량 예측에 대한 신뢰구간을 파악하고 향후 신뢰성 해석을 위한 기초자료로 활용하는 것이 중요하다.
본 연구에서는 CPT 기반 세립분 함량 예측식에 대한 정확성 및 이에 따른 예측 변동성 분석을 수행하였다. 세립분 함량 예측식들은 다양한 지반조건에서 산정되었으므로 예측식에 따른 오차 및 변동성은 매우 크게 나타난다. 기존 세립분 함량 예측식에 대한 국내 적용성을 평가하고자 2017년 포항지진(규모 5.4)에서 액상화가 발생한 5개 지점에서 수행된 CPT 자료와 현장 세립분 함량 측정자료를 이용하여 기존 예측식들에 대한 예측 오차를 평가하였으며, 포항지역에 적합한 예측식을 선정하였다. 기존 예측식의 적용은 가장 낮은 예측 오차를 나타낸 예측식이라 하더라도 대상지역에 대한 토양특성을 반영하기에는 한계가 있으며, CPT를 통한 세립분 함량 예측은 많은 불확실성을 포함하고 있으므로 이에 대한 올바른 적용을 위해서는 예측값에 대한 신뢰범위를 정량적으로 평가할 필요가 있다. 그러므로, CPT 결과에 따른 지반 물성치의 고유 변동성을 파악하고 CPT의 측정오차, 예측식 사용에 따른 변환 불확실성을 추가적으로 고려하여 세립분 함량 예측에 대한 변동성을 평가하고 신뢰구간을 산정하였다.
2. 이론적 배경
2.1 CPT를 통한 세립분 함량 예측
흙의 거동 형태지수 Ic는 식 (1)을 이용하여 산정하며 세립분 함량과의 상관관계 도출에 이용된다(Robertson and Wride, 1998).
| $$I_c=\left[(3.47-\log Q_{tn})^2+\log F_R+1.22)^2\right]^{0.5}$$ | (1) |
식 (1)에서 Qtn은 정규화된 콘관입저항치이며, FR은 정규화된 마찰비로 다음 식들을 통하여 산정할 수 있다.
| $$Q_{tn}=\frac{(q_c-\sigma_{v0})}{P_a}\left(\frac{P_a}{\sigma_{v0}'}\right)^n$$ | (2) |
| $$F_R=\frac{f_s}{(q_c-\sigma_{v0})}\times100\%$$ | (3) |
여기서 qc와 fs는 CPT 결과에 따른 콘관입저항치와 주면마찰력이며, σv0, σv0', 그리고 Pa는 각각 연직 전응력, 연직 유효응력 그리고 대기압이다. n은 지반의 종류에 따라 결정되는 상수로 대략적으로 모래의 경우 0.5, 점토의 경우 1의 값을 갖는다.
Robertson and Wride(1998)는 CPT 결과가 세립분 함량 이외에도 여러 요인에 의하여 영향을 받기 때문에 겉보기 세립분 함량(FC, apparent fines content)이라는 용어를 사용하였다. 그리고, Ic와 세립분 함량 관측값의 상관관계를 분석하여 다음의 예측식을 제안하였다.
| $$FC=1.75I_c^{3.25}-3.7$$ | (4) |
만약, Ic가 1.64에서 2.36 사이이며 FR < 0.5%인 경우 세립분 함량 FC는 5%로 산정된다. Idriss and Boulanger(2008)는 Suzuki et al.(1998)에 의해 정리된 데이터를 활용하여 다음과 같은 예측식을 제안하였다.
| $$FC=2.8I_c^{2.6}$$ | (5) |
제안식의 형태는 Robertson and Wride(1998)가 제안한 식의 형태와 유사하며, 두 식 모두 Ic와 세립분 함량의 상관관계에 대한 비선형성을 반영하고 있다. Robinson et al.(2013)는 2011년 뉴질랜드 Christchurch에 발생한 지진자료를 이용하여 Ic와 세립분 함량의 상관관계 식을 다음과 같이 제안하였으며, 세립분 함량 예측식을 간단한 1차 함수의 형태로 나타내었다.
| $$FC=76.9I_c^{}-136.5$$ | (6) |
Boulanger and Idriss(2015)는 Suzuki et al.(1998)의 자료에 최근의 액상화 발생 자료들(e.g., Sancio 2003; Green et al., 2014; Cox et al., 2013)을 추가하여 다음과 같은 예측식을 도출하였으며, 기존 거듭제곱형태의 예측식(식 (5))을 1차 함수의 형태로 보정하였다.
| $$FC=80I_c^{}-137$$ | (7) |
이후, Stuedlein et al.(2016)은 Boulanger and Idriss(2015)가 Ic와 세립분 함량의 상관관계를 도출하기 위해 사용된 데이터에 미국 South Carolina의 Hollywood에 위치한 시험부지로부터 획득한 데이터를 추가하여 기존 예측식을 보정하였으며 다음과 같은 식을 제안하였다.
| $$FC=54I_c^{}-101$$ | (8) |
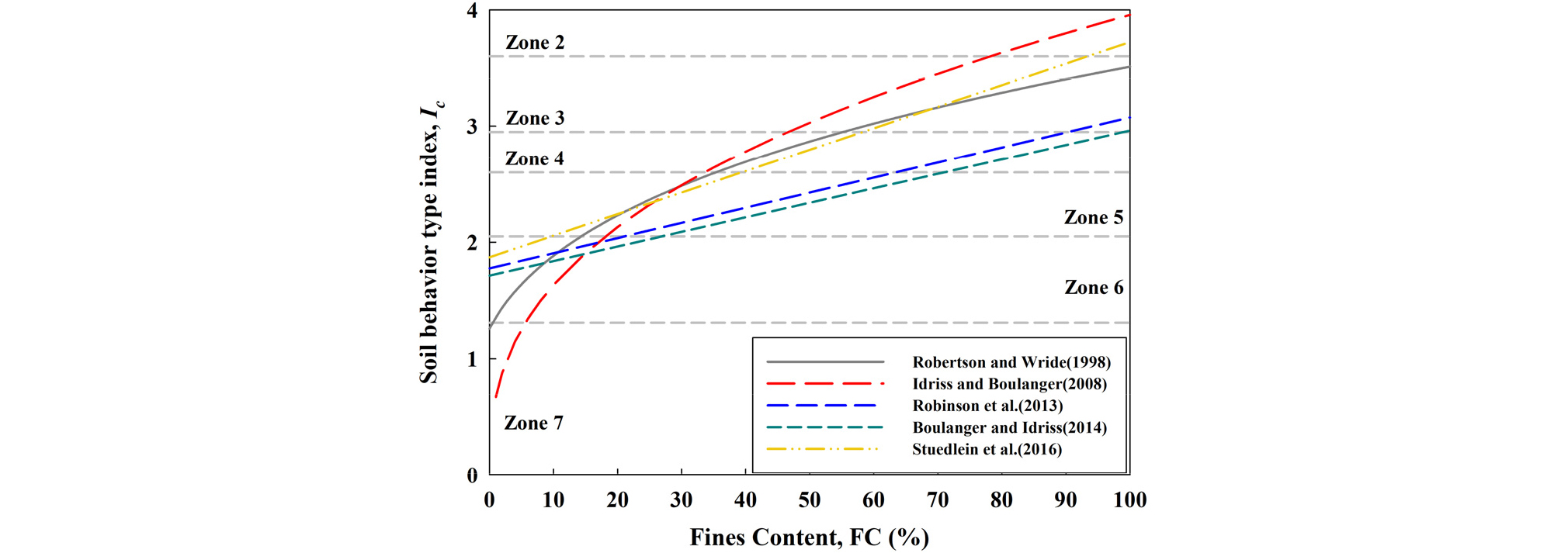
위에서 제안된 예측식들의 Ic와 세립분 함량 관계를 Fig. 1에 비교하였다. 여기서 Zone 2∼7은 Robertson(2010)에 의하여 제안된 Ic값의 범위에 따른 토층분류(Table 1)를 나타낸다. Robertson and Wride(1998)와 Idriss and Boulanger(2008)가 제안한 예측식은 Ic에 대한 거듭제곱형태로 비선형적 관계를 나타내고 있으며, 이후 연구자들에 의하여 제안된 3개의 예측식들은 모두 1차 함수로 식의 형태는 동일하며 상관관계를 도출하기 위하여 사용된 자료에 따라 기울기 및 절편에 차이가 존재하였다.
Table 1. Boundaries of soil behaviour type
2.2 지반물성 예측의 불확실성
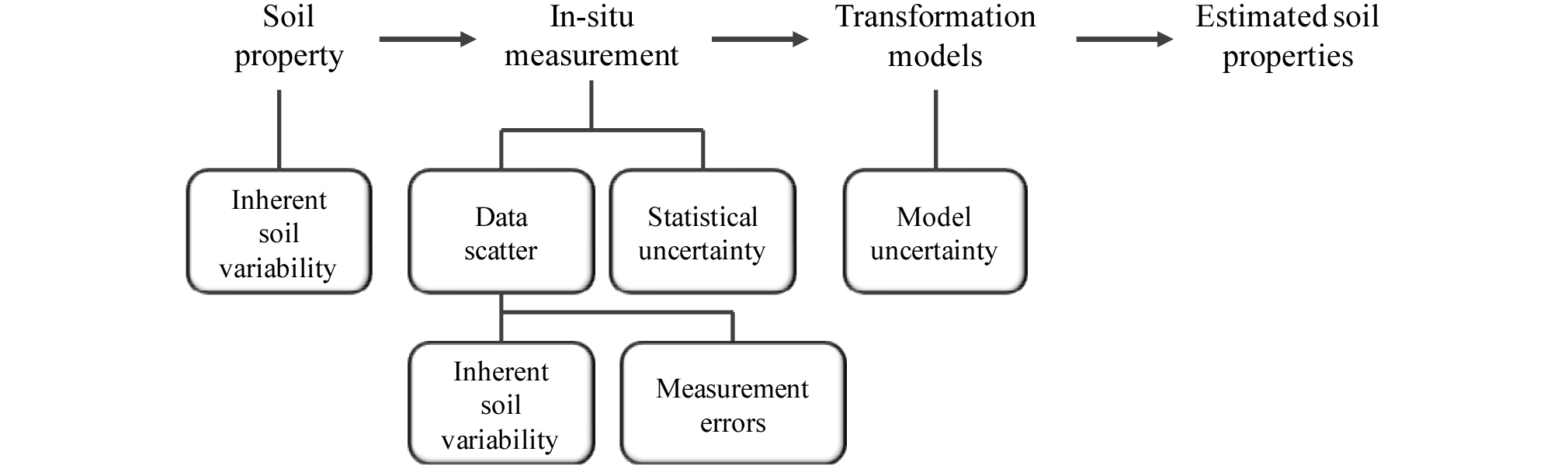
지반 공학적 문제 해석에 사용되는 대부분의 토질 역학적 정수들은 생성단계에서부터 고유한 불확실성을 갖고 있으며, 여기에 측정오차, 실험오차, 해석모델의 오차 등으로 인한 불확실성이 더해지게 된다(Christian, 2004; Lacasse and Nadim, 1996; Whitman, 2000; Ronold, 1992; De Groot and Baecher, 1993). Kulhawy(1992)은 지반 물성 예측에서의 불확실성은 고유 변동성(inherent variability), 측정오차(measurement errors)와 변환 불확실성(transformation uncertainty)의 세 가지 요인에 기인하는 것으로 분류하였다(Fig. 2).
지반의 고유 변동성은 다양한 지질학적, 환경적, 물리화학적 과정에 의해 발생하며 이들 과정들은 계속 진행되면서 지반 물성이 변하게 된다. 이러한 자연적 과정 때문에 현장 지반 물성(Y)은 수직적, 수평적인 공간에서 매우 다양하게 나타난다. 깊이(z)에 따른 공간적 변동성은 식 (9)와 같이 추세 함수, T(z)와 변동성분, v(z)로 분리할 수 있으며 변동성분은 지반의 고유한 변동성을 의미한다.
| $$Y(z)=T(z)+v(z)$$ | (9) |
일반적으로 지반의 물성은 물리적 수단에 의하여 측정되는데, 이러한 측정 과정에서 지반의 불확실성이 추가되므로 측정된 지반물성 Tm(z에는 측정오차 e(z)가 포함되어 식 (10)으로 표현할 수 있다(Lumb, 1971; Orchant et al., 1988).
| $$Y_m(z)=Y(z)+e(z)$$ | (10) |
측정오차 e(z)는 장비, 측정절차, 시험자, 임의 시험오차(random testing errors) 등에 의해 발생한다. 이러한 측정오차는 지반의 고유한 변동성분과는 서로 관련이 없는 원인으로부터 발생하므로 지반 물성과의 상관성은 없는 것으로 가정된다(Baecher, 1986; Filippas et al., 1988).
지반 공학적 실험에 의한 직접적인 측정치는 적절한 설계 변수값으로 변환하기 위한 변환모델이 필요하다. 대부분의 변환모델은 시험적 결과의 적합(fitting)을 통하여 얻어지므로 불확실성의 정도를 어느 정도 파악할 수 있다. 하지만 변환 불확실성, ε(z)은 이론을 이상화(idealization), 단순화(simplification)하는 과정에서 여전히 존재한다. 변환모델에서 데이터의 분산은 확률론적 방법을 사용하여 정량화할 수 있다. 일반적인 변환모델은 회귀분석을 통하여 평가되며 회귀곡선에서 데이터의 분산정도는 평균이 0인 확률변수(random variable)로 모델링된다. 확률변수의 표준편차는 변환 불확실성의 양을 나타낸다.
최종적으로 현장 지반물성은 지반의 고유한 변동성, 측정오차, 변환 불확실성을 포함하므로 식 (11)과 같이 표현할 수 있다. 이러한 구성요소에 대한 변동성은 2차 확률 모멘트를 이용하여 일관되게 결합할 수 있다(Phoon et al., 1995).
| $$Y(z)=T(z)+v(z)+e(z)+\varepsilon(z)$$ | (11) |
3. 결과 및 고찰
3.1 연구대상지
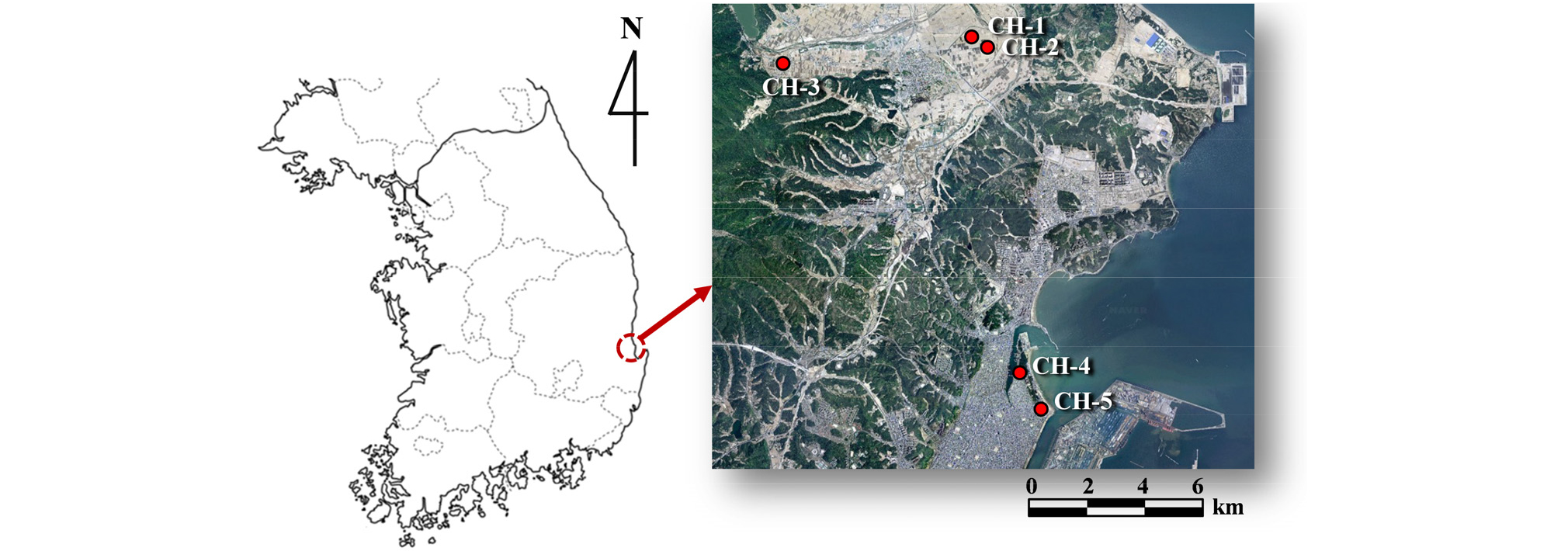
연구대상지는 경상북도 포항시로 광역적으로 경상분지에 해당한다. 대표적인 단층은 양산단층과 울산단층이 있고, 양산단층과 울산단층의 동쪽 부분에 해당하는 포항지역은 신생대 제3기층이 분포하고 있다. 2017년 규모 5.4의 지진에 따른 액상화 현상이 관측된 5개 지점(CH-1∼CH-5)에 대하여 국립재난안전연구원에서 수행한 지반조사 자료를 활용하였으며 지반조사 위치는 Fig. 3에 나타내었다.
5개의 지반조사 지점에 대하여 SPT와 CPT가 수행되었으며, 시추조사는 SPT와 병행하여 수행되었다. 이중 세립분 함량은 5개의 시추공에서 총 10개의 지점에 대하여 측정되었으며, Table 2는 시료가 채취된 지점의 지반 물성치 및 CPT결과를 정리한 것이다.
Table 2. Summary of laboratory test and CPT results
3.2 세립분 함량 예측식 적용성 분석
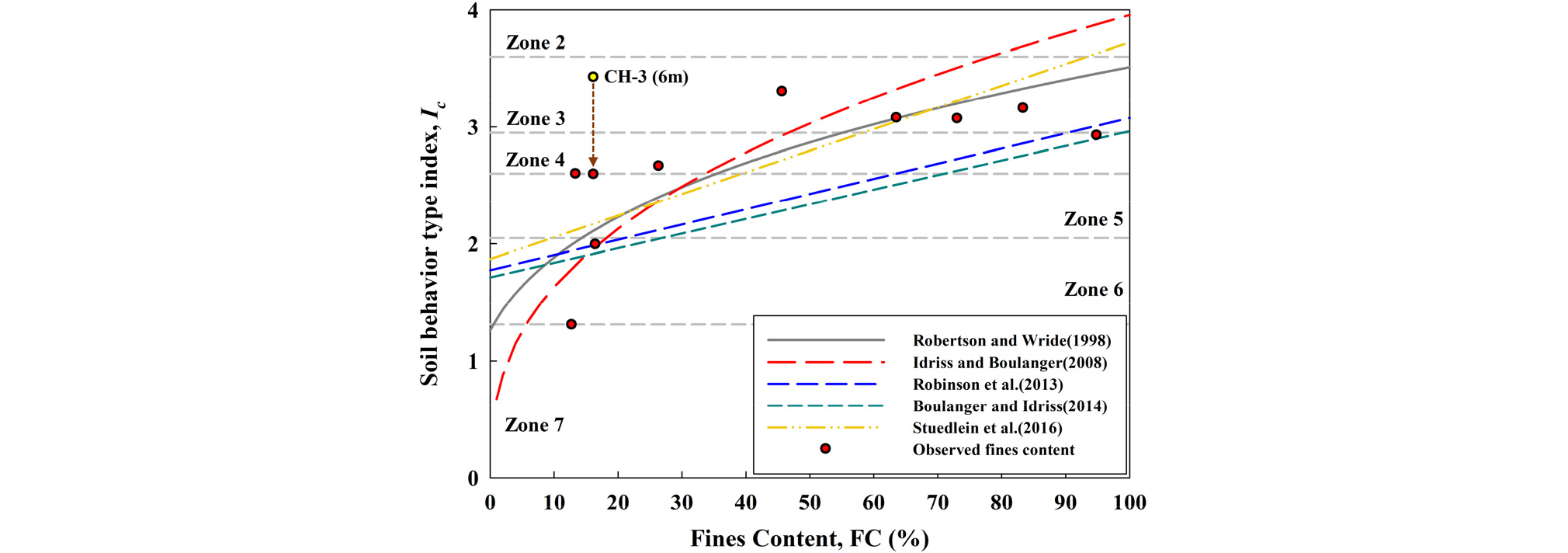
현장에 대한 세립분 함량은 5개의 시추공으로부터 총 10개의 데이터를 획득하였다. 기존의 세립분 함량 예측식의 적용성을 분석하기 위하여 각 예측식에서 산정된 세립분 함량과 실측된 세립분 함량을 비교하여 예측 오차를 평가하였다. Fig. 4는 세립분 함량 측정값과 측정위치의 CPT 결과로부터 산정된 Ic 값을 점으로 표시한 후 기존의 예측곡선과 비교하였다.
여기서 CH-3의 심도 6m에 대한 Ic는 3.42이며 세립분 함량은 16.2%로 모든 예측식과 비교하여 많은 차이가 발생함을 알 수 있다. 일반적으로 동일한 지역이라 하더라도 지표면 표고의 차이, 측정오차 등에 따라 CPT가 수행된 지점과 세립분 함량이 측정된 지점의 토층이 정확히 일치하지 않을 수 있다. 특히, 토층의 물성이 급격하게 변하는 구간의 경우 예측에 의한 오차보다 CPT와 시추공 사이의 심도 불일치에 따른 오차가 크게 발생할 수 있다. CH-3의 경우 심도 6m 부근 토층의 물성이 급격하게 변하였으며, 심도 6m에 대한 CPT에 따른 지반분류는 점토이지만 시추 주상도에 따른 지층은 소량의 자갈 및 점토가 섞인 실트질 모래로 서로 다르게 나타났다. 그러나, 심도 5.92m의 경우 CPT에 따른 Ic는 2.56로 8cm 밖에 차이가 나지 않음에도 불구하고 심도 6m의 Ic와 비교하여 매우 큰 차이를 보였으며, CPT에 의한 지반분류는 시추 주상도에 따른 지층분류와 잘 일치하는 것으로 나타났다. 그러므로, CH-3의 심도 6m에 대한 세립분 함량 예측에 대한 오차는 예측식에 따른 오차라기보다 CPT와 세립분 함량이 측정된 심도의 불일치에 따른 오차가 주원인이라 판단하여 CPT에 따른 Ic값을 심도 6.0m 대신 5.92m에 대한 값을 분석에 활용하였다. 기존 예측식들에 대한 오차평가 결과는 Table 3에 정리하였다.
Table 3. Error evaluation of prediction models for fines content prediction
b : Root mean square error
오차평가 결과, Robertson and Wride(1998)에 의한 예측식이 16.9%로 가장 작은 MAE를 갖는 것으로 나타났으며, Stuedlein et al.(2016)에 의한 예측식이 18.1%로 두 번째로 작은 MAE를 갖는 것으로 나타났다. RMSE의 경우 Robertson and Wride(1998)와 Stuedlein et al.(2016)에 의한 예측식이 21.0%로 거의 동일하며 가장 작은 오차를 갖는 것으로 나타났다. 예측식의 선정에 있어서 추가적으로 고려할 점은 예측 오차의 변동성이다. 평균 오차가 동일하더라도 예측 오차에 대한 변동성이 낮다는 것은 예측에 대한 신뢰도가 더 높다는 것을 의미한다. 비록 MAE는 Robertson and Wride(1998)가 Stuedlein et al.(2016) 보다 낮게 나타났지만 1.2%밖에 차이가 나지 않는 반면, 예측 오차에 대한 변동성은 Robertson and Wride(1998)가 Stuedlein et al.(2016) 보다 14.7% 크게 나타났다. 그러므로, 최종적으로 Stuedlein et al.(2016)에 의한 예측식이 포항지역의 세립분 함량 예측식으로 가장 적합한 것으로 판단하였다.
3.3 세립분 함량 예측 변동성 분석
가장 작은 오차를 보인 Stuedlein et al.(2016) 식의 예측 변동성을 파악하기 위하여 각 심도에서의 평균 세립분 함량 를 다음 식으로 정의할 수 있다.
| $$\overline{FC}=54t-101$$ | (12) |
여기서 t는 식 (12)에 따른 Ic의 추세를 나타내며, 2차 모멘트 확률론적 접근법에 의하여 세립분 함량의 표준편차는 Ic의 고유 변동성에 대한 표준편차(SDw), CPT데이터의 측정오차에 대한 표준편차(SDe), 그리고 식 (8)의 변환 불확실성에 따른 표준편차(SDε)을 고려하여 다음과 같이 산정할 수 있다.
| $$SD_{FC}^2=54^2(SD_w^2+SD_e^2)+SD_\varepsilon^2$$ | (13) |
이에 따라 세립분 함량의 변동성은 다음 식으로 산정할 수 있다.
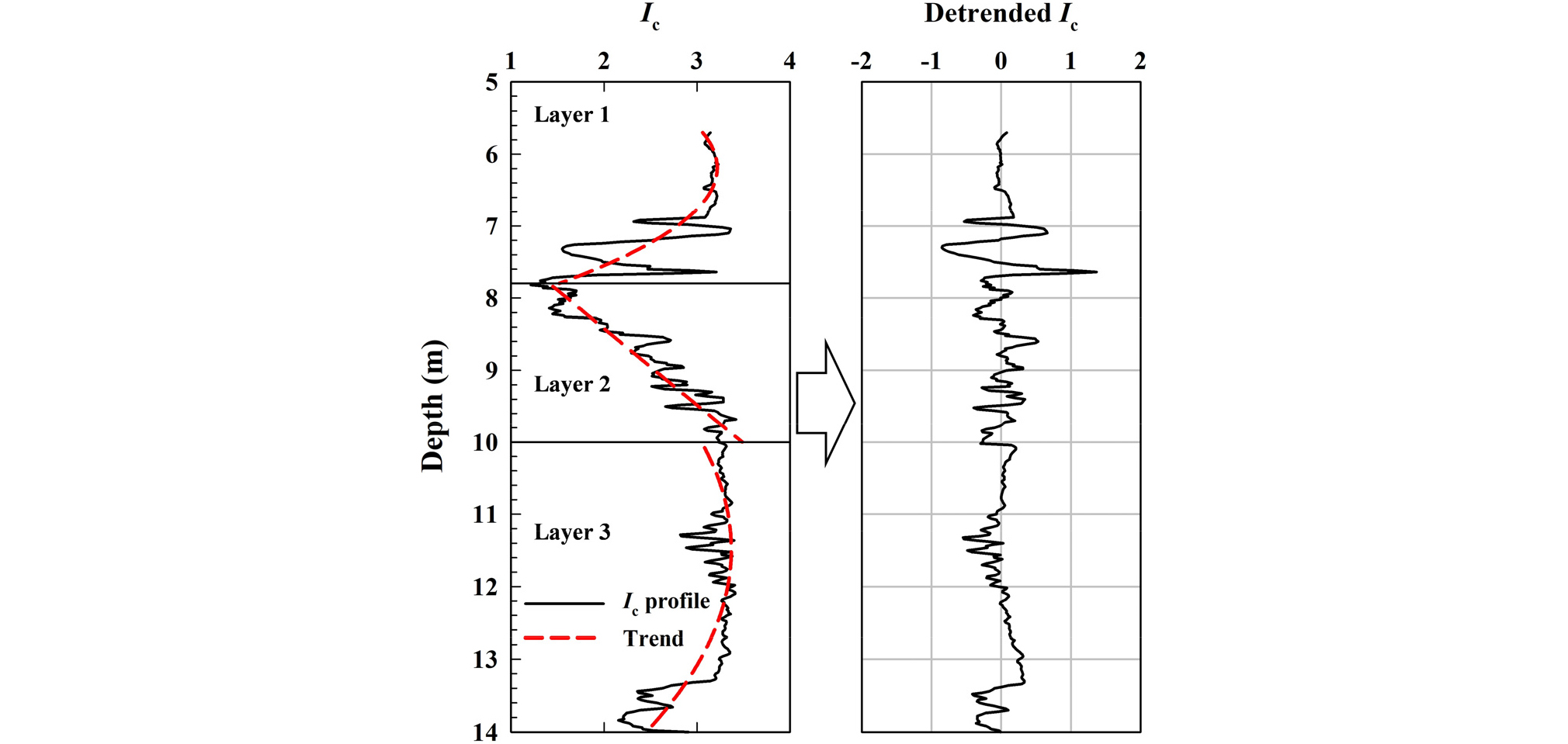
Ic에 대한 고유 변동성 (COVw)은 각 시추공에 대하여 산정하였으며 지층에 따른 분류를 고려하여 각 지층의 추세 성분을 제거한 변동성분을 분석하였다. 변동성분은 1차 또는 2차 함수를 추세 함수로 활용하여 효과적으로 분리할 수 있으며, Fig. 5는 서로 다른 지층에 대한 암석학적 변동성을 고려한 추세 성분과 변동성분의 분리에 대한 개략적인 과정을 보여준다.
5개 지점에 대한 Ic의 고유 변동성은 CPT 지점의 위치 및 지층의 종류에 따라 2.1%부터 17.8%까지 다양하게 나타났다. CPT에 따른 측정오차의 변동성(COVe)은 Kulhawy and Trautmann(1996)에 따른 문헌값을 고려하여 10%로 가정하였다. 예측식 사용에 따른 변환 불확실성에 대한 표준편차(SDε)는 10개의 실측된 세립분 함량에 대한 예측 오차로부터 산정되었으며 22.1%로 나타났다. 여기서 세립분 함량의 범위는 0∼100%이므로 세립분 함량의 표준편차에 따른 변동성 범위 또한 이 범위로 제한되어야 한다.
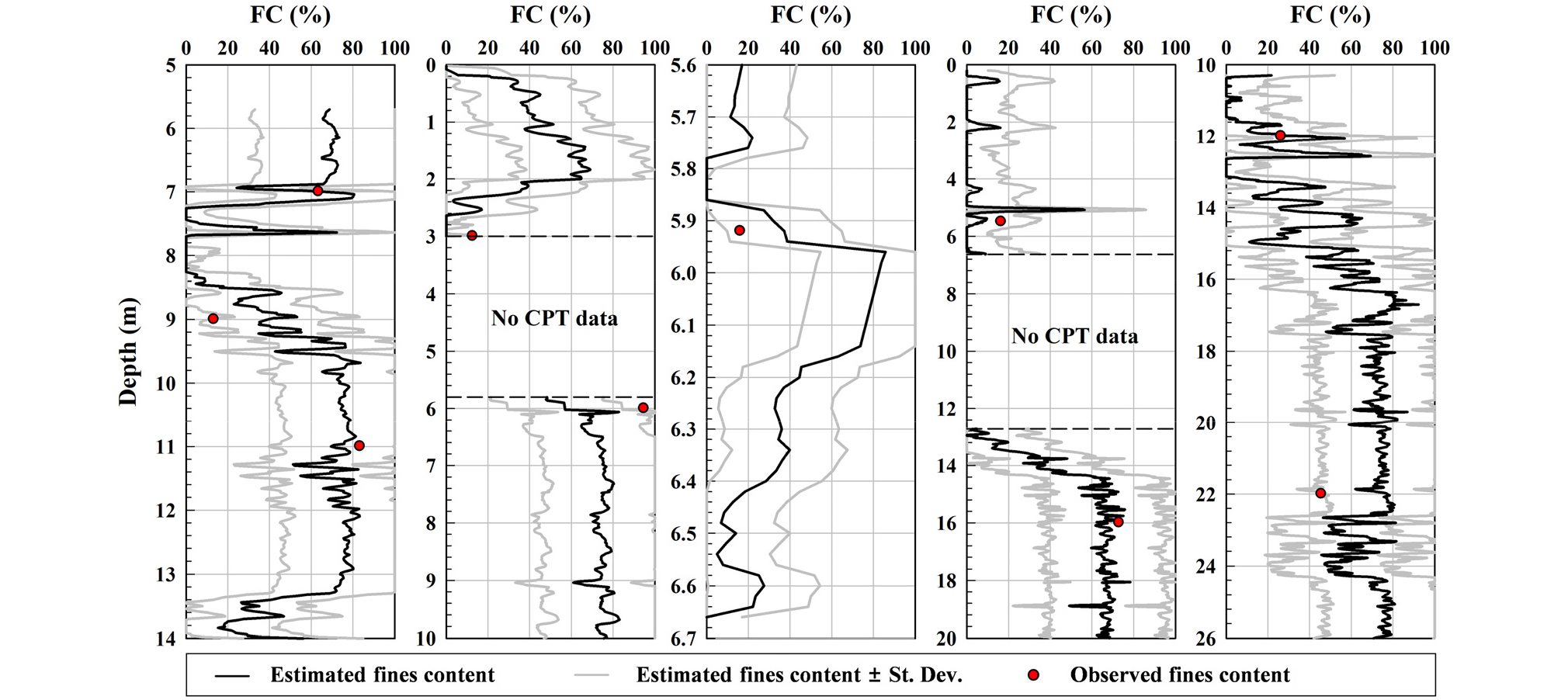
최종적으로 식 (8)에 대한 예측 변동성은 세 가지 변동성분을 모두 결합한 식 (14)를 통하여 산정할 수 있으며 5개 CPT 결과에 따른 세립분 함량 예측 및 표준편차(St. Dev.)의 ±1 분산 범위에 따른 신뢰구간은 Fig. 6과 같다.
세립분 함량 예측의 변동성에 대한 신뢰구간은 각 지점 및 지층의 고유 변동성을 고려하여 효과적으로 산정할 수 있었으며, 실측된 세립분 함량은 CPT를 통하여 예측된 세립분에 대한 표준편차의 ±1 분산 범위 안에 대부분 존재하는 것으로 나타났다. 세립분 예측에 대한 표준편차는 각 심도에 대하여 단일 값으로 산정되지만 예측값이 0∼100% 사이의 값으로 제한됨에 따라 표준편차의 ±1 분산 범위의 크기는 다르게 나타날 수 있다. 세립분 함량의 제한값을 고려한 각 지점에서 표준편차의 ±1 분산 범위에 대한 통계적 특성은 Table 4에 정리하였다.
Table 4. Statistical properties of standard deviation for fines content prediction
세립분 함량 예측에 대한 표준편차는 평균 14.9∼26.9%로 기존에 제안된 세립분 함량 예측식 중에서 포항지역 지반과 가장 적합한 모델을 선정하였음에도 불구하고 다소 높은 것으로 나타났다. 이러한 예측에 대한 불확실성은 그 원인을 제거하거나 감소시킴으로써 줄일 수 있다. 지반의 고유한 변동성은 지반의 생성단계에서부터 발생하는 불확실성으로 제거하거나 감소시킬 수 없는 불확실성으로 알려져 있다. 측정에 따른 불확실성은 CPT 장비의 정확도 개선 및 측정 중 발생할 수 있는 우연적, 인적 오차를 제거함에 따라 감소시킬 수 있지만 이를 정량적으로 평가하고 제거하기에는 한계가 있다. 또한, CPT의 측정오차는 다른 현장시험에 비하여 매우 낮은 것으로 알려져 있다. 반면, 변환 불확실성은 세립분 함량 예측 변동성의 가장 큰 원인으로 Ic와 세립분 함량 사이의 상관관계를 정확하게 파악하여 반영함에 따라 효과적으로 감소시킬 수 있다. 또한, 제안된 예측식들 중에서 가장 적합한 예측식을 선정하여 활용하더라도 대상지역에 대한 토양특성을 반영하기에는 한계가 있으므로 추후 추가적인 데이터 획득을 통하여 현장에 대한 Ic와 세립분 함량 사이의 상관관계를 도출하여 활용한다면 보다 신뢰성있는 결과를 얻을 수 있을 것으로 판단된다.
4. 요약 및 결론
본 연구에서는 CPT 기반 액상화 평가 수행 시 세립분 함량 예측에 대한 유효성을 평가하기 위하여 포항지역의 CPT 및 실측 세립분 함량 결과를 활용하여 기존 예측식들에 대한 오차를 평가하였으며, 포항지역에 가장 적합한 예측식을 선정하였다. 그리고, 지반의 고유한 불확실성을 평가하기 위하여 각 지점 및 지층에 따른 분류를 고려한 지반의 변동성분을 분석하였으며 CPT의 측정오차, 예측식 사용에 따른 변환 불확실성을 함께 고려하여 CPT를 통한 세립분 함량 예측에 따른 변동성을 평가하였다. 본 연구의 결과를 요약하면 다음과 같다.
(1) CPT를 활용한 세립분 함량에 대한 기존 예측식은 Ic와 세립분 함량의 상관관계가 도출된 지반의 종류 및 회귀식의 형태에 따라 예측 범위가 매우 다양하게 나타났으며, 동일한 CPT 결과라 하더라도 세립분 함량의 예측값은 약 50%까지 차이가 발생할 수 있다.
(2) 2017년 포항지진에서 액상화 현상이 관측된 5개 지점에 대한 CPT 및 10개의 실측 세립분 함량을 통한 기존 예측식들의 오차평가 결과, Stuedlein et al.(2016)에 의한 세립분 함량 예측식이 18.1%의 MAE와 이에 대한 변동성이 62.3%로 포항지역의 세립분을 예측하기에 가장 적합한 것으로 나타났다.
(3) 세립분 함량 예측에 대한 변동성을 평가하기 위하여 각 지점에서 Ic의 추세성분을 제거한 변동성분을 분리하고 이에 대한 고유 변동성을 평가하였으며, CPT의 위치 및 지층의 종류에 따라 2.1∼17.8% 변동성이 나타났다. CPT의 측정오차는 10%로 가정하였으며, 변환 불확실성은 Stuedlein et al.(2016)의 예측식에 대한 오차평가로부터 22.1%의 표준편차를 갖는 것으로 나타났다.
(4) 2차 모멘트에 대한 확률론적 접근법을 통하여 Ic의 고유 변동성, 측정오차, 변환 불확실성을 고려한 세립분 함량의 예측 변동성을 산정하였으며, 표준편차의 ±1 분산 범위에 따른 신뢰구간을 산정하였다. 실측된 세립분 함량은 예측된 세립분 함량에 대한 표준편차의 ±1 분산 범위 안에 대부분 존재하는 것으로 나타났다. 이러한 예측 변동성의 정량적 분석결과는 향후 액상화 평가에 대한 신뢰성 해석에서 세립분 함량에 대한 불확실성을 반영하는 기초자료로 활용될 수 있다.
(5) Stuedlein et al.(2016)에 의한 예측식은 기존 예측식들 중 가장 적합한 것으로 나타났지만 여전히 예측 변동성은 높게 나타나므로 예측값의 신뢰범위를 고려하여 적용할 필요가 있다. 또한, 예측 변동성의 주요인은 변환 불확실성에 의한 것으로 추후 포항지역의 CPT를 통한 Ic와 세립분 함량의 상관관계를 통하여 예측식을 도출하고 활용한다면 세립분 함량 예측의 변동성을 감소시킬 수 있을 것으로 판단된다.