1. 서 론
2. 최적화 방법
2.1 모의강화법(Simulated Annealing Method)
2.2 차분진화 알고리즘(Differential Evolution Algorithm)
2.3 입자 군집 최적화 알고리즘(Particle Swarm Optimization Algorithm)
3. 차분진화 알고리즘의 지반공학 분야 적용성 분석에 사용된 이론 공식
3.1 Sharan의 이론 해
3.2 Blum’s method(흙막이벽체 근입깊이 산정 방법)
4. 다변수 적용 모델 최적화 방법 비교
4.1 수치적 유효성 검토(numerical validation)
4.2 결과 분석
5. 결 론
1. 서 론
지반은 본질적으로 비균질(heterogeneous), 비등방(anisotropic) 그리고 불확실성(uncertainty)을 내포하고 있기 때문에, 지반 내부를 굴착하는 터널 및 흙막이벽체 시공을 진행 전까지는 불확실한 부분이 많아서 설계단계에서 모든 현상을 완벽하게 예측하기는 불가능하다. 터널 및 흙막이벽체 시공 중 계측값은 설계단계에서의 예측값과 일치하는 경우가 드물고, 이러한 두 값이 크게 달라지는 경우도 빈번하게 발생한다. 예측값과 계측값의 차이가 터널 및 흙막이벽체 시공의 안정관리에 미치는 영향을 신속하게 판단하여야 할 필요성이 있다. 시공 중 터널 및 흙막이벽체의 안정성을 계측값에 의해서 평가하고, 그 결과를 다음 시공단계 예측에 활용할 수 있는 방법으로 역해석이 있다. 역해석은 다양한 매개변수와 수치적 표현이 가능한 문제에 대해서 수행된다. 역해석의 주요한 가정에는 분석 결과와 예측한 값이 일치되도록 변경하는 과정이 포함된다. 이러한 과정은 Peck(1969)에 의해서 지반공학적인 개념으로 제시되었다. 더 나아가, 현재 운영 중인 터널, 사면, 댐 등 다양한 토목구조물에 대한 역해석을 통해 신뢰성 있는 안정성 평가가 가능할 것으로 판단된다.
Kim and Jang(1995)은 계측자료를 활용하여 지반변형계수와 정지토압계수에 대한 터널 역해석 방법을 제안하였다. Yang and Jeon(2002)은 지반변형계수와 정지토압계수를 유한차분해석 프로그램인 FLAC2D에 내장되어있는 FISH언어를 사용한 역해석 방법을 제안하였고, 직접탐색법 중에 하나인 단변량법(univariate method)을 사용하였다. Kim and Lee(2013)는 유한차분법과 직접탐색법 중에 하나인 로젠브록법(rosenbrock method)을 조합한 터널역해석 방법을 제안하였다. 상기 기술한 연구는 2변수 수준의 지반공학 역해석에 관한 연구이며, 역해석 방법 중 결정론적인 방법이 적용되었다. 이후 연구자들은 지반공학 다변수 문제 해결을 위해서 확률론적인 방법을 적용하기 시작하였다. Vardakos et al.(2012)은 차분진화 알고리즘(Storn and Price, 1997)과 유전자 알고리즘(Simpson and Priest, 1993)을 사용하여 터널 주변 지반의 물성을 계산하기 위한 역해석 방법을 제안하였다. 이 연구에서는 FLAC2D 프로그램을 사용하였고, 다양한 역해석 알고리즘을 구축하여 적용성을 검증하였다. 이후, 국내에서도 많은 연구자들에 의해서 차분진화 알고리즘의 지반공학적 접근이 시도되었다(Kim, 2017; An, 2017). An and Song(2018)은 운영 중 해저터널의 안정성을 분석하기 위하여 변위와 응력 계측데이터를 적용하였다. 운영 중 터널에서는 보강지반의 열화(degradation), 콘크리트 라이닝의 열화 및 온도변화 등 다양한 요인으로 구조물의 안정성의 변화가 발생할 수 있기 때문에 운영 중 구조물의 안정성 평가를 위해서는 다변수(multivariate) 역해석이 필요하다. 또한, 기하조건, 경계조건 및 재료물성을 이용한 이론적 변위값과 계측된 변위값이 상이할 경우 운영중인 지반구조물에 대한 신뢰성 있는 안정성 분석을 위해서는 다변수 역해석의 도입이 요구된다.
상기 기술한 터널문제에 대하여 차분진화 알고리즘의 적용성을 확인하였고, 지반공학 문제에 대한 다변수 역해석 기술의 적용성을 파악하기 위해서 본 연구를 진행하였다. 본 연구에서는 역해석 수행 시에 해석공간이 복잡하고, 설계변수가 많은 상황을 해결할 수 있는 최적화 방법을 도출하기 위해서 몇 가지 최적화 방법에 대하여 비교하였다. 결정론적 방법 중에서는 모의강화법(simulated annealing method, SA), 확률론적 방법 중에서는 차분진화 알고리즘(differential evolution algorithm, DEA), 입자 군집 최적화 알고리즘(particle swarm optimization algorithm, PSO)을 선택하고, 지반공학 분야에 대한 이론식에 대해서 단순한 다변수 모델을 적용해서 최적화 방법을 비교하였다.
2. 최적화 방법
지반공학 관련 물성의 추정문제는 필연적으로 비선형 함수 문제를 포함하고 있다. 그러므로 지반공학 분야의 역해석 수행 시 비선형 최적화 알고리즘이 많이 사용되고 있다. 최적화 방법 중에 일반적으로 직접법(direct method)이 많이 사용되며, 직접법은 결정론적 방법과 확률론적인 방법으로 구분된다. 전자의 종류에는 모의강화법(simulated annealing method), 로젠브록법(rosenbrock method), 단변량법(univariate method), 황금분할법(golden section search method) 등이 있으며, 후자의 종류에는 진화 알고리즘(EA), 차분진화 알고리즘(DEA), 입자 군집 최적화 알고리즘(PSO), 유전자 알고리즘(GA) 등이 있다. 여기서는 본 연구에서 사용된 모의강화법, 차분진화 알고리즘, 입자 군집 최적화 알고리즘에 대해서 요약해서 기술하였다.
2.1 모의강화법(Simulated Annealing Method)
Kirkpatrick et al.(1983)에 의해서 최초 제안된 모의 강화법(simulated annealing method, SA)은 국부해(local minimum)에 수렴되는 단점을 개선한 최적화 방법 중에 하나이다. 기본 원리가 단순하고, 다양한 분야에 사용할 수 있는 SA는 전역해(global minimum)에 대한 수렴성이 이론적으로 증명되어서 많은 분야에 적용되고 있지만, 적용 상 미해결 문제점들을 내포하고 있다. 특히, 계산 시간이 오래 걸리는 단점이 있다(Saab and Rao, 1991). 목적함수의 값을 상승이동(uphill movement) 시키는 확률은 메트로폴리스 기준(metropolis criterion)이라고 불리는 식 (1)로 계산된다.
| $$P(E)\;\;\infty\;\;\exp\left(\frac{-E}{kT}\right)$$ | (1) |
여기서, 식 (1)은 열역학적 공식이며, 시스템이 각 온도 T에서 평형상태가 된다면, 에너지는 다양한 에너지 레벨(E)에 확률적으로 분포됨을 표현한다. 현재의 해 근처에 새로운 해를 만들거나 확률적으로 새로운 해를 발생시켜 비교하여 국부해를 탈출할 수 있으며, 이 과정을 반복하여 최적해를 찾을 수 있다.
2.2 차분진화 알고리즘(Differential Evolution Algorithm)
Storn and Price(1997)에 의하여 제안된 차분진화 알고리즘은 비선형, 미분 불가능한 연속공간함수를 빠르게 탐색하여 최적해(optimal minimum)를 구하기 위한 목적으로 제안되었다. 이 방법은 유전자 알고리즘과 기본적인 연산과정이 유사하며, 초기 개체군을 랜덤하게 생성하고, 돌연변이(Mutation), 교배(Crossover), 선택(Selection) 등의 단계를 거쳐 다음 세대를 구성한다. 이전 세대의 개체 집단 에서 무작위로 선택된 임의의 3개 개체들로부터 교배용 벡터를 식 (2)와 같이 생성한다. 여기서, NP는 집단의 크기이고, F는 돌연변이 상수로 0∼2 사이의 값을 갖는다.
| $$v_{i,G+1}=X_{r1,G}+F\cdot(x_{r2,G}-x_{r3,G})$$ | (2) |
| $$x_{i,G+1}=\left\{\begin{array}{l}u_{i,G+1}\;\;\mathrm{if}\;\;f(u_{i,G+1})\;\leq\;\;f(x_{i,G}),\\x_{i,G}\;\;\;\;\;\;\;otherwise\end{array}\right.$$ | (4) |
식 (3)은 교배단계를 설명하고, 시행벡터(trial vector)를 생성하기 위해 부모개체와 돌연변이벡터(mutant vector)가 교배된다. 여기서 rand는 변화에 사용될 벡터가 무작위로 선택됨을 의미하며, CR은 교배상수로 0에서 1 사이의 값을 갖는다. 는 [1, 2, ..., D]의 무작위 정수(integer)이다. 한 연속공간함수를 빠르게 탐색하여 최적해(optimal minimum)를 구하기 위한 목적으로 제안되었다. 식 (4)는 선택 단계에 대한 내용이다. 목표벡터(target vector) 를 시행 벡터 와 비교하고, 교배상수에 의해 다음 세대를 구성할 개체를 선택한다. 지정된 세대수가 도달하거나, 새로운 개체가 최적값을 만족할 때까지 진화 연산은 반복 수행된다.
2.3 입자 군집 최적화 알고리즘(Particle Swarm Optimization Algorithm)
PSO(Particle Swarm Optimization)는 Eberhart and Kennedy(1995)에 의해서 제안되었다. PSO는 최적화 문제를 풀기 위해서 생물체의 사회적 행동 양식을 모방하고 있다. PSO에서는 개별 잠재해를 입자(particle)로 나타낸다. 즉, 결정변수의 개수가 m이라면 PSO에서의 탐색공간은 m차원의 실수 공간이 되고, t시점에서의 j번째 입자 는 의 실수벡터로 나타난다. t시간의 j번째 입자의 속도는 식 (5)에 의해 결정된다.
| $$v_j(t+1)=w(t)\cdot v_j(t)+c_1\cdot r_1\cdot(pbest_j(t)-x_j(t))+c_2\cdot r_2\cdot(gbest(t)-x_j(t))$$ | (5) |
| $$x_j(t)=v_j(t)+x_j(t-1)$$ | (6) |
여기서, w(t)는 이전속도에 대한 관성하중, c1, c2는 가속상수, r1, r2는 (0, 1)의 난수, pbest는 개별 입자의 반복 이동을 통해서 발견된 최적해, gbest는 모든 입자의 반복 이동을 통해서 발견된 최적해이다. 관성하중 값과 속도 값이 계산되면 입자는 식 (6)을 사용하여 현재 위치에서 다음 세대의 위치로 이동한다. 이와 같은 방법을 통해 입자들은 탐색 공간을 이동하며, 적합도 함수에 의한 평가 결과에 따라 보다 적합한 위치로 이동한다. 입자 군집 최적화 알고리즘은 최적해를 찾기 위하여 이 과정을 반복 수행한다.
3. 차분진화 알고리즘의 지반공학 분야 적용성 분석에 사용된 이론 공식
3장에서는 역해석 및 최적화 방법 적용을 위한 지반공학 분야의 대표적인 이론 공식을 선정하였다. Sharan(2003)의 터널 굴착면에서 변위 예측 식, Blum(1931)의 흙막이벽체 길이 산정 방법에 대해서 기술하였고, 후술하는 4장에서 이 2가지 공식에 대해서 SA, DEA, PSO 방법에 대한 지반공학 분야의 적용성을 분석하였다.
3.1 Sharan의 이론 해
Sharan(2003)은 정수압 응력조건 하에 있는 취성파괴 암반에 대한 터널 굴착면에서의 변위예측 이론 해를 제안하였다. Sharan이 제안한 지중 원형 굴착면에 대한 변위 예측 식에 대해서 결정론적 방법과 확률론적 방법으로 최적화에 대한 비교 분석을 수행하였다. Fig. 1(a)에서는 Sharan이 제안한 변위 예측 식을 유도한 가정된 굴착면과 주변 지반 및 응력 조건을 보여주고 있다. 또한, Fig. 1(b)에서는 elastic-brittle-plastic 거동 모델에 대한 응력-변위 곡선을 보여주고 있다.
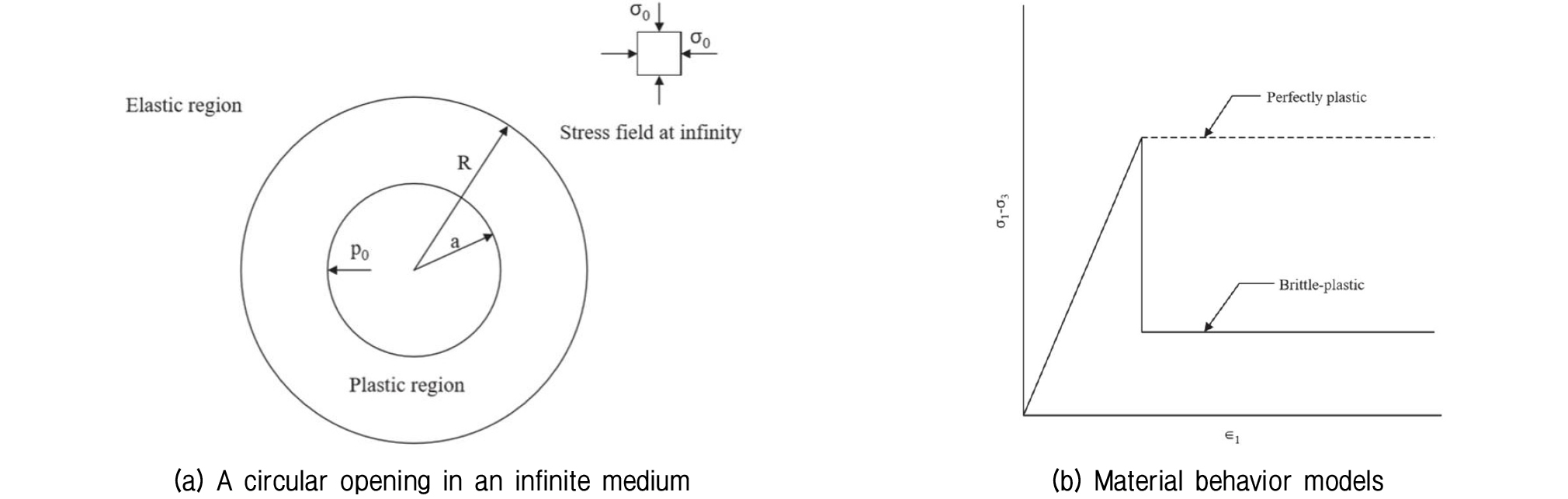
Fig. 1.
Prediction of theoretical displacement solution on tunnel excavation surface for rock mass (Sharan, 2003)
Sharan(2003)이 제안한 elastic-brittle-plastic 거동 모델에 대한 지중 원형 굴착면에서 발생 내공변위에 대한 이론 해는 r = a일 때, 식 (7)과 같다.
| $$u_0=\frac{(1+\nu)}Ea^{-K_d}\left[C(1-2\nu)\left(R^{K_d+1}-a^{K_d+1}\right)-D\left(R^{K_d-1}-a^{K_d-1}\right)\right]+u_R\left(\frac Ra\right)^{K_d}$$ | (7) |
여기서, , , , , ,
r : 굴착 반경(m)
σc : Intact rock의 일축압축강도(MPa)
mr, sr : Hoek-Brown 상수(Brittle-plastic 상태)
m, s : Hoek-Brown 상수(Plastic 상태)
E : 굴착면 주변 암반의 변형계수(GPa)
ν : 굴착면 주변 암반의 포아송비
ψ: 팽창각
σ0 : 원지반 초기응력(MPa)
p0 : 굴착면에서 암반 방향으로 작용하는 내압(MPa)
3.2 Blum’s method(흙막이벽체 근입깊이 산정 방법)
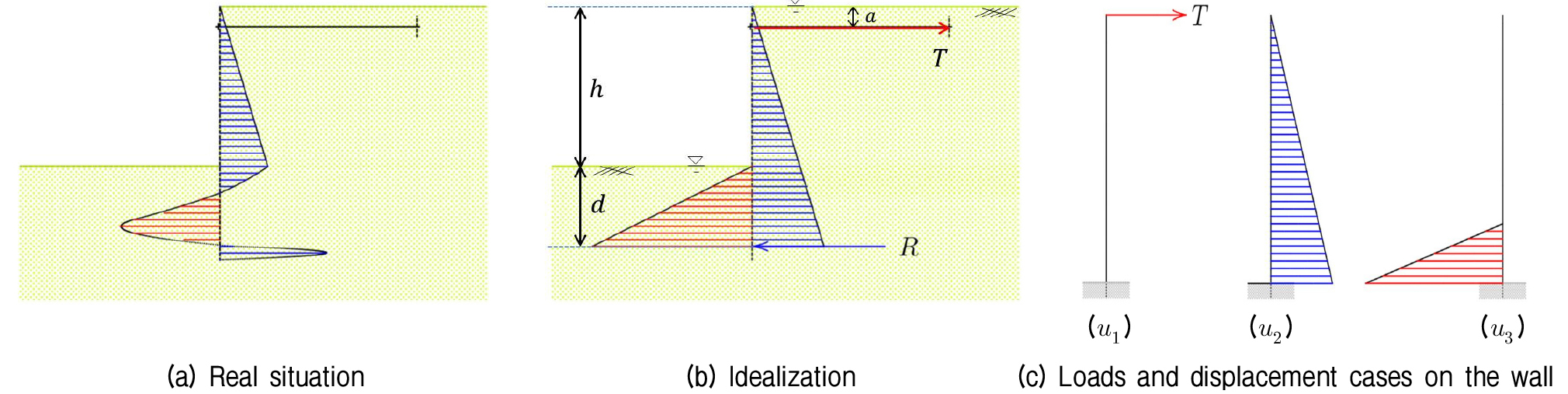
널말뚝벽체의 길이가 평형상태를 유지하기 위해서 필요한 길이보다 조금이라도 크다면, 수동토압을 벽체의 전 길이에 걸쳐 고려할 필요는 없다. 벽체에 가해지는 압력은 Fig. 2(a)와 같은 형태가 될 것으로 예상된다. Blum(1931)은 Fig. 2(b)와 같이 벽체에 작용되는 하중을 도식화하도록 제안했다. R은 벽체 최하단부 오른쪽에서 작용하는 힘으로 가정하고, 정확한 크기는 결정하지 않은 상태로 둔다. Blum의 schematization에서 흙막이벽체 선단부는 클램프된 모서리(clamped edge)로서, 휨모멘트는 0이지만, 전단력(R)이 허용된다고 가정하였다.
Blum 방법의 기본 원리는 널말뚝벽체의 선단부에서 완전히 clamping되는 것으로 간주되며, 선단부에서의 휨모멘트가 0으로 고려되지만, 전단력은 일반적으로 0이 아니므로, 전단력은 선단부 부근에 작용되는 합력으로 가정된다. 이 방법의 수행절차는 Fig. 2(b)로 설명할 수 있다. 여기서, 포화된 지층에 근입된 벽체 길이를 h와 d로 구분하고, 지하수위는 지표면과 일치시킨다. 또한 지표면으로부터 1st 앵커까지의 깊이는 a, 앵커력은 T로 정의한다. 여기서 h값은 기지값이며, 근입깊이 d는 미지값으로서, 해석에 의해서 결정되는 매개변수 중 하나이다.
| $$u_1=\frac{T(h+d-a)^3}{3EI}$$ | (8) |
| $$u_2=\frac{K_a^\ast\gamma(h+d)^5}{30EI}$$ | (9) |
| $$u_3=\frac{K_p^\ast\gamma d^5}{30EI}+\frac{K_p^\ast\gamma d^4h}{24EI}$$ | (10) |
여기서, γ: 흙의 단위중량, γw: 물의 단위중량
h : 굴착깊이, d : 근입깊이, T : 앵커력
E : 벽체의 탄성계수, I : 벽체의 단면 2차모멘트
a : 지표면에서 1st 앵커까지 깊이
Ka* : 정수압을 고려한 주동토압계수 (=Ka(1-γw/γ)+(γw/γ)), Ka : 주동토압계수
Kp* : 정수압을 고려한 수동토압계수 (=Kp(1-γw/γ)+(γw/γ)), Kp : 수동토압계수
식 (11)은 벽체에 설치된 앵커에 의해서 힘 T가 작용하는 경우에 대해서, 빔(beam) 부재에 대한 고전적인 휨 이론에 근거한 벽체 변위(u1), 주동토압에 의한 벽체 변위(u2) 및 수동토압에 의한 벽체 변위(u3)의 총합은 0임을 사용해서 전개한 h와 d의 관계식이다.
| $$\left(\frac dh\right)^3=\frac{8\left(K_a^\ast/K_p^\ast\right)\left(1+d/h\right)^5}{20\left(1+d/h\right)^2-15d/h-12\left(d/h\right)^2}$$ | (11) |
4. 다변수 적용 모델 최적화 방법 비교
4장에서는 전술한 바와 같이, PSO, SA, DEA 방법을 사용해서 Sharan(2003)의 이론 해, Blum(1931)의 공식에 대한 다변수 설계 조건의 최적화 계산을 수행하여 지반공학 분야에 대한 적용성을 검토하였다.
4.1 수치적 유효성 검토(numerical validation)
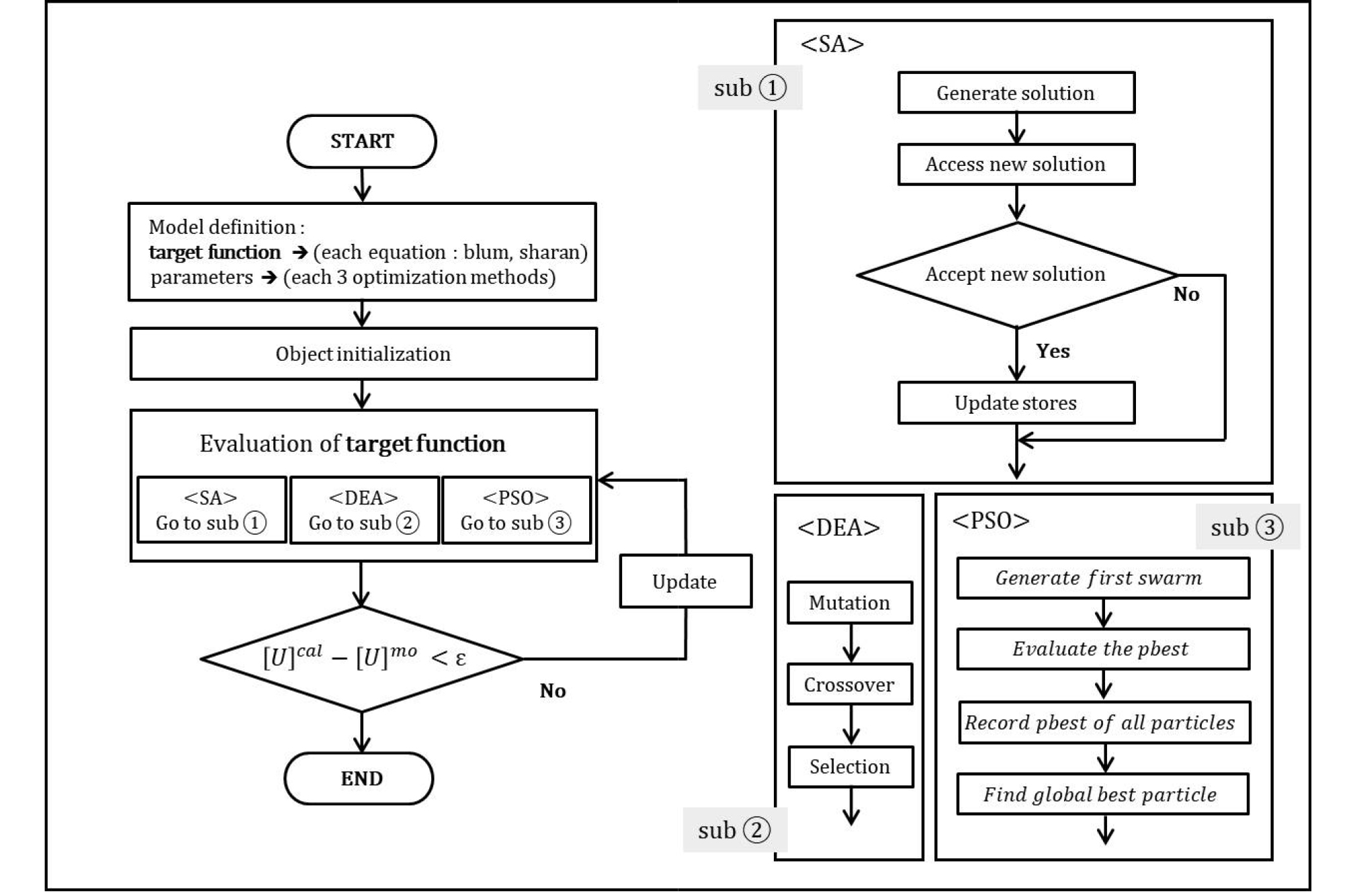
본 연구에서 사용한 2가지 공식 및 3가지 알고리즘에 대해서 Fig. 3과 같이 결합하여 구성하였으며, python 언어로 코딩하여 목표 변수 및 초기값의 범위를 조절하며 비교 및 분석을 수행하였다. Fig. 3에서는 수행 방법에 대한 순서도를 보여주고 있다. 입력 물성치 및 목표변수의 탐색 범위는 다양한 연구에 사용된 내용(Hoek et al., 2000; Hong et al., 2004; Sharan, 2005; Sim et al., 2015)을 참고하여 결정하였으며, Table 1, 2에서 보여주고 있다. 다변수 최적화 계산을 위해서 각 공식에 대해서 5가지의 목표변수를 선택했고, 2변수∼5변수 범위에서 계산을 수행하였다. 목표변수는 Sharan의 이론 해에 대해서, mr, m, E, σ0, p0이며, Blum의 방법에서 γ, , E, d, a이다. 값은 주동 및 수동토압계수 계산에서 사용되었다. 지반정수, 벽체의 강성 및 길이, 하중 등을 선택하여 목표변수로 설정하였다.
Table 1. Input parameter and range of targets for Sharan’s equation
Table 2. Input parameter and range of targets for Blum’s equation
4.2 결과 분석
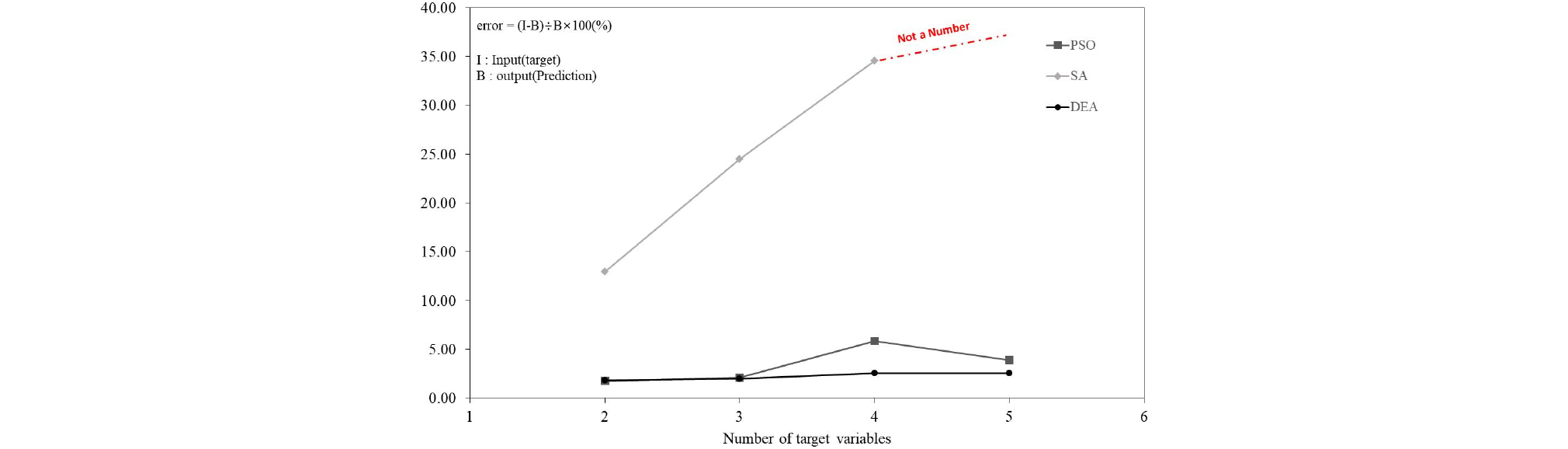
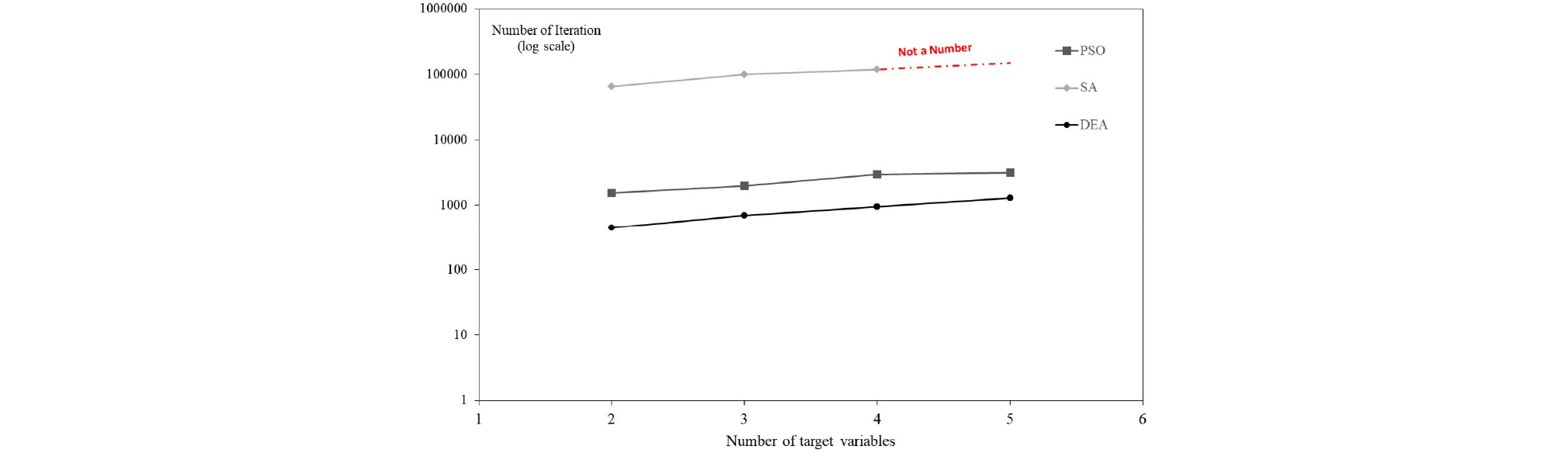
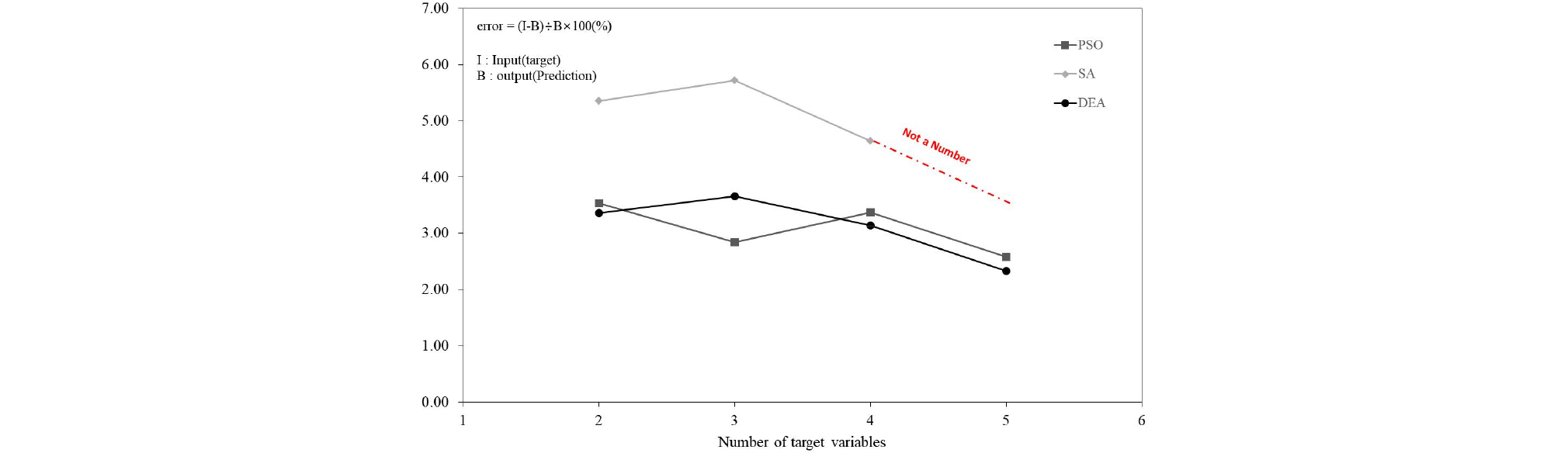
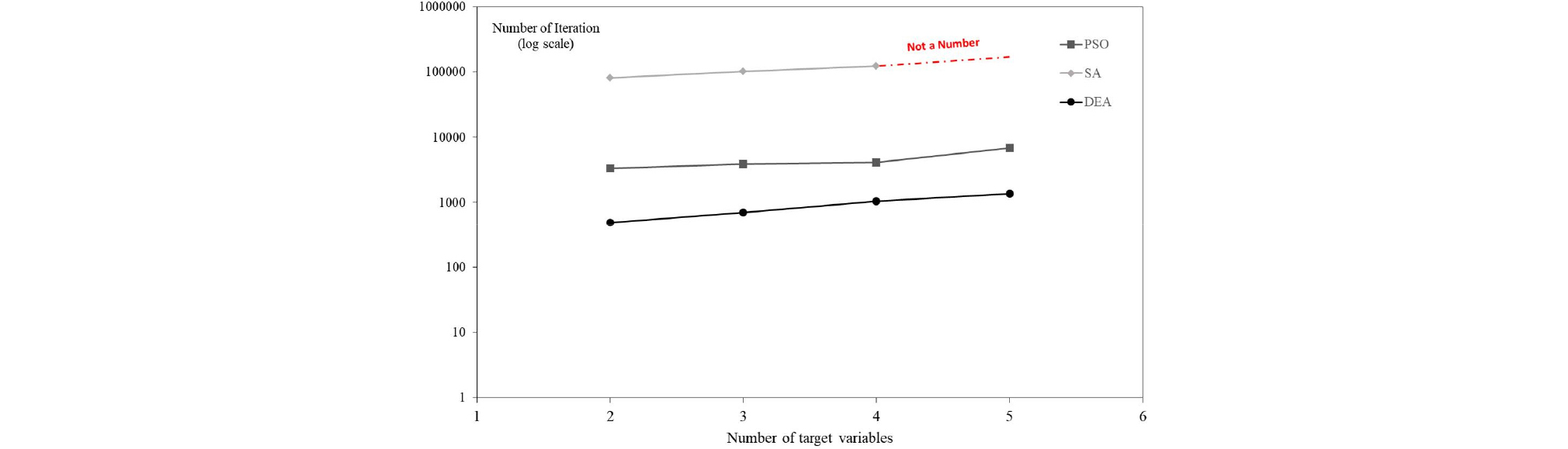
Fig. 4∼7에서는 Sharan의 이론 해 및 Blum의 방법에 대해서 PSO, SA, DEA 방법에 대한 성능을 비교한 결과를 보여주고 있다. 목표변수 개수 대비 역해석 오차율 및 반복계산 회수에 대해서 각각 도시하였다. 또한, Table 3∼5에서는 모든 수치해석에 대한 결과를 보여주고 있다.
Table 3. Results of the error rates for PSO, SA and DEA (Sharan’s equation)
Table 4. Results of the error rates for PSO, SA and DEA (Blum’s equation)
Table 5. Results of the number of iteration for PSO, SA and DEA
결정론적인 방법인 SA는 최적해(global minimum) 탐색시간이 상대적으로 오래 걸리는 것으로 확인되었고, 또한, 5변수 문제에서는 두 가지 공식에 대해서 모두 해를 찾지 못하는 결과를 보였다. 확률론적인 방법인 PSO 및 DEA는 지반공학 관련 다변수 문제에 적용성이 있는 것으로 결과가 산정되었다. 특히, DEA는 Sharan 및 Blum 문제에 대해서 5변수 문제에서도 3% 수준의 오차율을 보였고, 탐색시간도 가장 빠른 것으로 파악되었다. DEA 대비해서 SA는 117.39∼167.13배, PSO는 2.43∼6.91배의 반복 탐색 회수가 소요되었다. 이러한 결과를 토대로 차분진화 알고리즘(DEA)이 지반공학 문제에 대한 다변수 역해석 문제에 적용성이 우수한 것으로 판단되었다. 3가지 최적화 방법에 대한 비교를 통해서 차분진화 알고리즘(DEA)이 터널굴착면 및 흙막이 벽체 문제에 대하여 적용성이 우수한 것으로 분석되었다. 향후 지속적인 연구를 통해 다양한 지반공학 문제에 적용하여 DEA의 신뢰성과 수렴속도를 향상 시킬 수 있다면, 보다 실시간에 가까운 역해석 및 이를 통한 운영 중 사회인프라 구조물의 안정성 평가가 가능할 것으로 사료된다.
5. 결 론
지반공학 분야에 대한 차분진화 알고리즘(DEA)의 다변수 역해석 분야의 적용성 분석을 위해서, Sharan의 이론 해 및 Blum의 방법에 대해서 수치해석을 수행한 결론은 아래와 같다.
(1) 3가지 최적화 방법에 대해서 지반공학 분야 다변수 역해석을 수행한 결과, 결정론적인 방법인 SA는 다른 방법들에 비해서 상대적으로, 최적해 탐색 시간이 오래 걸렸고, 오차율이 너무 컸으며, 5변수 문제에서는 해를 찾지 못하는 결과를 보였다. 지반공학 역해석 문제에서 SA 방법은 다른 방법에 비해서 상대적으로 적용성이 떨어지는 것으로 판단된다.
(2) 확률론적인 방법인 PSO 및 DEA는 지반공학 관련 다변수 문제에 적용성이 있는 것으로 결과가 산정되었다. 특히, DEA는 Sharan의 이론 해에 대한 문제에서 평균 3.12%, Blum 문제에 대해서 평균 2.23%의 오차율을 보였고, 반복 탐색 회수도 가장 작은 것으로 파악되었다. DEA 대비해서 SA는 117.39∼167.13배, PSO는 2.43∼6.91배의 반복 회수가 소요되었다.
(3) 3가지 최적화 방법에 대한 비교를 통해서 차분진화 알고리즘(DEA)이 터널굴착면 및 흙막이 벽체 문제에 대하여 적용성이 우수한 것으로 분석되었다. 향후 지속적인 연구를 통해 다양한 지반공학 문제에 적용하여 DEA의 신뢰성과 수렴속도를 향상 시킬 수 있다면, 보다 실시간에 가까운 역해석 및 이를 통한 운영 중 사회인프라 구조물의 안정성 평가가 가능할 것으로 사료된다.