1. 서 론

2017년 11월 15일 포항지진으로 인한 액상화 사례가 국내 처음으로 보고된 이 후로 국내 액상화 취약 지반 보강 공법에 대한 관심이 높아지고 있다. 이에 따라 액상화 취약 지반 보강에 효과적인 공법 중 하나인 압밀 그라우팅(compaction grouting)에 대한 관심도 높아지고 있다. 압밀 그라우팅은 Graf(1969)에 의해 처음 제시된 공법으로 유동성이 매우 낮은 저유동성 그라우트(low mobility grout, LMG)를 지반에 주입하여 그라우트 구근을 형성하고 그 팽창 압력으로 지반을 다짐으로써 연약지반을 보강하는 공법이다. 기타 그라우팅 공법들이 지반의 고결화를 목적으로 하는 반면(Nam et al., 2018), 압밀 그라우팅은 그라우트 구근의 팽창 압력으로 지반을 보강하는 공법이기 때문에 대상 지반을 균일하게 보강할 수 있으며 상대적으로 경제적이라는 장점이 있다. 또한 시공 시 과잉 간극수압이 발생하지 않는 한 지하수위에 크게 영향을 받지 않는다. 이러한 장점들로 인해 압밀 그라우팅 공법은 액상화 취약 지반 보강에 효과적이라고 알려져 있다.

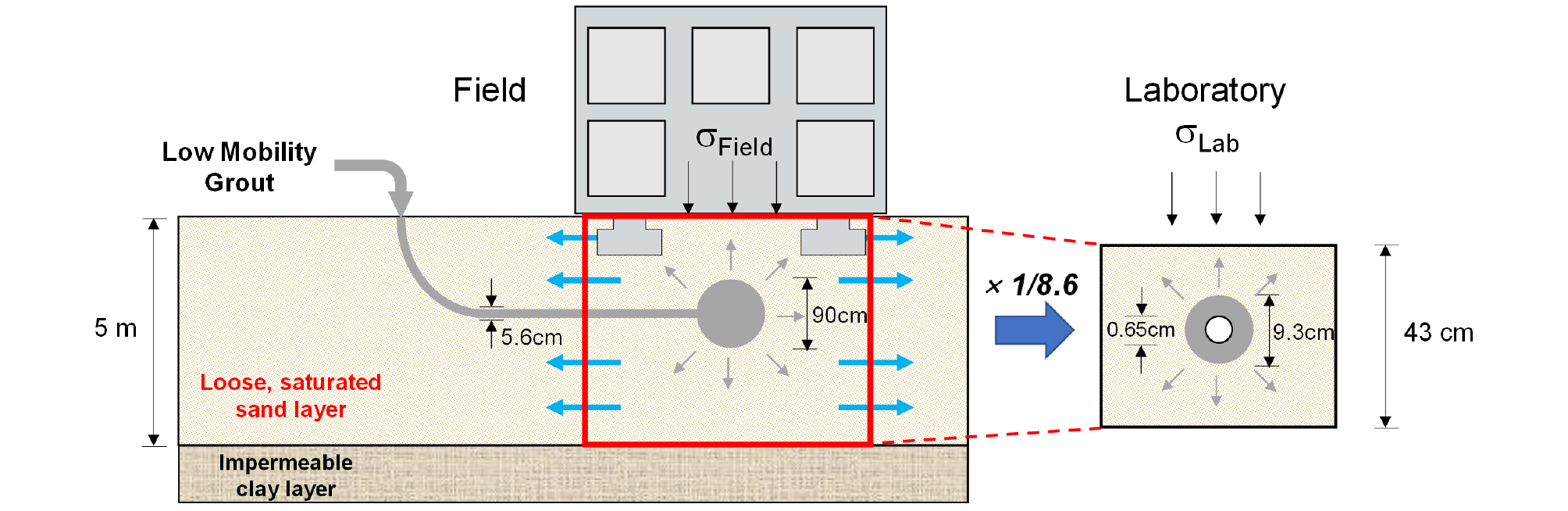
압밀 그라우팅 공법은 대상 지반의 물성, 그라우트 주입 간격 및 주입 압력, 주입공의 직경 등 복합적인 인자에 영향을 받으며 Wong(1971, 1974)에서 제시된 모델을 이용하여 주로 수직 주입 압밀 그라우팅 설계를 진행한다. 최근에는 수치해석, 실내실험, 현장실험을 통해 압밀 그라우팅 공법의 주요 영향 인자, 시공 효율, 표면 융기 조건 등에 대한 연구가 활발히 진행되고 있다(Nichols and Goodings, 2000; Wang et al., 2009; El-Kelesh et al., 2001; 2012; Wang et al., 2015). 하지만 아직도 압밀 그라우팅 공법 설계는 선행 시공 결과에 따른 경험적인 모델에 많이 의존하고 있는 실정이다(El-Kelesh et al., 2001). 이론적인 모델과 현장의 시공 결과간 차이의 원인 중 하나는 그라우트 구근 형상의 단순화에 있다. 대부분의 선행 연구들은 그라우트 구근 형상을 구형으로 가정하여 연구를 진행하였다. 하지만 실제 지반에서는 지반의 응력 이방성에 의해 그라우트 구근이 완벽한 구형으로 형성되지 않으며 이로 인해 이론적인 예측과 실제 시공 결과의 차이가 발생한다. 또 대상 지반에 기존 상부 구조물이 있는 경우 그라우트 수직 주입이 어려워 수평방향으로 그라우트를 주입하여야 한다(Fig. 1). 하지만 수평 압밀 그라우팅에 대한 연구는 또한 국내·외적으로 매우 드문 실정이다.

Fig. 1

A benchmark model of horizontal compaction grouting

따라서 본 연구에서는 느슨한 사질토에서의 수평 압밀 그라우트의 구근 형상 발달을 규명하고자 하였다. 상사비를 고려한 2차원 축소 모형에서 액상화 취약 지반을 모사한 후 압밀 그라우트를 수평으로 주입하는 실험을 다양한 상재하중 조건에서 수행하였다. 압밀 그라우트의 주입 중 시간에 따른 그라우트 구근 형상의 발달 모습과 상재하중 및 상대밀도에 따른 최종 그라우트 구근 형상을 분석하였다.

2. 수평 압밀 그라우팅 축소 모형 실험

2.1 실험 시료

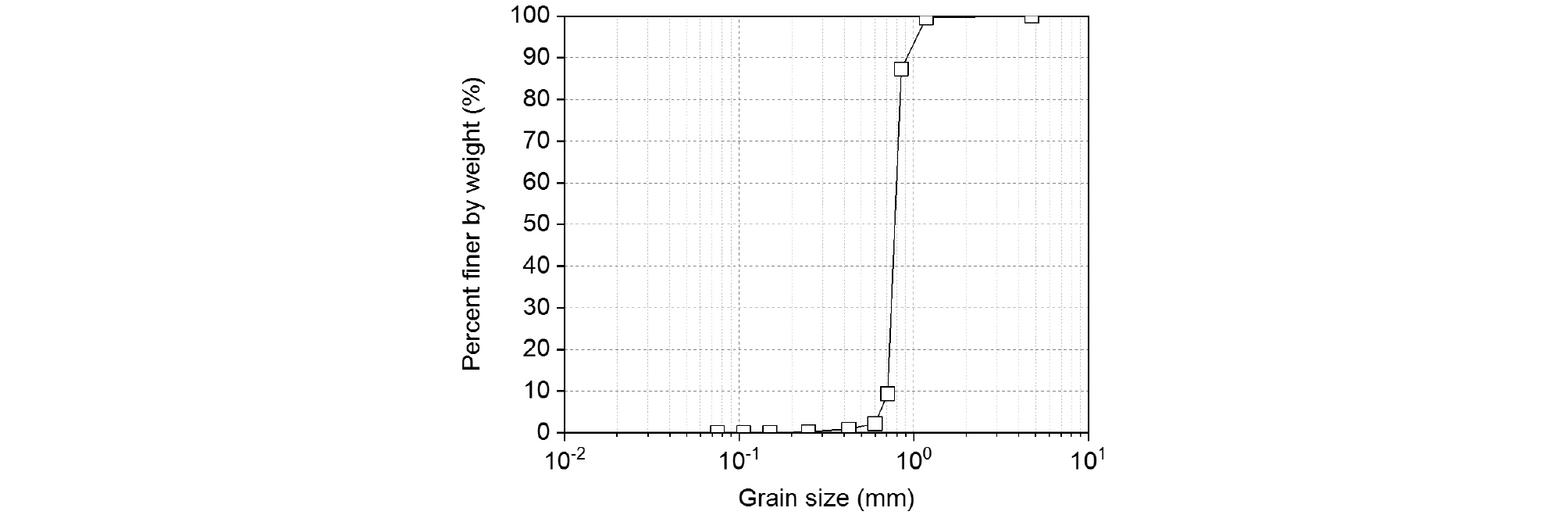
액상화 취약 사질토를 모사하기 위해 입도 분포가 불량한 조립 사질토(poorly graded sand, Ottawa 20/30, U.S. Silica, Frederick, MD, USA)를 사용하였고, 평균 입경은 770μm이다(Fig. 2). 압밀 그라우팅에 사용되는 저유동성 그라우트(low mobility grout, LMG)는 그라우트의 내부 마찰과 투수계수 유지를 위한 골재, 그라우트의 유동성을 높이기 위한 점토, 그라우트의 강도 증진을 위한 시멘트, 재료의 균일한 혼합을 위한 물을 혼합하여 만들어진다(Kirsch and Bell, 2012). 저유동성 그라우트는 지반 내 공극으로 침투하는 것을 방지하기 위해 200cP 이상의 높은 점성이 요구되며 slump test를 통해 그라우트의 적합성을 판단한다. 본 연구에서는 silica sand, bentonite clay, Portland cement, 0.045% methylene blue 수용액을 혼합하여 LMG를 만들었으며 slump 값은 5.3cm로 측정되었다. 이는 일반적으로 압밀 그라우팅에 사용되는 LMG의 슬럼프 값인 5cm과 유사하다(Nichols and Goodings, 2000). 점토의 경우 그라우트의 유동성을 높여 그라우트 주입 압력을 감소시키기 위해 사용하며 일반적으로 건조 중량 기준 골재의 1%이내로 사용한다. 하지만 실내 그라우팅 실험의 경우 원활한 그라우트의 주입을 위해 더 많은 양의 점토가 혼합되기도 하며(Nichols and Goodings, 2000) 본 연구에서는 골재의 13.3% 질량비로 점토를 혼합하여 사용하였다(Table 1).

Fig. 2

Particle size distribution of Ottawa 20/30 sand

2.2 상사비(Scaling Law)를 고려한 축소 모형 설계

현장 적용 가능한 축소 모형 실험 설계를 위해 Pater et al.(1994)에서 제시된 scaling 모델을 이용하였다. 이 모델은 지반의 탄성 변형 시 이에 따른 탄성에너지와 유체 흐름 시 마찰에 의한 에너지 손실의 비가 실제 현장과 실험실에서 동일하게 유지될 때 실험실의 환경이 현장을 대변할 수 있다는 가정에서 출발하며, 간략화 한 Pater모델식은 다음과 같다.

여기서 S는 각각 현장과 축소 모형 실험에서의 값의 비이며, 아래 첨자 E는 탄성률, d_w는 주입구의 반경, Q는 주입 유량, μ는 주입 유체 점성이다. 이 모델을 토대로 본 실험에서 그라우트의 현장 주입을 모사할 수 있는 주입 유량을 결정하는 과정은 다음과 같다.

a. 그라우트 주입구의 반경을 이용한 시료의 크기 결정

현장에서 주로 사용하는 그라우트 주입관의 반경은 56mm 정도이며, 축소 모형 실험에서 그라우트 주입관의 반경은 6.5mm로 결정하였다. 따라서 축소 모형 실험 토조 내 사질토 시료 높이가 43cm일 때 5m의 사질토층을 모사함을 알 수 있다.

b. 현장과 축소모형실험에서의 탄성률 결정

실제 현장과 축소모형실험에서 액상화 취약 사질토층의 포화 밀도는 같다고 가정한 후(1,920kg/m³) 유효응력 계산하고 다음의 경험식을 이용한 전단파 속도 계산할 수 있다.

여기서 β는 구형 입자의 경우 일반적으로 사용하는 0.25의 값을 사용하였다(Cascante and Santamarina, 1996; Santamarina et al., 2001). 이때 전단파 속도와 포아송비(υ) 0.3을 이용하여 탄성률(영탄성계수)를 결정하였다.

이를 통해 계산된 탄성률비(S_E)는 다음과 같다.

c. Pater 모델을 이용한 그라우트 주입 유량 결정

본 축소 모형 실험에서는 실제 현장과 동일한 그라우트를 사용하였기 때문에 그라우트의 점성비(S_μ)는 1이다. 위의 과정을 통해 축소 모형 내 사질토 시료의 높이를 43cm, 그라우트 주입 유량을 13~70mL/min으로 결정하였다.

2.3 실험 장치 및 방법

사용된 축소 모형 실험 토조는 40cm × 43cm × 1cm 규모이며 Fig. 3과 같다. 본 실험 장치는 그라우트의 수평주입을 모사할 수 있으며 용수철을 이용해 상부 응력을 조절하여 현장의 상부 구조물에 의한 응력 상태를 조절할 수 있다. 불투수층 사이의 사질토 지반을 모사하기 위해 사질토를 수중 낙사(wet packing) 한 후 수평방향 배수만 허용하였으며 상부 로딩 프레임을 이용하여 0, 4, 8, 16kPa의 상재 수직 응력 조건을 구현하였다. 이는 현장 상부 수직응력 0, 50, 100, 200kPa을 모사한다. 하중 재하 후 포화 사질토 시료의 상대밀도는 50~80%로 측정되었고, Meyerhof(1957)에서 제시된 변환식을 이용하여 SPT-N치로 치환 시, N치 20 미만으로 액상화에 취약한 포화 사질토 조건임을 확인 후 실험을 수행하였다.

Fig. 3

(a) A schematic diagram, (b) schematic diagram of front view of saturated sand plate, and (c) a digital photograph of the 2D test setup

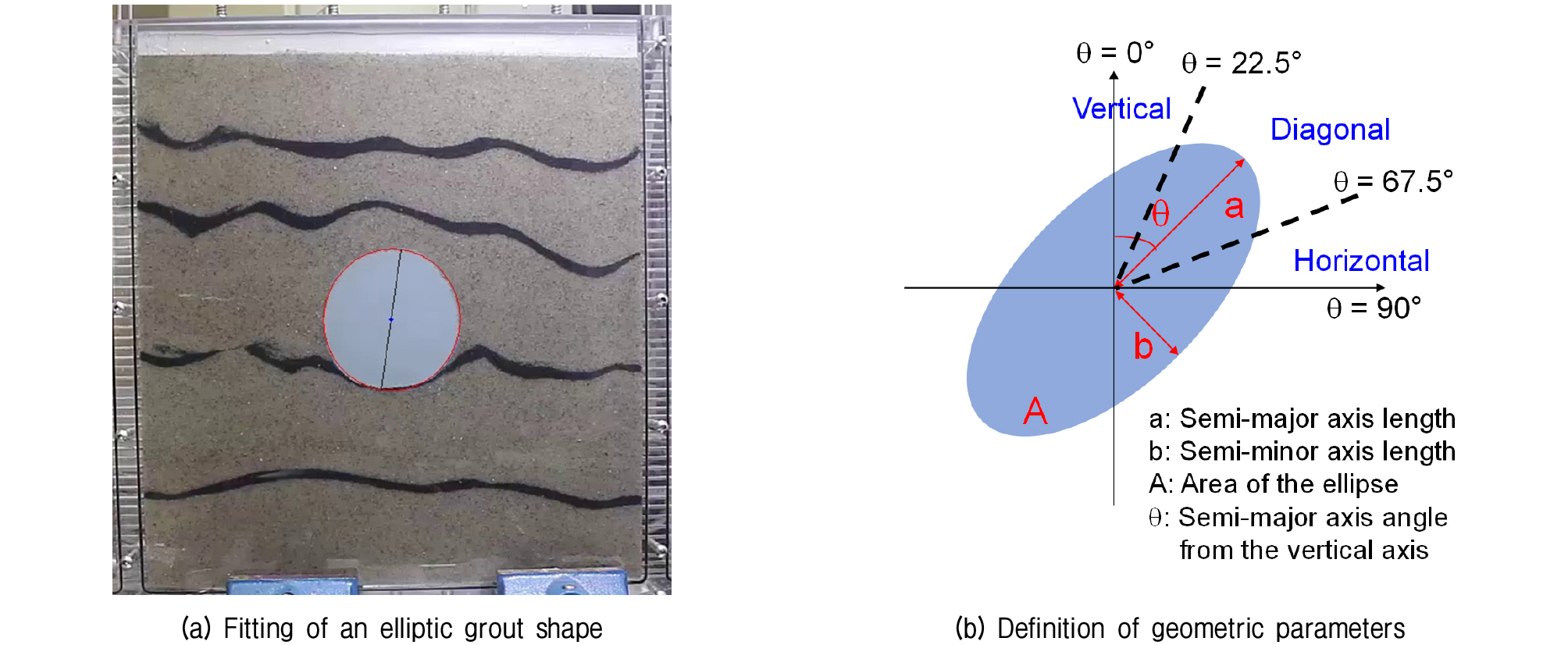
그 후 주입 펌프와 저유동그라우트를 담고 있는 transfer vessel을 이용하여 13~70mL/min의 유량으로 그라우트를 주입하였다. 동시에 그라우트 주입 과정을 촬영하여 그라우트 구근과 보강 대상 지반으로 분리하였으며 그라우트 구근을 타원 곡선 접합(curve fittining)을 통해 장축 반경(semi-major axis length; a) 단축 반경(semi-minor axis length; b), 수직축으로부터 장축의 각도(θ), 주입된 그라우트 구근의 면적(A)을 측정하였다(Fig. 4).

Fig. 4

Definition of grout shape parameters: (a) fitting of an elliptic grout shape and (b) definition of geometric parameters. The grout in (a) shows the test result of σ16Q29

3. 실험 결과 및 분석

Fig. 5는 시간에 따른 그라우트 구근 이미지 분석 결과의 예시이다. 그라우트 주입 영상의 각 프레임마다 이미지 추출을 통해 그라우트 구근의 이미지를 추출 후 이를 분석하여 시간에 따른 그라우트 구근의 면적을 측정하고 1cm의 두께를 가정하여 주입된 그라우트의 부피를 계산하였다. 또 타원 곡선 접합을 통해 장축 반경, 단축 반경, 수직축으로부터 장축의 각도를 측정하고 앞에서 측정한 구근의 단면적과 접합한 타원의 면적을 비교하여 그 오차를 계산하였다. 이를 통해 본 연구에서는 그라우트 구근의 형상을 장축과 단축 반경의 비(a/b ratio)와 그라우트 구근의 팽창 방향(θ)을 중심으로 분석하였다. a/b ratio의 경우 그라우트 구근이 원형에 근접한 정도를 나타내며 완벽한 원형의 구근이 생성되었을 때 최솟값 1을 가진다. 그라우트 구근의 팽창에 따라 그라우트 구근의 장축이 바뀌는 경우 이는 θ값의 변화로 나타난다.

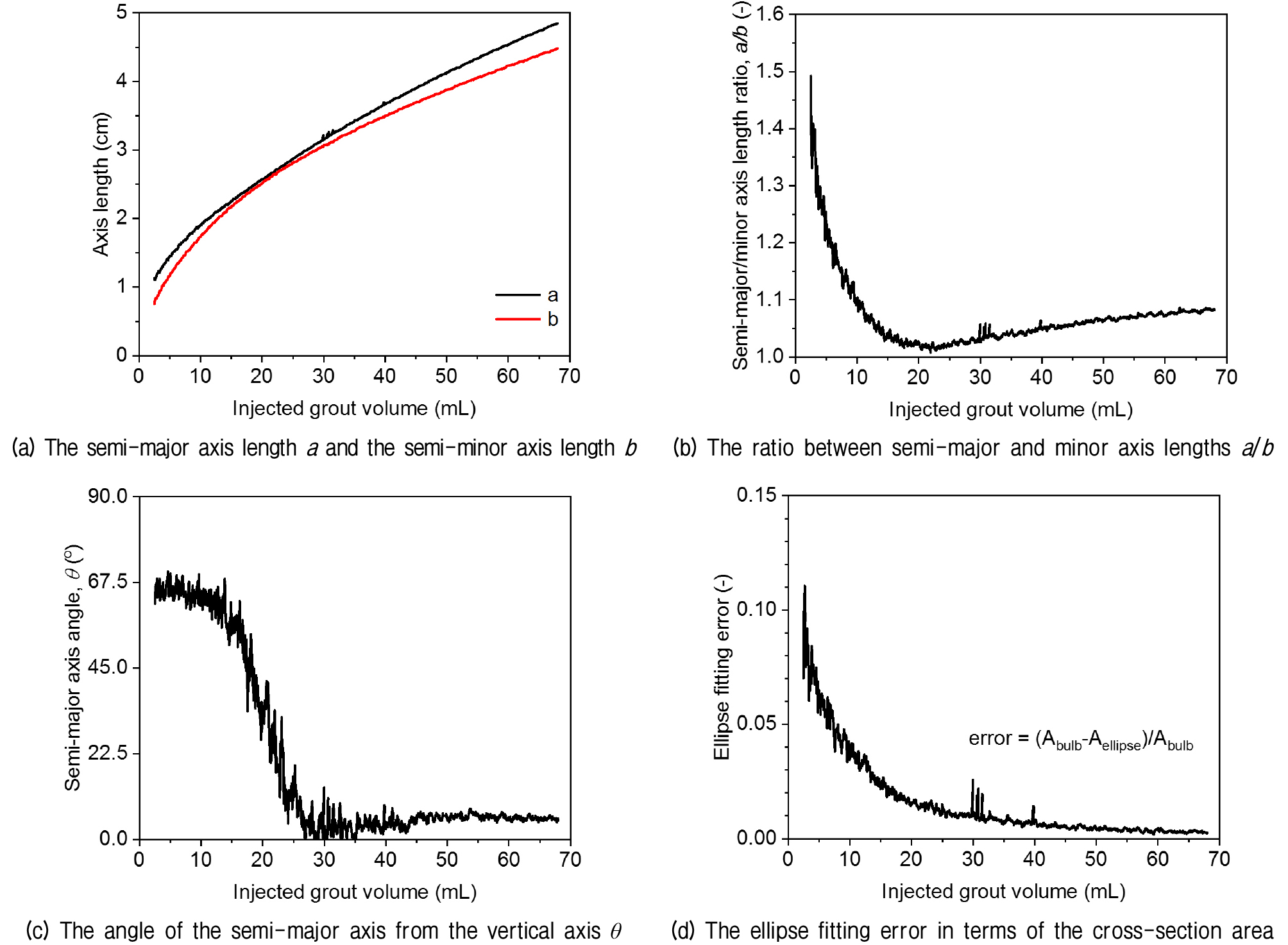
Fig. 5

An example of geometric analysis result for the test of σ16Q27: (a) the semi-major axis length a and the semi-minor axis length b, (b) the ratio between semi-major and minor axis lengths a/b, (c) the angle of the semi-major axis from the vertical axis θ, and (d) the ellipse fitting error in terms of the cross-section area

그라우트 구근 이미지 분석은 80cm직경의 현장 그라우트 구근 크기를 기준으로 축소 모형 시험에서 주입된 그라우트 면적이 68cm²이 될 시점을 기준으로 분석하였으며 68cm²에서 a/b ratio와 θ값이 수렴하지 않는 경우에 수렴한 후의 값을 기준으로 분석하였다(Table 2와 Fig. 6 참조).

Fig. 6

Images of the grout bulb. These images were captured at the point when the grout area was 68 cm². The title indicates the vertical stress condition and the flow rate. Test σ04Q14 represents the test with the vertical stress of 4 kPa and the flow rate 14 mL/min

3.1 그라우트 구근 형상: 장축과 단축의 길이비 a/b

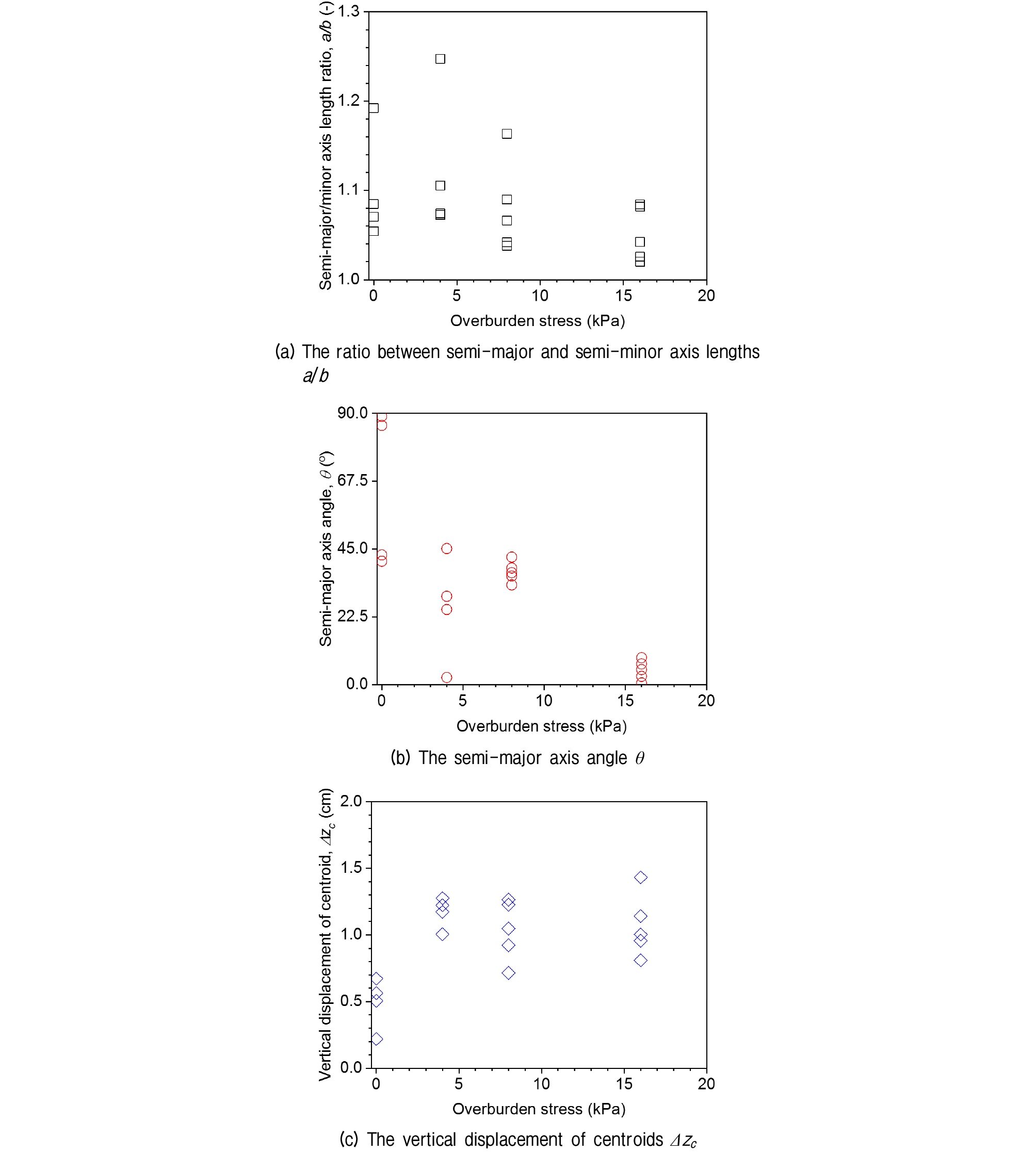
상부 응력에 따른 그라우트 구근 형상의 변화는 Fig. 7(a)와 같다. 실험 결과 상부하중이 증가함에 따라 a/b 값이 감소하며 1에 가까워지는 것을 확인하였다. 0, 4kPa로 상부 응력이 낮은 경우 a/b 값은 각각 평균 1.10과 1.13, 최대 1.19와 1.25로 그라우트 구근이 원형에서 매우 벗어난 타원의 형태로 생성되었다. 8kPa의 경우 a/b 값이 평균 1.08, 최대 1.16으로 조금 감소하였으며 16kPa의 경우 a/b 값은 각각 평균 1.05, 최대 1.08로 그라우트 구근의 형상이 상부 응력이 증가함에 따라 수평과 수직방향 사이의 이방성이 감소하여 원형에 가깝게 형성되는 것을 확인하였다.

Fig. 7

Effects of vertical effective stress on (a) the ratio between semi-major and semi-minor axis lengths a/b, (b) the semi-major axis angle θ, and (c) the vertical displacement of centroids Δz_c

3.2 그라우트 구근 팽창 방향: 수직축으로부터의 장축의 각도 θ

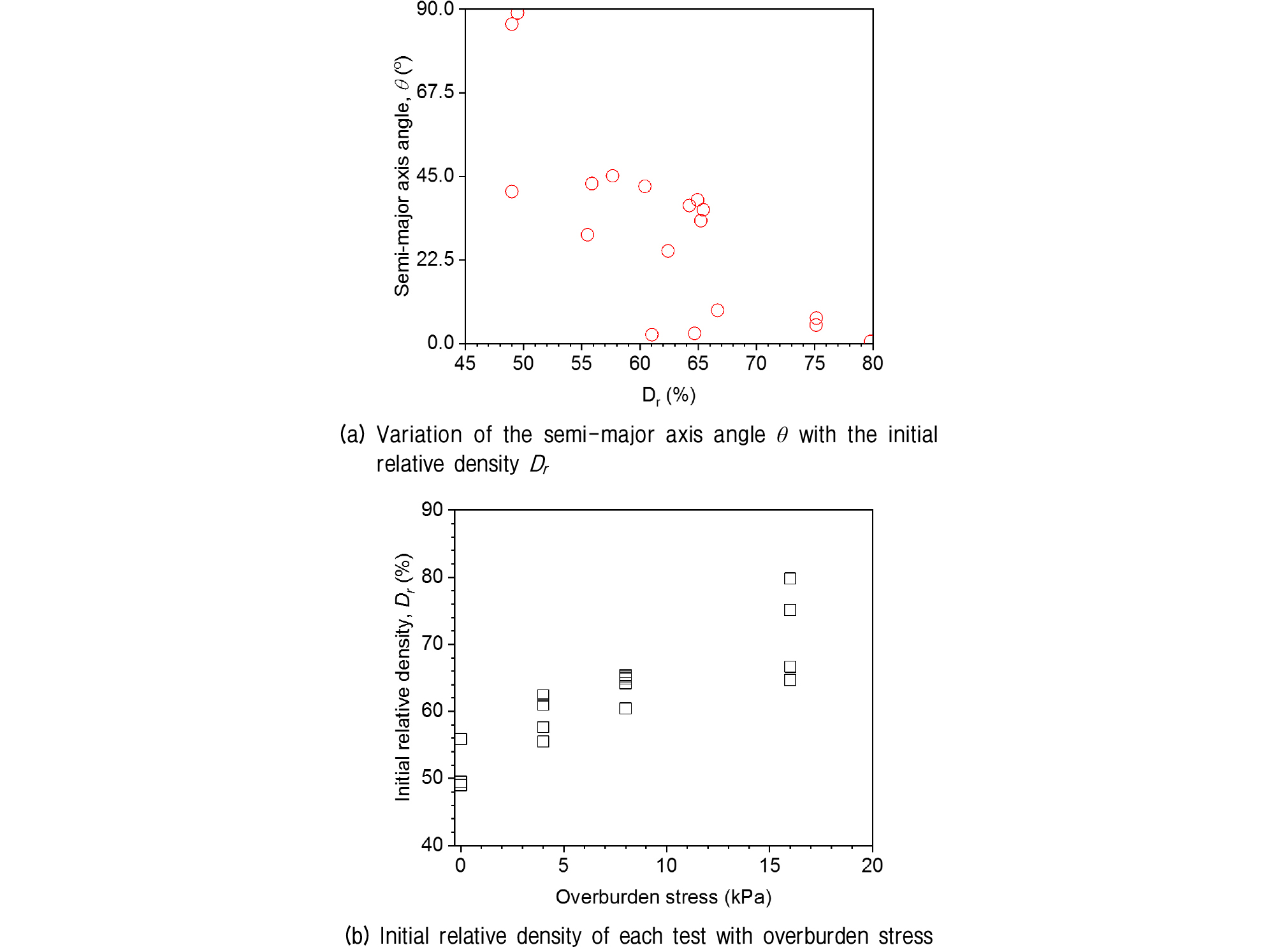
본 연구에서는 상부 응력에 따른 그라우트 구근의 팽창 방향의 변화를 수직축과 그라우트 구근 장축사이의 각도(θ)로 나타냈으며 그 결과는 Fig. 7(b)와 같다. 실험 결과 상부 응력이 증가할수록 θ값이 감소하여 16kPa의 상부 응력의 경우 평균 5°로 그라우트 구근이 수직방향으로 크게 팽창하는 것을 확인하였다(θ → 0°). 상부 응력이 없는 경우 그라우트 구근의 팽창 방향은 평균 θ 값이 65°였지만 그라우트 주입 유량에 따라 수평방향(θ → 90°)과 대각방향(θ → 45°)으로 나뉘었다. 또 상부 응력이 4, 8kPa로 증가하면서 평균 θ값은 각각 25°와 38°로 그라우트 구근이 대각 방향으로 팽창하는 현상을 확인하였다. 이러한 현상은 그라우트 구근의 중심의 이동으로 나타난다. 그라우트 팽창 영상을 토대로 그라우트 구근의 중심의 이동을 측정하였을 때 상부 응력이 없는 경우 그라우트가 수평방향으로 팽창하면서 수직방향 중심이동은 평균 0.49cm 상승이동을 보였다. 하지만 상부 응력이 높아짐에 따라 그라우트가 수직 방향으로 팽창하게 되고 그라우트 주입구 상부와 하부의 응력차이로 인해 4, 8, 16kPa의 경우에서 각각 평균 1.17, 1.04, 1.07cm 만큼 그라우트 구근의 중심이 상승하였다(Fig. 7(c)).

상부 응력이 매우 낮은 경우 주입구 근처 지반의 유효응력이 매우 낮고 상대 밀도 50%이하의 경우 수직 유효응력이 수평 유효응력보다 높아 수평 방향 압축성이 더 크다. 이로 인해 그라우트 구근이 상대적으로 압축이 잘 일어나는 수평방향으로 팽창한다. 하지만 유효응력이 증가함에 따라 상대밀도 65%이상의 지반에서는 지반의 압축률이 낮아 쉽게 압밀되지 않는다. 이러한 경우에는 인장 파괴 모드의 수압 파쇄 원리에 의해 구근의 팽창 방향이 결정된다. 따라서 최대 주응력(major principal stress)방향인 수직으로 인장 균열이 발달하며, 동시에 최소 주응력(minor principal stress) 방향인 수평방향으로는 구근이 팽창한다. 이러한 이유로 상대밀도가 높은 지반에서는 그라우트 구근이 수직방향으로 보다 빠르게 발달한다. 상대밀도가 50~65%인 지반의 경우 대각 방향으로 구근 팽창이 진행된다. 이러한 이유로 사질토 시료의 상대밀도가 낮은 경우 그라우트는 수평방향으로 팽창하지만 상대밀도가 높아짐에 따라 그라우트의 팽창 방향이 수직축에 가까워진다(Fig. 8).

Fig. 8

(a) Variation of the semi-major axis angle θ with the initial relative density D_r and (b) initial relative density of each test with overburden stress

3.3 업스케일링을 위한 고찰

본 실험 결과를 수평방향 대칭성을 이용해 현장 규모의 3차원으로 확장하면 그라우트 구근의 부피는 다음과 같다.

위의 식을 통해 현장의 응력 조건을 재현한 실험으로 주입 현장의 상부 응력과 그 조건에서 a/b값 및 구근 팽창 방향을 구한다면 주입한 구근의 부피(V)에 따른 구근의 수평·수직 직경을 알 수 있다. 예를 들어 본 연구의 σ16Q14 조건의 지반에 200L의 그라우트를 주입하는 경우 그라우트 구근의 팽창 방향이 수직방향이므로 수직 직경이 2a, 수평 직경이 2b가 된다. 또 그라우트 구근의 팽창 방향이 수직 방향이므로 식 (7b)를 통해 2a와 2b를 구하면 각각 766, 706mm가 된다. 이때 상부에 구조물이 없어 그라우트를 수직 주입 할 경우 그라우트 구근 간격은 766mm, 수평주입 할 경우 706mm가 된다. 하지만 σ00Q16 조건의 지반에 200L의 그라우트를 주입하는 경우 그라우트 구근의 팽창 방향이 수평 방향이므로 수직 직경이 2b, 수평 직경이 2a가 되며 Eq. (7a)에 의해 각각 645, 769mm가 된다. 이때 수직 그라우팅과 수평 그라우팅의 경우 구근의 간격은 각각 645, 769mm가 된다(Table 3). 주입공의 간격은 수직 그라우팅의 경우 수평 직경, 수평 그라우팅의 경우 수직 직경이 되며 이 값과 영향 반경(일반적으로 구근 직경의 2배), 중첩률을 고려하여 주입 간격을 설계할 수 있다.

4. 결 론

본 연구에서는 실내 압밀 그라우팅 실험을 통해 그라우트 수평 주입 과정을 촬영하고 상부 응력에 따른 그라우트 구근의 형상과 팽창 방향을 관찰하였다. 실험 결과 그라우트 구근은 일반적으로 가정하는 원형이 아닌 타원형 단면을 가지며 팽창하였으며 지반에 가해지는 상부 응력이 증가함에 따라 구근의 형상은 장축과 단축의 차이가 평균 1.1배에서 1.05배로 감소하여 원형에 가까워졌다. 또 그라우트 구근의 팽창 방향을 측정한 결과 상부 응력이 증가함에 따라 구근의 팽창 방향이 수평방향에서 수직방향으로 변하는 경향을 확인하였다. 이는 구근의 중심 이동으로 나타나며 높은 하중에서 그라우트 구근의 중심이 수직과 수평방향으로 크게 이동하였다. 이를 통해 상부에 구조물이 있는 지반에 수평 압밀 그라우팅 시공 시 주입구에 작용하는 응력 상태에 주입 간격, 수직·수평 영향 반경 등 보다 정확한 주입 전략을 세울 수 있을 것으로 사료된다.