1. 연구배경 및 목적
2. 수치해석
2.1 해석 프로그램 및 모델
2.2 해석조건
2.3 지반 물성치 및 구조물 제원
2.4 2차원과 3차원 수치해석 모델링
3. 유한요소 해석결과
4. 해석결과에 대한 분석 및 고찰
4.1 해석조건에 따른 최대 수평변위 관계
4.2 해석조건에 따른 최대 수평변위차 비율 관계
4.3 굴착규모에 따른 최대 수평변위차 비율 상관관계 분석
5. 결 론
1. 연구배경 및 목적
흙막이 굴착공사 주변 지반에서는 응력해방에 따른 변형이 발생하며, 그 거동 양상은 굴착 깊이, 굴착 폭, 지반 조건, 흙막이 공법, 공사 기간에 따라서 여러 양상으로 나타난다. 또한, 흙막이 구조물과 지반의 상호작용 효과가 동반 작용하는 경우와 같이 매우 복잡하게 고려해야 하는 요소들이 많아 흙막이 굴착에 따른 지반 거동의 정확한 예측을 어렵게 한다. 따라서 이렇게 복잡한 고려 요소들을 최대한 반영하여 지반 거동을 예측할 수 있는 현실적인 수단으로 수치해석에 의한 방법들이 보편적으로 인식되어 여러 연구자에 의해 꾸준하게 연구가 수행되었다.
St. John(1975)은 단단한 런던 점토에서의 무지보 정방형 굴착을 축대칭과 평면 변형조건에서의 2차원 해석뿐만 아니라 3차원 해석도 수행하였다. 그 결과, 2차원 해석이 3차원 해석보다 변형이 과도하게 예측된다고 하였다.
Naylor 등(1981)은 3차원 해석과 2차원 해석을 비교하였는데, 평면변형 해석 시 2차원 해석이 침하에 대해서는 비슷한 결과를 나타내지만 횡방향 변위는 3차원 해석이나 축대칭 해석에 비해 2배 정도까지 큰 결과를 나타내는 것으로 확인하였다.
Lin 등(2007)은 타이페이 101타워 건설 프로젝트에 대하여 대심도 굴착에 따른 벽체의 변위에 대한 거동을 연구하였는데 3차원 변형 해석결과 굴착심도에 따른 벽체의 수평변위는 계측결과와 비교적 유사하게 나타나 거동 예측에 있어 적용성이 우수하였으나 2차원 변형 해석결과는 이들 결과보다 거의 2배 정도까지 큰 수치의 변위를 보였다.
Kim(2007), Lee 등(2008)은 현장계측자료와 수치해석결과를 비교 분석한 결과 흙막이 벽체의 실제 거동특성을 3차원 수치해석방법이 보다 정확하게 예측하고 있는 것으로 나타났다.
Jeong 등(2016)은 흙막이 벽체의 거동분석 및 안정성 검토 시에는 지반의 기하학적인 비대칭성과 3차원 구조로 설치되는 흙막이 벽체 및 지보재의 특성을 고려한 3차원 수치해석 기법의 적용이 적절함을 확인하였다. 또한, 해석대상 지반이 암반에 비해 강성이 낮은 토사지반에 있어서 일정심도(20m) 이상의 지반굴착에 따른 흙막이 벽체의 거동분석을 위해서는 3차원 수치해석이 합리적인 것으로 판단하였으며, 보다 정확한 3차원 수치해석을 위해서 굴착 길이(L)의 해석영역을 일정범위(굴착심도의 2배) 이상으로 설정하는 것이 적합할 것으로 판단하였다.
기존 연구동향에서 보듯이 대부분 2차원 해석이 3차원 해석보다 변형이 과대하게 예측되며, 3차원 해석이 실제 거동특성과 유사하다는 것을 확인하였으나 2차원 해석과 3차원 해석을 다양한 조건에서 비교·분석한 연구의 부족으로 흙막이 벽체의 해석 시 일반적으로 적용되는 2차원 해석의 경우 굴착 폭이 작으면 토압에 의한 상호간섭이 발생하며, 그 영향으로 2차원 해석 시 굴착 폭이 작은 구간에서는 흙막이 벽체의 수평변위에 대한 신뢰성 있는 예측이 어렵다.
따라서 본 연구에서는 2차원 해석 시 토압에 의한 상호간섭 발생의 범위가 되는 굴착 폭의 경계를 확인하기 위하여 H-pile 토류벽체에 대하여 점성토, 사질토, 사질토 및 풍화암의 지층조건에서 다양한 조건의 굴착 깊이(H)와 굴착 폭(B)에 대하여 2차원 및 3차원 유한요소해석을 수행하여 각 조건에 따른 굴착 폭과 수평변위의 관계를 제시하고자 하였다.
2. 수치해석
2.1 해석 프로그램 및 모델
본 연구에서 이용한 프로그램인 GTS NX(MIDAS, 2017)는 유한요소해석법(FEM)을 기초로 하며, 지반의 탄소성 강도 특성 및 흙막이 벽체와 지지구조의 탄성 강도 특성을 고려하여 실제 현장과 유사한 응력-변형율 거동을 구현한다. 토압을 적용하는 대신 지반강도특성, 흙막이 벽체 및 지지구조의 탄성 강도 특성을 고려하여 응력-번형 거동을 구하는 방식으로 2차원 탄소성해석과는 기본 원리에서 차이가 있다. 또한, 벽체 및 흙의 거동을 나타내기 위하여 유한의 Interface 요소망을 생성하는데 이를 위하여 응력-변형율 관계가 필수적으로 요구되며, 본 연구에서는 흙막이 거동의 안정성 해석에 가장 적합한 지반구성 모델인 Mohr-Coulomb 탄소성모델을 적용하였다.
2.2 해석조건
본 연구의 수치해석에 적용된 해석조건의 Case는 굴착깊이 6.0m, 9.0m, 12.0m 3가지, 굴착 폭 4.0m, 6.0m, 8.0m 12.0m, 16.0.0m, 20.0m, 24.0m 7가지로 구분하였고, 지층조건은 굴착 배면과 저면 모두 점성토인 경우, 모두 사질토인 경우, 굴착저면 상부는 사질토 하부는 풍화암인 경우의 3가지 조건으로 구분하여 총 63가지 Case를 선정하였고, 각각의 Case에 대하여 2차원과 3차원 유한요소해석을 수행하였다. 또한, 해석의 간편화를 위하여 지하수위는 없는 것으로 적용하였다.
각 Case별 해석조건은 Table 1에 나타내었다.
Table 1.
Numerical analysis case
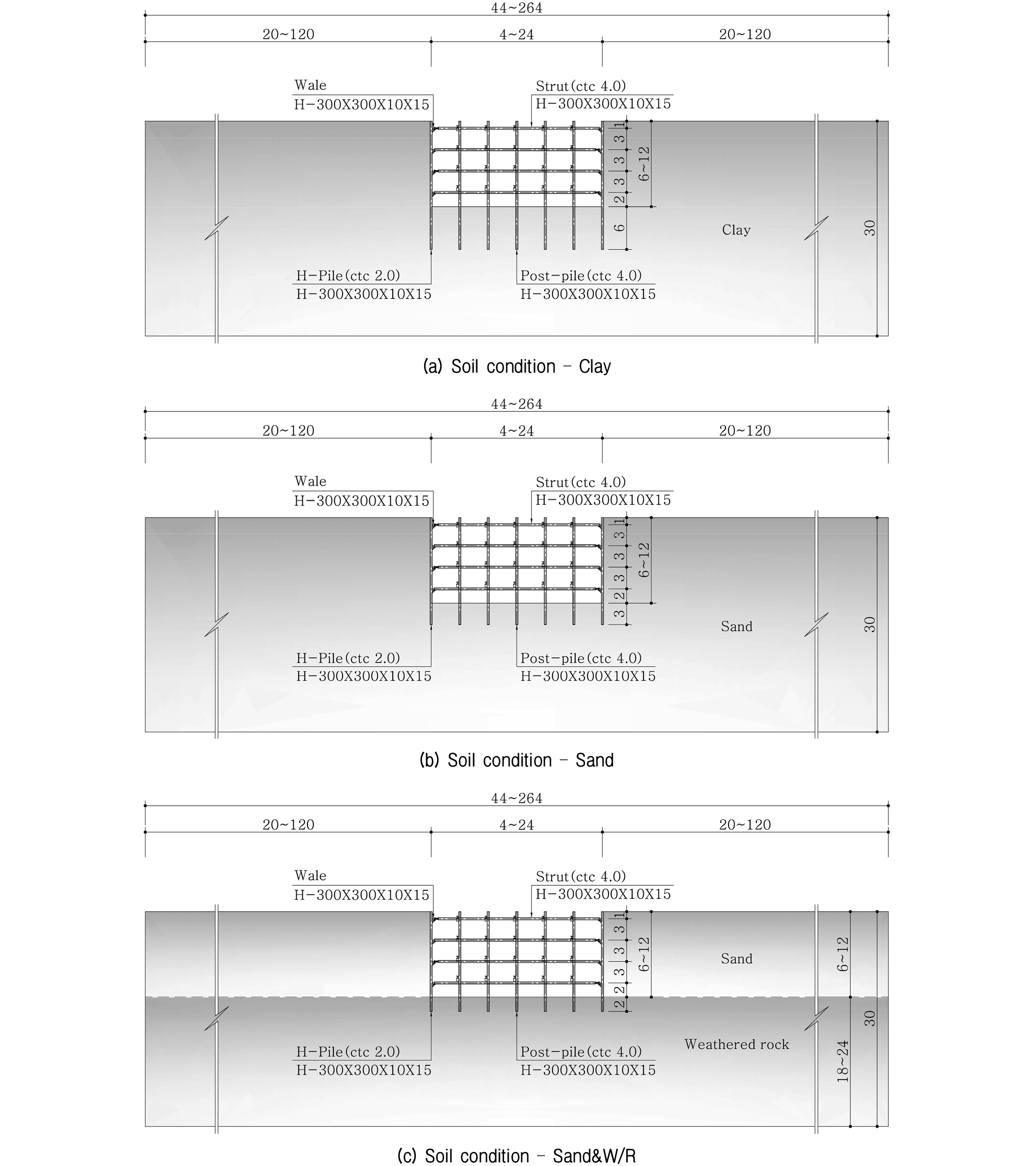
각각의 해석조건에서 모두 근입장에 대한 안정성을 확보하는 조건이며, 각 해석조건 Case에 대한 지층조건별 대표 해석단면은 다음의 Fig. 1과 같이 나타내었다.
2.3 지반 물성치 및 구조물 제원
흙막이 해석을 위한 지반정수는 문헌자료를 참고로 하여 일반적인 점성토, 사질토, 풍화토에 대한 값을 산정하였으며, 흙막이벽체는 연성벽체인 H-Pile 공법이며, 벽체, 버팀보, 띠장 모두 H-300×300×10×15 규격의 H-Pile을 적용하였다. 본 연구의 수치해석에 적용된 지반정수는 Table 2와 같고, 구조물의 제원은 Table 3과 같이 적용하였다.
Table 2.
Properties of soil
Table 3.
Material properties of structural members
2.4 2차원과 3차원 수치해석 모델링
2차원과 3차원의 유한요소에 필요한 해석범위는 굴착 폭과 굴착 깊이의 영향을 고려하고, 경계조건 구속의 영향을 최소화하기 위하여 2차원은 수평방향 굴착부 후면은 좌우로 굴착 폭의 5배로 20.0∼120.0m, 수직방향은 최대 굴착 깊이의 2.5배인 30.0m로 경계범위를 설정하였다.
3차원 해석의 지반 굴착은 정방형 형태로 X, Y방향을 동일하게 굴착하는 것으로 모델링하였고, 흙막이 벽체의 모델링 경계조건은 X-Y 평면상에서 좌-우측 변형을 구속하였으며, 굴착 저면부는 수직방향 변위를 구속하고, 측벽 및 중간말뚝의 Z방향 회전을 구속하는 조건으로 하였다.
경계면에는 경계면요소(Interface Element)를 사용하여야 하나 본 연구목적이 지반 굴착폭에 따른 벽체의 수평변위 등에 대한 정성적 거동의 일반적 경향성을 보기 위함이므로 지반경계면 요소에 따른 변위 차이는 발생되지 않도록 경계면요소(Interface element)는 사용하지 않고 단순화하여 수치해석을 실시하였다.
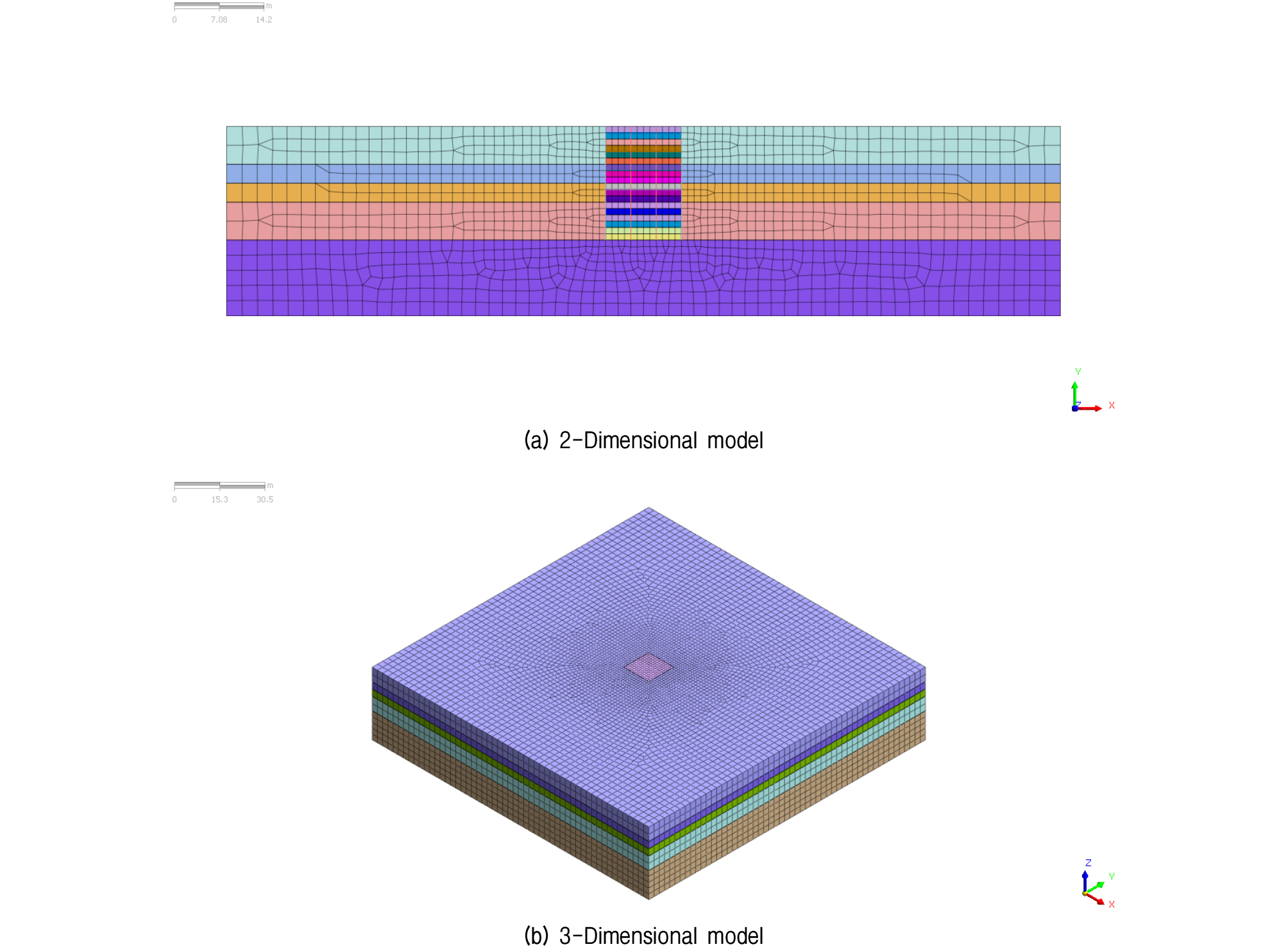
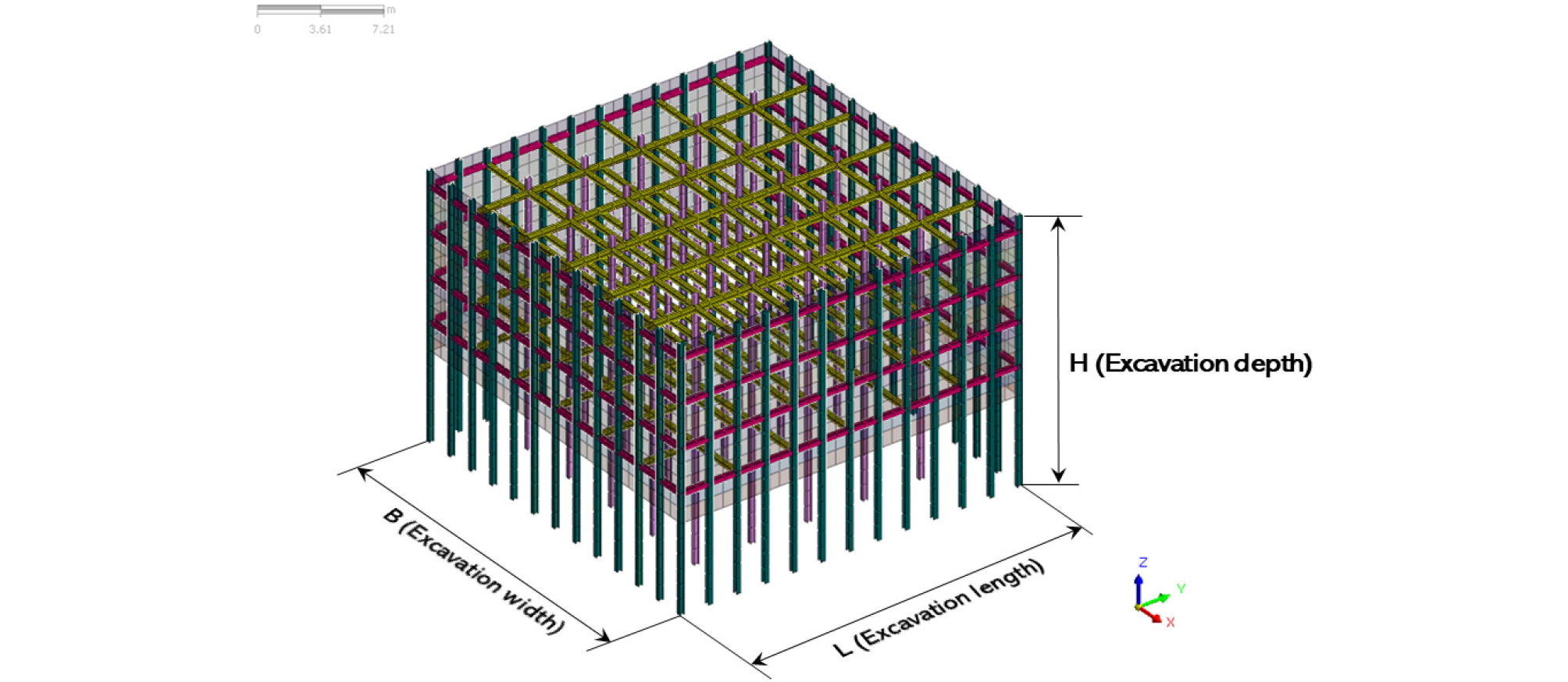
본 연구의 수치해석을 위한 2차원과 3차원의 대표적인 유한요소 해석 모델링은 다음의 Fig. 2에 나타내었으며, 3차원 수치해석의 대표적인 정방형 형태 구조적 모델링은 Fig. 3에 도식적으로 표현하였다.
3. 유한요소 해석결과
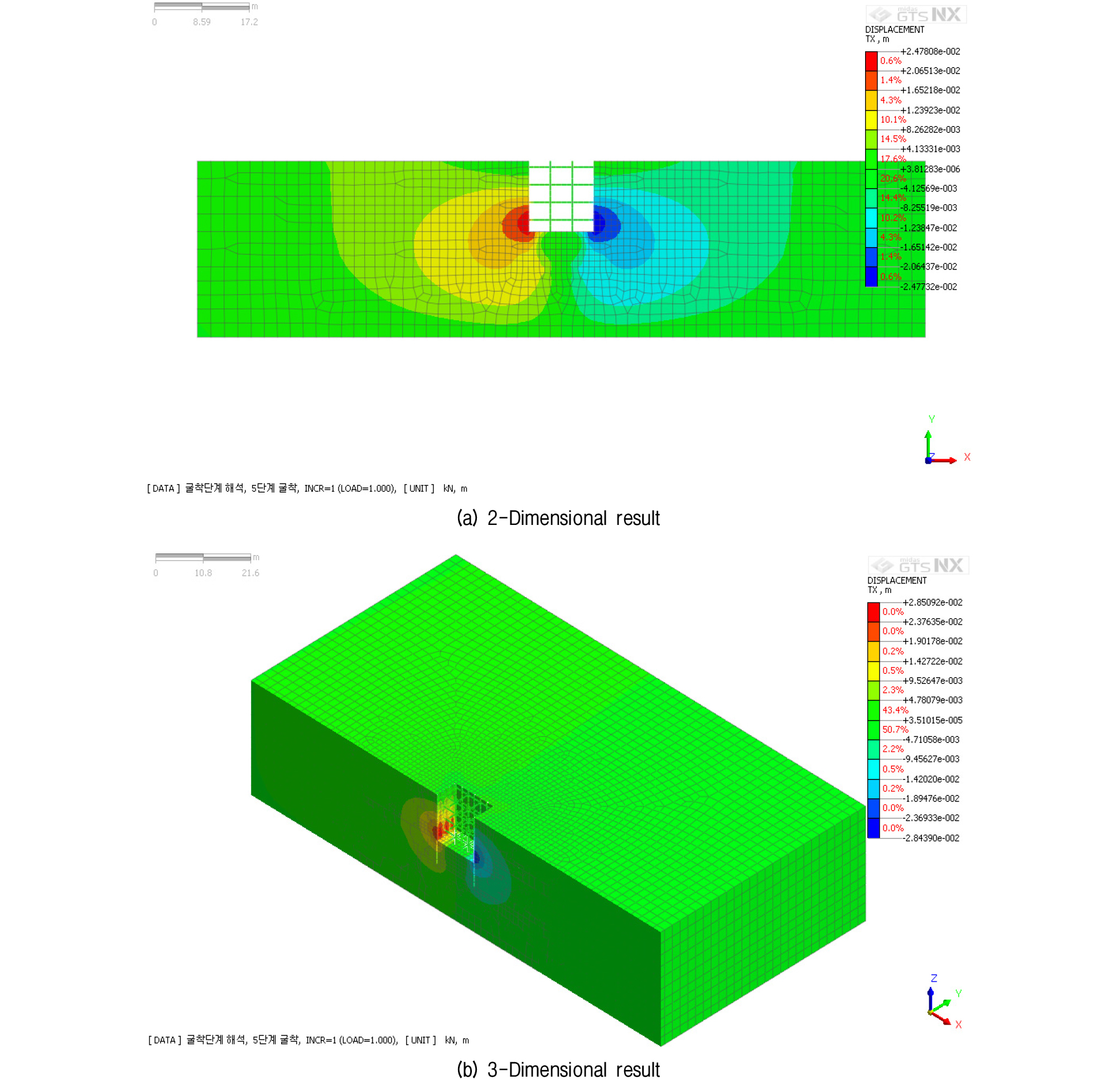
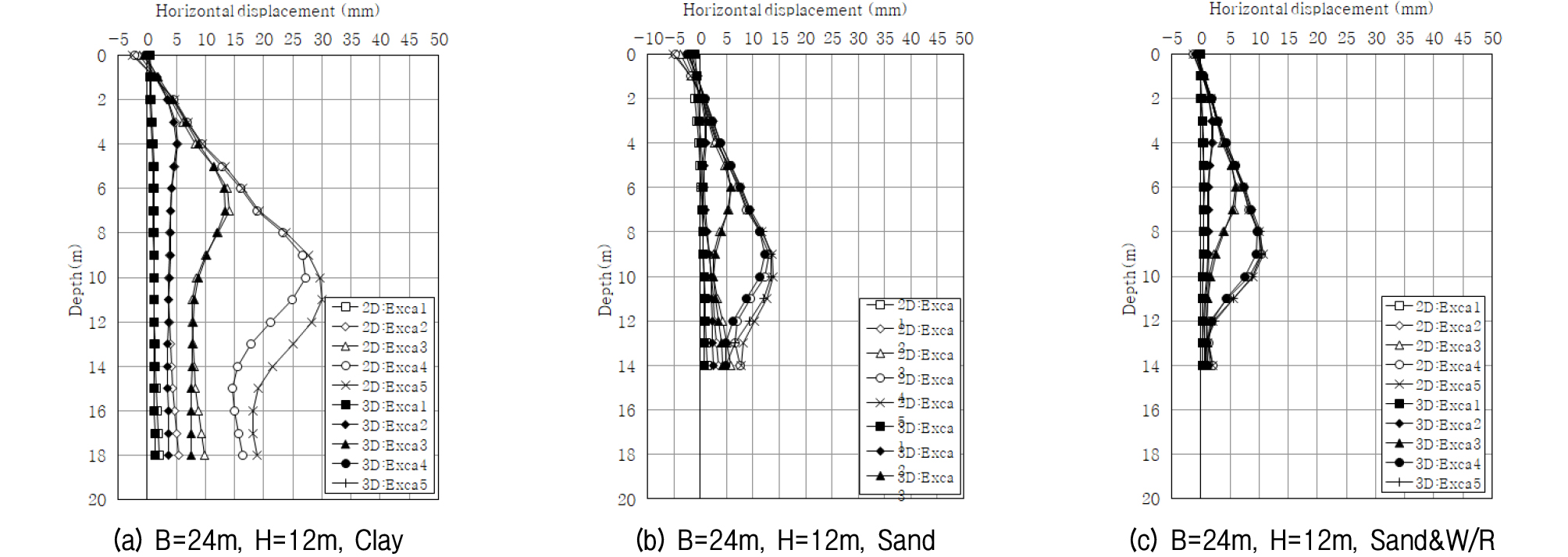
조건별 해석을 통하여 2차원 및 3차원에 대한 유한요소해석 결과를 도출하였고, 수평변위에 대한 유한요소해석 결과에서 굴착 폭별 최대심도의 대표적인 해석결과를 2차원 해석과 3차원 해석으로 구분하여 Fig. 4와 같이 나타내었다.
2차원과 3차원의 흙막이 벽체의 굴착 깊이에 따른 대표적인 수평변위 해석결과를 Fig. 5에 나타내었다.
최대 수평변위의 발생 깊이는 Table 4와 같으며, 이를 살펴보면 최대 수평변위의 발생깊이는 전반적으로 굴착 깊이의 50.0∼83.3% 위치에서 발생하는 것을 확인하였다. 최대 수평변위는 굴착 깊이가 깊어질수록 하부에서 발하였으며, 점토→사질토→사질토&풍화암으로 토성이 변경되면서 상부에서 발생하였다.
Table 4.
Max. horizontal displacements (H=6.0m)
유한요소해석에 의한 흙막이 벽체의 굴착 폭별 최대 수평변위 해석결과를 굴착 깊이와 지층조건별로 분석하여 Table 5∼7에 나타내었다.
Table 5.
Max. horizontal displacements (H=9.0m)
Table 6.
Max. horizontal displacements (H=12.0m)
Table 7.
Position of maximum horizontal displacement
해석결과 전체 최대 수평변위 발생은 해석조건 모두 굴착 깊이가 증가할수록, 굴착 폭이 증가할수록, 사질토&풍화암-사질토-점성토 순으로 크게 나타났다. 또한, 최대 수평변위도 2차원 해석 값이 3차원 해석 값보다 크며, 그 차이도 대체로 굴착 깊이가 증가할수록, 사질토&풍화암-사질토-점성토 순으로 크게 나타났다. 반면 굴착 폭이 증가할수록 최대 수평변위의 2차원 해석 값과 3차원 해석 값의 차이는 감소했으며, 2차원 해석 값 대비 3차원 해석 값의 비율에서도 2차원 해석 값과 3차원 해석 값의 격차가 감소했음을 확인할 수 있었다.
4. 해석결과에 대한 분석 및 고찰
2차원과 3차원 유한요소 해석결과를 통하여 흙막이 벽체의 수평변위에 대한 해석조건의 구성인자인 굴착 폭, 굴착 깊이, 지층조건에 따른 상관관계를 분석하고 고찰하였다.
4.1 해석조건에 따른 최대 수평변위 관계
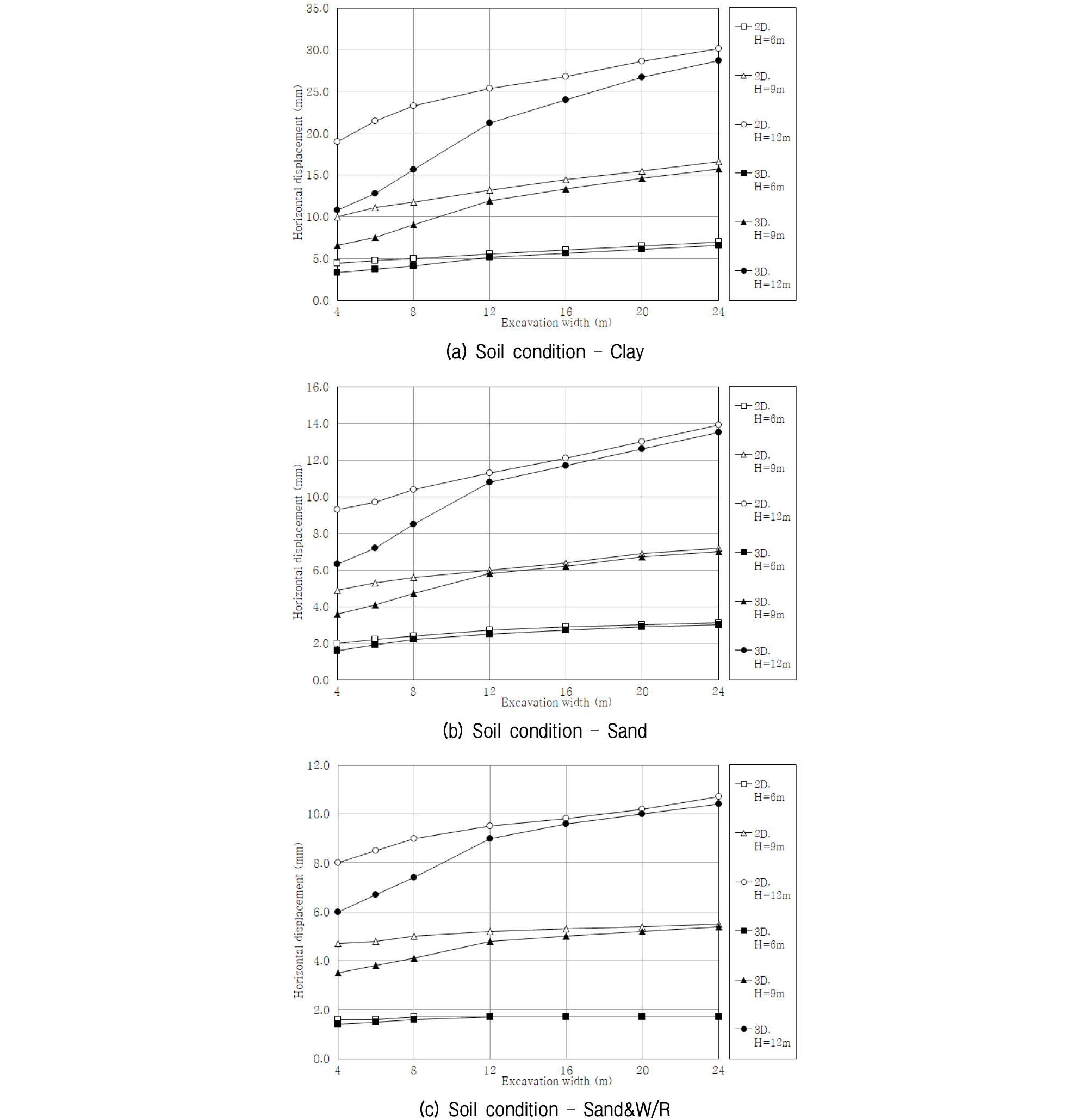
흙막이 벽체의 굴착 깊이에 따른 최대 수평변위 해석결과를 지층 조건별로 굴착 폭에 따라 분석하여 Fig. 6에 나타내었다.
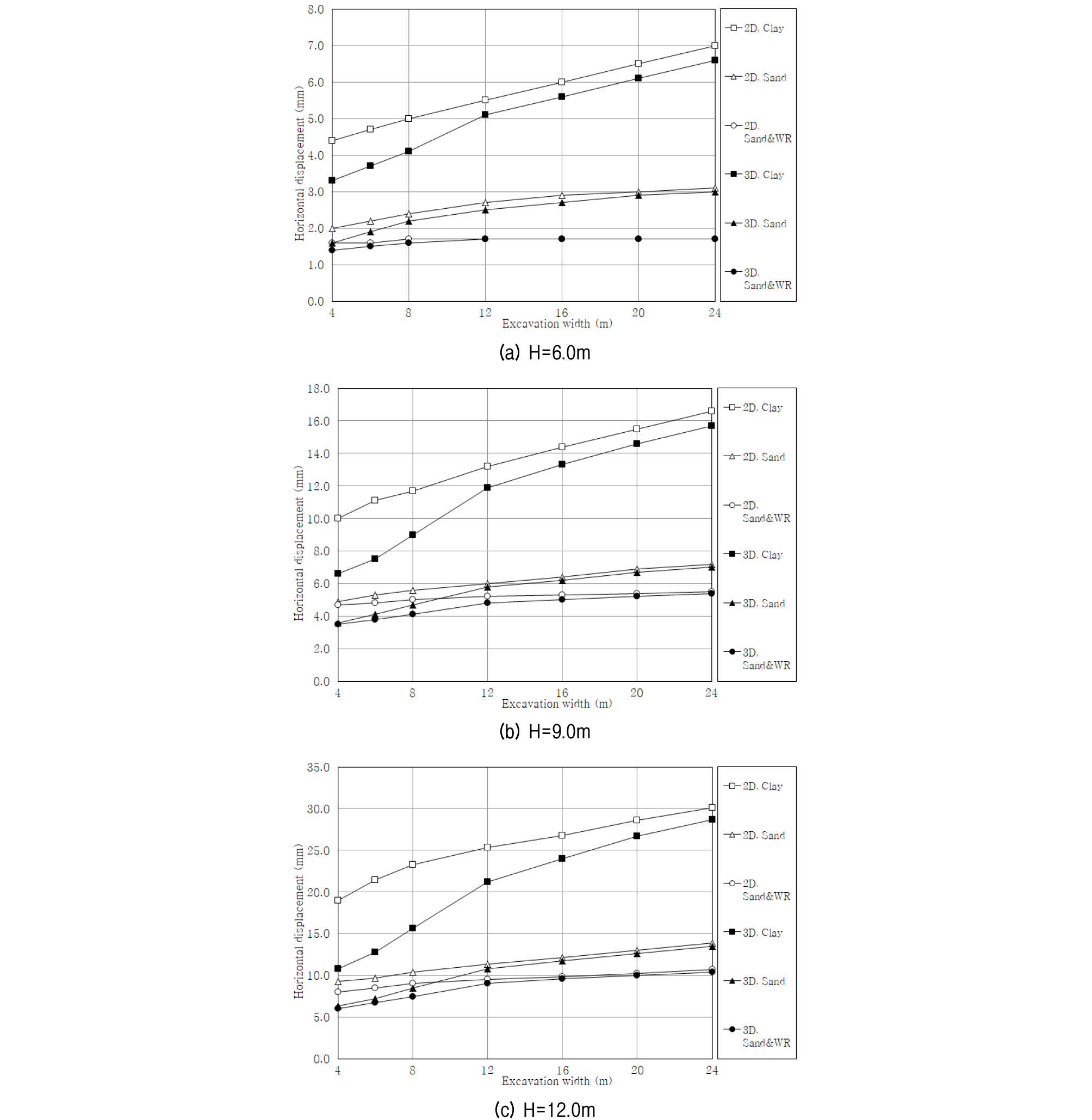
흙막이 벽체의 지층 조건에 따른 최대 수평변위 해석결과를 굴착 깊이별로 굴착 폭에 따라 분석하여 Fig. 7에 나타내었다.
해석조건에 따른 최대 수평변위 관계를 살펴보면 2차원 해석 값과 3차원 해석 값의 최대 수평변위 차이는 대체로 굴착 깊이는 증가할수록, 지층조건은 사질토&풍화암-사질토-점성토 순으로 크게 나타났다. 굴착 폭에 따른 최대 수평변위의 변화 경향성을 살펴보면 굴착 폭이 작은 10.0m이하 구간에서는 2차원보다는 3차원 해석 값 증가가 급격하며, 굴착 폭이 10.0m이상으로 커지면서 2차원 해석 결과와 격차가 작아지면서 값이 비슷해졌다. 2차원과 3차원 해석 값의 최대 수평변위 격차는 굴착 폭이 작고, 굴착 깊이가 증가할수록 크게 나타났으며, 전반적으로 굴착 폭 10.0∼15.0m 구간에서 2차원과 3차원의 격차가 감소하여 수렴하는 경향이 나타났다.
전반적으로 3차원 해석 값보다 2차원 해석 값이 크게 나타나는 것은 2차원 해석이 평면변형율 조건으로 해석되기 때문이며, 토압에 의한 상호간섭이 발생하는 굴착 폭이 작은 구간에서 그 경향성이 크게 나타났다.
또한, 사질토층과 사질토&풍화암층의 지층조건에서는 2차원 해석과 3차원 해석의 최대 수평변위가 비교적 작고, 미소하여 분석결과의 수치적 의미보다는 경향성만을 참고하는 것이 합리적일 것으로 판단된다.
4.2 해석조건에 따른 최대 수평변위차 비율 관계
굴착 폭에 따른 수렴 경향을 명확하게 구분하기 위하여 최대 수평변위차 비율(δ(2D-3D)/H, %)을 통한 분석을 실시하였다.
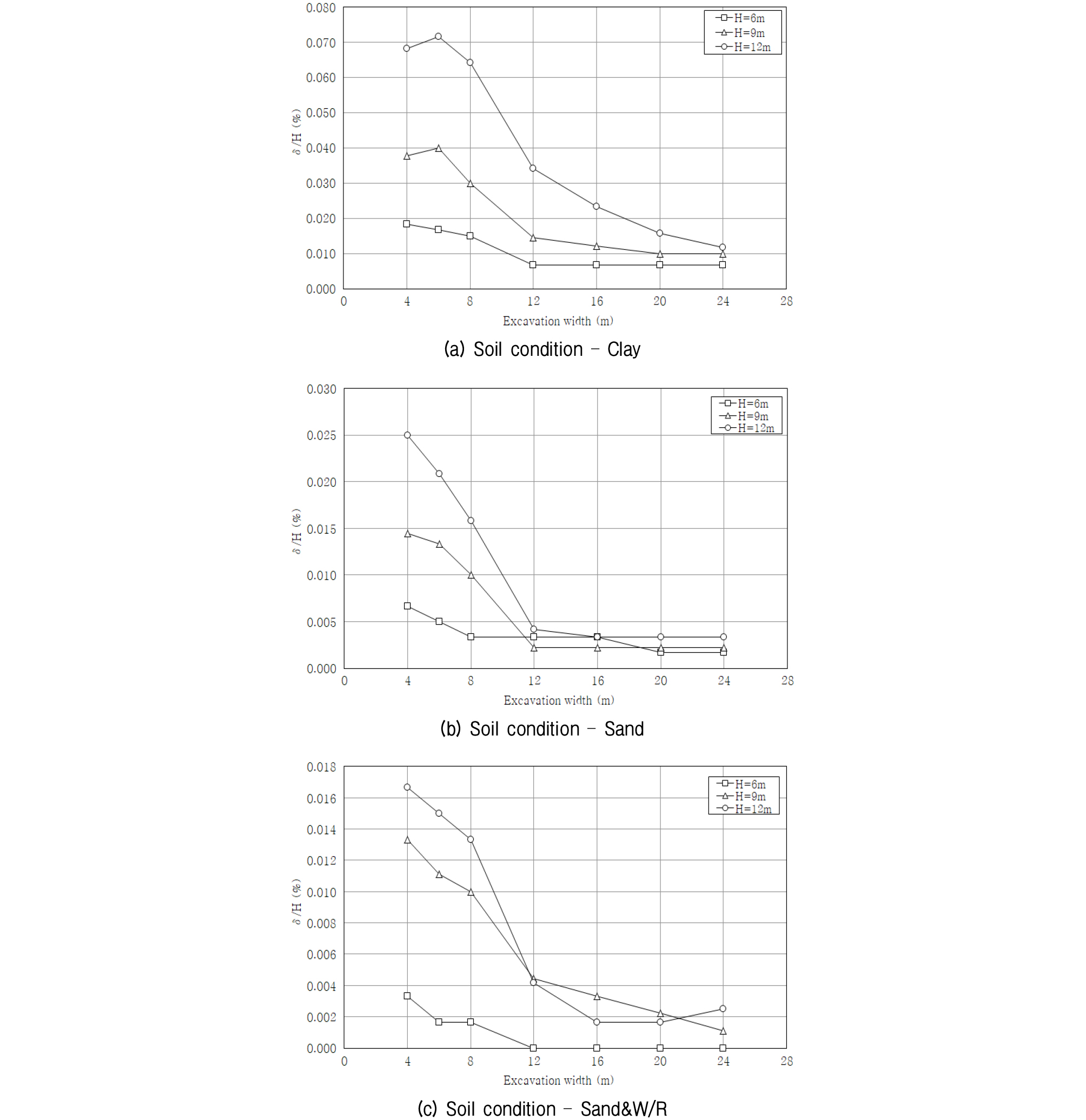
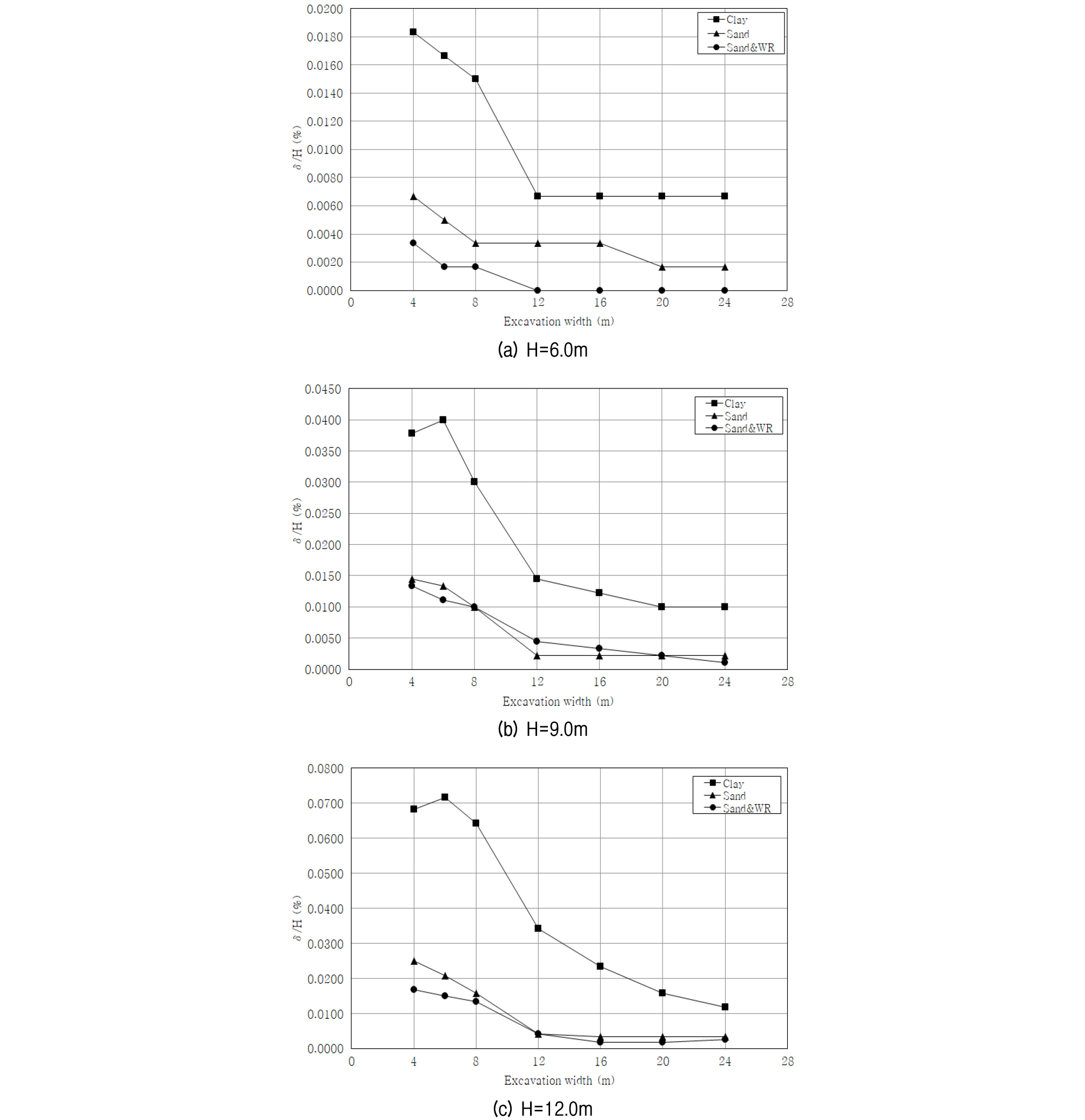
흙막이 벽체의 굴착 깊이에 따른 최대 수평변위차 비율(δ(2D-3D)/H, %)의 상관관계 분석결과는 Fig. 8에 나타내었다.
흙막이 벽체의 지층조건에 따른 최대 수평변위차 비율(δ(2D-3D)/H, %)의 상관관계 분석결과는 Fig. 9에 나타내었다.
최대 수평변위차 비율(δ(2D-3D)/H, %)의 굴착 폭 수렴구간을 분석하면 점성토는 굴착 폭 12.0∼16.0m 구간, 사질토는 굴착 폭 8.0∼12.0m 구간, 사질토&풍화암에서 굴착 폭 12.0∼16.0m 구간에서 수렴의 경향성을 보이기 시작하였다. 단, 점성토 굴착깊이 12.0m는 굴착 폭 24.0m 이상에서 최대 수평변위차 비율이 수렴될 것으로 판단된다.
이러한 굴착 폭(B)에 따른 최대 수평변위차 비율의 수렴 경향성을 통하여 2차원 해석 시 토압에 의한 상호간섭을 발생시키는 굴착 폭의 범위를 확인할 수 있었다.
4.3 굴착규모에 따른 최대 수평변위차 비율 상관관계 분석
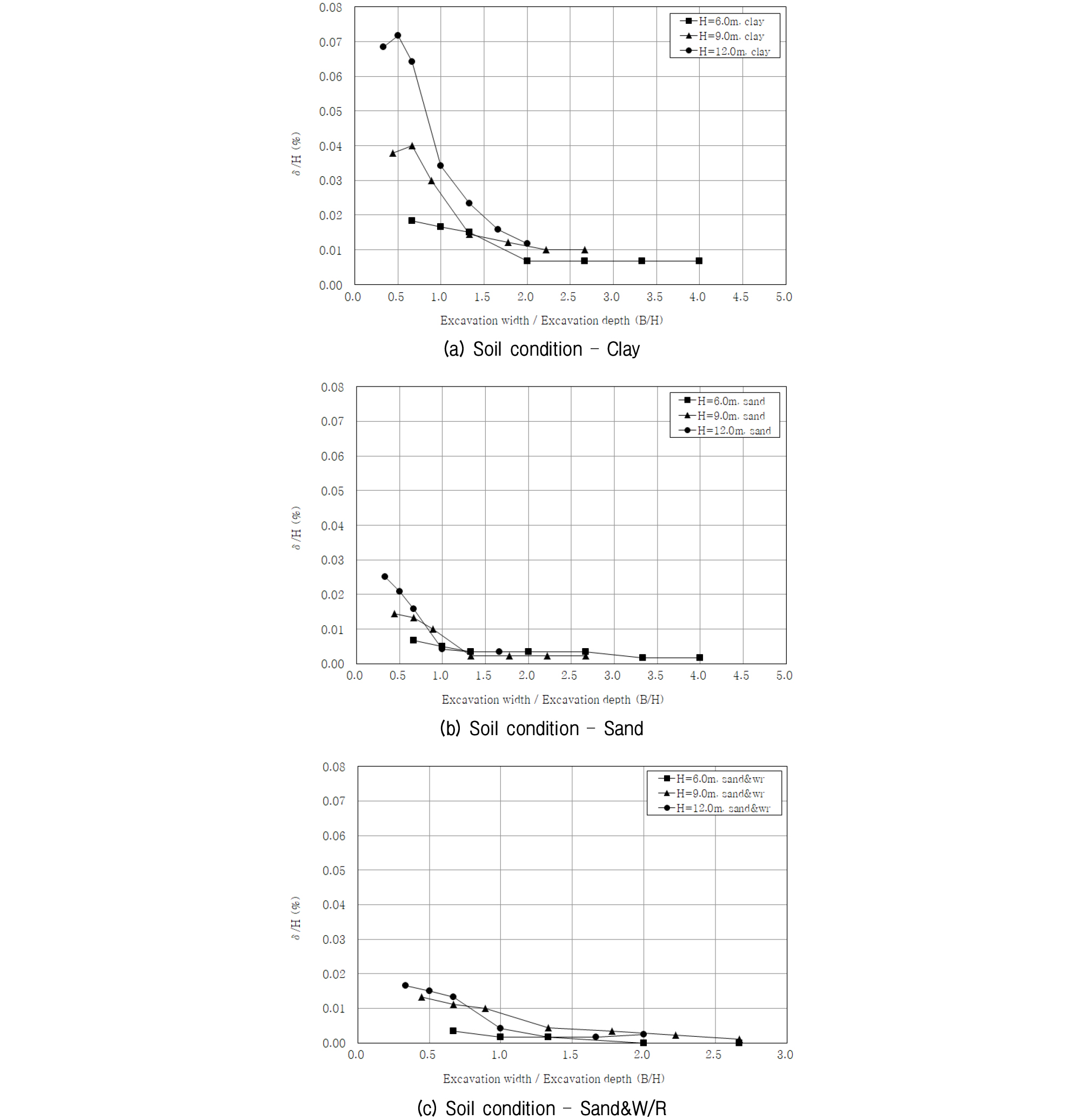
굴착 폭(B)과 굴착 깊이(H)에 따른 최대 수평변위차 비율(δ(2D-3D)/H, %)에 대한 분석을 보다 객관화하고, 해석조건 관계를 단순화시키기 위하여 굴착규모(B/H)의 개념을 적용하여 분석하였다. 굴착규모(B/H)에 따른 최대 수평변위차 비율(δ(2D-3D)/H, %) 상관관계 분석결과를 Fig. 10에 나타내었다.
굴착규모(B/H)를 고려한 최대 수평변위율(δ(2D-3D)/H, %)의 굴착규모(B/H) 수렴구간을 분석하면, 점성토에서는 굴착규모(B/H) 2.0∼2.2, 사질토에서는 굴착규모(B/H) 1.3, 사질토&풍화암에서는 굴착규모(B/H) 1.0∼1.3에서 수렴의 경향성을 보였다.
이러한 굴착규모(B/H)에 따른 최대 수평변위차 비율(δ(2D-3D)/H, %)의 수렴 경향성을 통하여 2차원 해석 시 토압에 의한 상호간섭을 발생시키는 굴착 규모의 범위를 확인할 수 있었다.
5. 결 론
본 연구에서는 2차원 해석 시 토압에 의한 상호간섭 발생의 범위가 되는 굴착 폭의 경계를 확인하기 위하여 H-pile 토류벽체에 대하여 다양한 조건의 굴착 깊이(H)와 굴착 폭(B)에 대하여 2차원 및 3차원 유한요소해석을 수행하여 각 조건에 따른 굴착 폭과 수평변위의 상관관계를 연구하였으며, 그에 대한 결과를 다음과 같이 제시하였다.
(1) 최대 수평변위와 최대 수평변위율(δ(2D-3D)/H, %)의 분석결과 굴착 폭 및 굴착 깊이의 증가에 따른 수치 및 형태의 차이보다는 지층조건에 따른 차이가 더 크게 영향을 미쳤다. 특히, 수평 변위가 비교적 크게 발생하는 점성토에서만 굴착 폭에 따른 해석적 경계를 뚜렷하게 구분할 수 있었고, 사질토층과 사질토&풍화암층의 경우는 수평변위가 자체가 미소하여 분석결과의 수치적 의미보다는 경향성만을 참고하는 것이 합리적일 것으로 판단된다.
(2) 수평변위가 굴착 폭이 작은 구간에서는 3차원 해석 값에 비하여 2차원 해석 값이 보다 크게 나타나는 것은 2차원 해석이 평면변형율 조건으로 해석되기 때문이며, 또한 2차원 해석 시 토압에 의한 상호간섭이 발생하는 굴착 폭(B) 이내의 구간에서는 신뢰성 있는 벽체의 수평변위를 예측하기 위하여 2차원 해석 대신 실제 거동과 유사한 3차원 해석을 하는 것이 합리적일 것으로 판단된다.
(3) 따라서, 점성토의 경우 굴착규모(B/H) 2.0 이하와 굴착 깊이 10m 이하에서 굴착 폭(B)이 12m보다 작고, 굴착 깊이(H) 10m 이상에서 굴착 폭이 24m보다 작으면 3차원 해석을 하는 것이 합리적이며, 굴착규모(B/H) 2.0 이상과 굴착 깊이 10m 이하에서 굴착 폭(B)이 12m보다 크고, 굴착 깊이(H) 10m 이상에서 굴착 폭(B)이 24m보다 크면 2차원 해석을 적용하는 것이 합리적일 것이라 판단된다.
(4) 본 연구의 결과는 제시된 해석 모델과 조건에 대한 제한적 결과로서 해석적 한계가 있을 수 있으므로, 실제 적용 시는 이러한 점을 고려하여 최소한의 자료로 활용해야 할 것이다.
또한, 추후 다양한 지반 구성모델과 경계면 요소, 벽체의 강성 등에 관한 해석적 연구와 국내의 다양한 실제 현장들의 규모 및 결과의 활용과 연계된 연구가 추가로 필요할 것으로 판단된다.