1. 서 론
2. 탄소성 해석을 이용한 원형가물막이 구조 안정성 검토 방법
2.1 탄소성 해석
2.2 Plane-Strain 조건과 Axial-Symmetry 조건의 상호 관계
2.3 반단면 변위 검토(Axial-Symmetry)를 이용한 원형가물막이의 탄소성 해석 적용
3. 3차원 유한요소해석을 통한 형상 및 크기에 따른 가물막이 단면 특성 검토
3.1 유한요소법의 3차원 해석 효과
3.2 유한요소해석 모델링 및 검토 결과
4. 결 론
1. 서 론
국내에서 최근 들어 지하대심도 굴착 공사가 많이 이루어 지고 있으며, 지하 장대터널 공사시 지하 작업을 위한 수직구, 비상탈출용 수직구 또는 환기구 등이 필요하다. 또한, 댐 취수탑 공사를 위한 차수벽체, 그리고 하천/하상 교량 공사시 교량기초 설치를 위한 가시설로서 원형 단면의 가물막이 적용이 널리 사용되고 있다. 하천이나 하상에서 이루어지는 공사들의 경우 공사비가 고가로서 경제적인 시공을 위해서는 합리적인 설계가 필요하다. 가물막이 구조물의 경우 일반적으로 임시 구조물임에도 불구하고 파괴 시 인명 및 장비의 피해는 물론 차수 및 복구공사로 인한 경제적 손실과 사회적 파급효과가 커 영구시설에 상응하는 안정성 확보가 필요하다. 이에 설계에서 가물막이 안정성 검토를 위한 해석 방안에 대한 검증 및 형상에 따른 구조적 특성을 확인하는 것은 중요한 일이다. 이러한 가물막이의 효율적인 시공, 관리를 위해서 지반굴착에 따른 흙막이 벽체에 대한 안정성 검토는 많은 연구자들(Terzaghi, 1920; Terzaghi and Peck, 1967; Clough and O’Rourke, 1990; Briaid and Kim, 1998)에 의해 이루어져 왔으며, 국내에서 원형 수직터널에 작용하는 토압 관련(Shin, 2004; Kim et al., 2009) 하여서도 선행연구가 활발하게 이루어지고 있는 것으로 확인하였다.
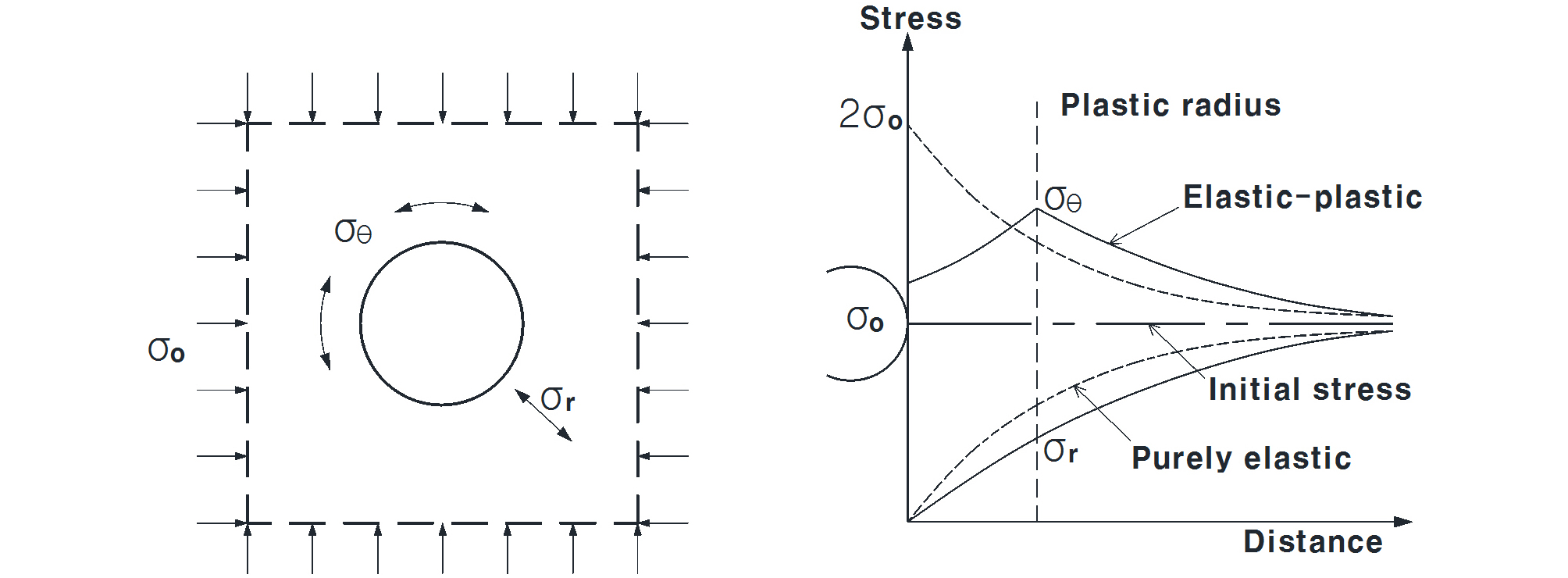
앞서 언급하였듯이 근래 원형단면의 가물막이 또는 차수벽 적용이 많이 되고 있는데 이는 원형단면에서 발생하는 아칭효과로 인하여 벽체에 작용하는 토압이 훨씬 감소하는 장점이 있기 때문이다(Szechy, 1966). Terzaghi와 Peck(1967)은 “아칭효과는 전단응력에 의해 발생하며 주변지반보다 과도한 변위를 받은 흙입자가 항복상태에 도달하여 주변지반으로 응력을 전달함으로써 전체적으로 응력이 재분배되고 항복상태에 도달한 토체의 응력이 작아지는 현상”이라고 설명하였다. Fara와 Wright(1963)는 Fig. 1과 같이 원형수직구를 굴착하게 되면 처음에는 반경방향응력 σr과 접선방향응력 σθ가 초기응력 σo와 같지만 굴착 후 굴착면 주변지반 입자가 이동하면서 탄성거동 시에는 반경방향응력 σr은 감소하고 접선방향응력 σθ는 증가하게 된다. 지속적인 응력이완이 발생하면 탄소성 거동을 일으키고, 이 때 접선방향응력 σθ는 탄성영역에서는 더욱 증가하고 소성영역에서는 다시 감소하게 됨을 수학적으로 증명하였다.
2차원 탄소성 해석을 이용한 수치해석방법은 지층의 변화, 흙막이 벽체 및 지지구조를 표준화하여 해석하므로 부재에 대한 각각의 부재력이 정확하게 산출되지 못하는 점이 있다. 특히 폐합단면 구조의 흙막이 구조에서 벽체의 모서리 구간과 중앙부의 변위 및 지반변형에는 큰차이가 있으며, 이에 따라 평면 변형률 조건의 2차원 수치해석을 통한 흙막이 벽체의 변위 및 지반변형은 3차원 해석결과와 비교하여 크게 나타나고 있다(Finno et al., 2007).
이에 본 연구에서는 일반적으로 원형가물막이의 안정성 검토를 위해 탄소성해석 적용시 원형보강재(ring beam)의 경우 지간을 직경 제곱에 비례하는 관용적인 방법(재료역학의 응력-변형률 관계에서 도출, 2.2절 참조)과 비교하여 흙막이 벽체(원형가물막이)의 원형보강재에 대해 평면 변형률 조건의 2차원 유한요소해석을 적용하여 원형보강재의 반단면 변위검토를 수행하여 지반반력계수(k)를 직접 산정하였고, 이를 탄소성해석에 적용하여 부재력을 검토하였다. 추가적으로 3차원 유한요소해석을 수행하여 가물막이의 형상 및 크기에 따른 역학적 특성을 확인하고자 형상(원형, 정사각형, 그리고 팔각형) 및 크기(직경 5m, 10m, 15m) 차이에 따른 거동 특성을 확인하고자 하였다.
2. 탄소성 해석을 이용한 원형가물막이 구조 안정성 검토 방법
2.1 탄소성 해석
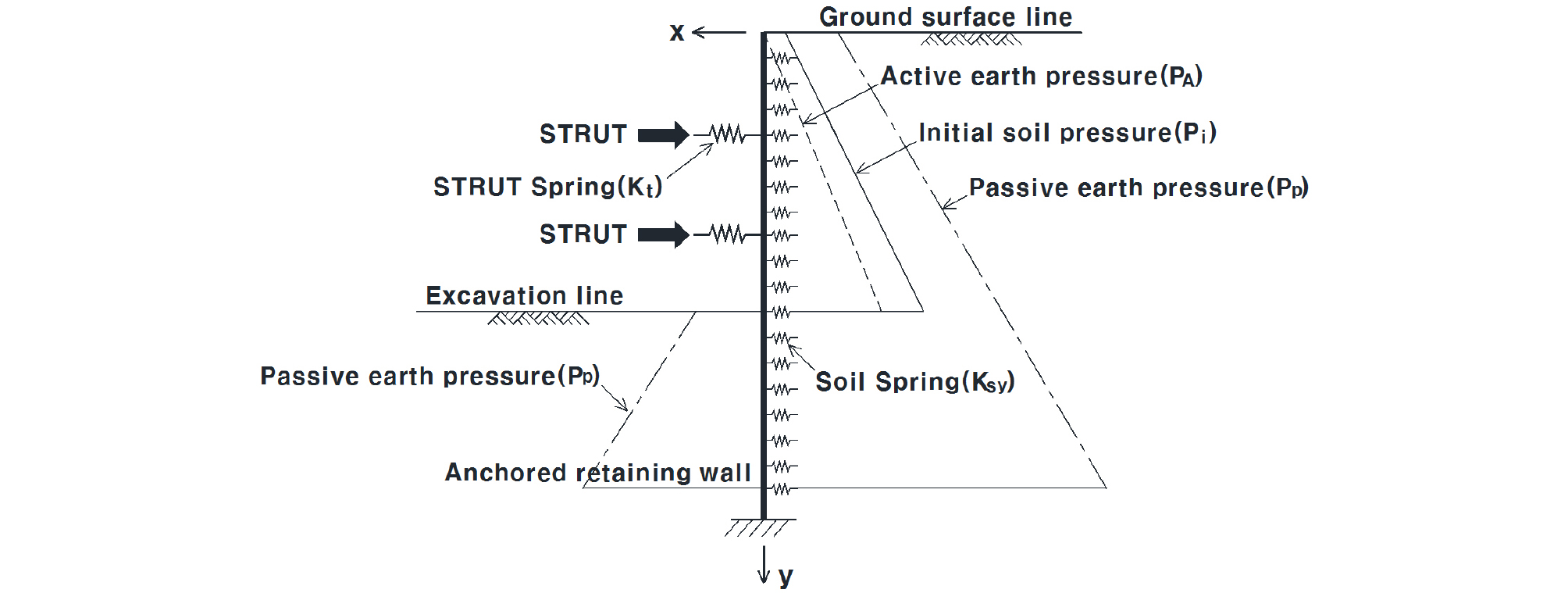
지반굴착을 위한 흙막이 구조물의 설계 및 해석방법에는 간편해석법, 탄소성법, 유한요소법 및 유한차분법의 수치해석방법 등이 있으며, 현재 국내에서는 탄소성법과 수치해석방법이 일반적으로 사용되고 있다(Jang, 2002). 흙막이 벽체의 검토 방법 중 탄소성법은 비교적 해석이 간편하여 흙막이 벽체 설계시 많이 사용되고 있는 해석방법으로 탄성 지반위의 보에 대한 해석 모델링은 Hetenyi(1946)에 의해 이론해가 제안되었으며, 유한차분법의 기술을 접목시키고, 지반을 탄소성의 스프링으로 치환하여 탄소성보 해석 방법으로 발전하였으며(Kim, 1998) 탄소성보 해석법은 토류벽체의 변위, 휨모멘트, 토압분포 등을 구할 수 있고 유한요소해석에 비해 입력자료가 간편한 장점으로 인하여 널리 사용되고 있는 방법이다(Haliburton, 1968; Briaid and Kim, 1998). Fig. 2와 같이 흙막이 벽체는 탄성보, 지보공은 탄성 Spring, 또 지반은 탄소성 Spring으로 모델링하고 초기 토압을 가하여 발생하는 변위를 계산하고 그 변위에 상응하는 지반의 탄소성상태를 판단하고 토압을 보정하여 다시 변위를 계산하는 반복과정을 통하여, 흙막이 벽체의 변위, 응력 및 지보공의 반력을 계산하는 해석법이다. 굴착에 따라 Rankine 또는 Coulomb 토압, Peck 등의 경험토압을 적용할 수 있다(Korea Rail Network Authority, 2011). 그러나 기존 연구결과에 따르면 탄소성 해석법은 각 해석 절점의 구조물과 지반의 저항력을 동시에 고려할 수 없어서 해석의 연속성 및 지반-구조물의 상호작용은 고려 할 수 없는 단점을 가지고 있다(Jeong et al., 2003; Jeong and Kim, 2009).
유한요소법 및 유한차분법과 같은 수치해석방법은 토압을 사용하는 대신에 응력-변형률 구성방정식을 이용하여 지반의 탄소성 강도특성과 흙막이 벽체 및 지지구조의 탄소성 강성을 고려함으로써 응력-변형 거동을 구한다. 벽체와 흙과의 거동을 나타내기 위해서는 대상지반 및 흙막이 벽체의 거동을 정확히 나타낼 수 있는 응력-변형률 관계가 필수적으로 요구되며, 지반 및 흙막이 구조물의 합리적인 모델링 및 해석에 필요한 제반 정수들의 정확한 추정이 해석결과의 타당성에 큰 영향을 미치게 된다.
2.2 Plane-Strain 조건과 Axial-Symmetry 조건의 상호 관계
원형가물막이의 탄소성해석시 원형띠장(ring beam)의 경우 Plane-Strain 조건 버팀보(strut)의 스프링 상수(k)를 원형띠장(ring beam)의 등가 계수로 변환하여 스프링 상수(k)를 도출할 수 있다. Plane-Strain 조건 버팀보(strut)의 스프링 상수 산정은 단면적 A, 탄성계수 E, 스트럿의 간격S(1m), 스트럿의 길이 L, 그리고 스트럿에 작용하는 선 하중을 p라고 하면 스트럿의 응력은 식 (1)과 같으며, 변형률은 식 (2)와 같다. 변형률 ε가 발생했을 때, 스트럿 축 방향의 변형량 δ는 식 (3)과 같으며, 스트럿 축 방향의 스프링 상수(지반반력계수) k는 식 (4)와 같다.
| $$\sigma=\frac PA=\frac{p\cdot S}A=\frac pA$$ | (1) |
| $$\varepsilon=\frac\sigma E=\frac1E\cdot\frac pA=\frac p{E\cdot A}$$ | (2) |
| $$\delta=\varepsilon\cdot L=\frac p{E\cdot A}\cdot L=\frac{p\cdot L}{E\cdot A}$$ | (3) |
| $$k=\frac p\delta=p=\frac{E\cdot A}{p\cdot L}=\frac{E\cdot A}L$$ | (4) |
축대칭(Axial-Symmetry)조건의 원형띠장(ring beam) 스프링 상수 산정은 다음과 같다. 단면적 A, 탄성계수 E, 원형띠장의 직경 D, 그리고 원환에 작용하는 선 하중 p라고 하면 원환 응력은 식 (5)와 같으며, 변형률은 식 (6)과 같다. Plane-Strain 조건 버팀보(strut)와 동일한 변형률 ε가 발생하였다고 하면, 직경방향의 변형량 δ는 식 (7)과 같으며, 직경방향의 스프링 상수(지반반력계수) k는 식 (8)과 같다.
| $$\sigma=\frac{p\cdot D}A$$ | (5) |
| $$\varepsilon=\frac\sigma E=\frac1E\cdot\frac{p\cdot D}A$$ | (6) |
| $$\delta=\varepsilon\cdot D=\frac{p\cdot D}{E\cdot A}\cdot D=\frac{p\cdot D^2}{E\cdot A}$$ | (7) |
| $$k=\frac p\delta=p\cdot\frac{E\cdot A}{p\cdot D^2}=\frac{E\cdot A}{D^2}$$ | (8) |
Plane-Strain 조건 버팀보(strut)의 스프링상수(식 (4))와 축대칭(Axial-Symmetry)조건의 원형띠장(ring beam) 스프링 상수(식 (8))로 부터 등가 스프링 상수(지반반력계수)를 갖기 위해 지간에 대한 개념으로 Plane-Strain 조건 버팀보(strut)의 지간 길이(L)이 축대칭(Axial-Symmetry)조건의 원형띠장(ring beam)의 지간(D2)으로 간주하여 가물막이 탄소성해석시 관용적으로 적용하고 있다.
2.3 반단면 변위 검토(Axial-Symmetry)를 이용한 원형가물막이의 탄소성 해석 적용
본 연구에서는 2.2절에서 밝힌 응력-변형률의 관계를 통한 상관 관계식이 아니라 보다 합리적인 구조 검토 수행을 위하여 Fig. 3과 같이 2차원 유한요소해석을 통한 Axial-Symmetry 조건의 반단면 변위 검토 수행하여 탄소성 해석에 지반반력계수(k)를 적용하도록 하였다. 즉, 절점에 단위 하중을 적용하여 원형띠장(ring beam)의 발생 변위 값(δ)을 산출하고, 하중과 변위 값을 통하여 지반반력계수(스프링상수, k=p/δ)를 도출한 뒤 탄소성 해석에 적용하여 관용적인 방법에 의한 탄소성해석의 결과를 비교하였다.
해석에 적용된 검토조건은 새만금 내항의 특정 지역의 지반조사 결과에서 도출된 강도정수(Table 1)를 적용하였다. 지층조건은 지표면 위 5m 수위가 존재하며, 사질토(5m), 점토(13m), 그리고 자갈층 순으로 분포하며 지층근입 10m 조건을 가정하여 검토하였다. 강재는 SS400 강재로 수직벽체 두께 25mm의 단일강관을 조건을 적용, 원형보강재(ring beam, 두께 16mm, 폭 20cm)를 보강하는 조건으로 검토하였다. 강재 제원은 Table 2와 같다. 단면 형상은 원형가물막이 형태의 직경 10m, 수평보강재 수평간격 3m 조건을 적용하여 해석을 수행하였다.
Table 1. Soil properties
Table 2. Material properties of steel (SS400)
| Division |
Unit weight γ (kN/m3) |
Thickness (mm) |
Young's modulus E (kPa) |
Poison's ratio ν |
| Wall | 78.64 | 25.0 | 2.1×108 | 0.3 |
| Ring beam | 78.64 | 16.0 (width=200.0) | 2.1×108 | 0.3 |
반단면 변위 검토(Axial-Symmetry)의 유한요소해석에서 두 절점 중 한 곳은 변위 및 회전에 대해 모두 구속(Tx, Ty, Tz, Rx, Ry, Rz)을 하였고, 다른 한 절점은 Ty, Tz, Ry를 구속하여 원형보강재의 지반반력계수(스프링 상수, k)를 산출(Fig. 3)하였다. 지반반력계수(k)는 5,000.9N/mm(k=P/δ=1,000N/0.199mm)으로 탄소성 해석에 적용된 지간은 관용적 방법(L=D2)에 의해 도출한 지간의 길이는 100.0m이며, 반단면 검토에 의해 도출된 지간 길이는 L=67.2m를 적용하여 가물막이 탄소성 해석에 적용하였다.
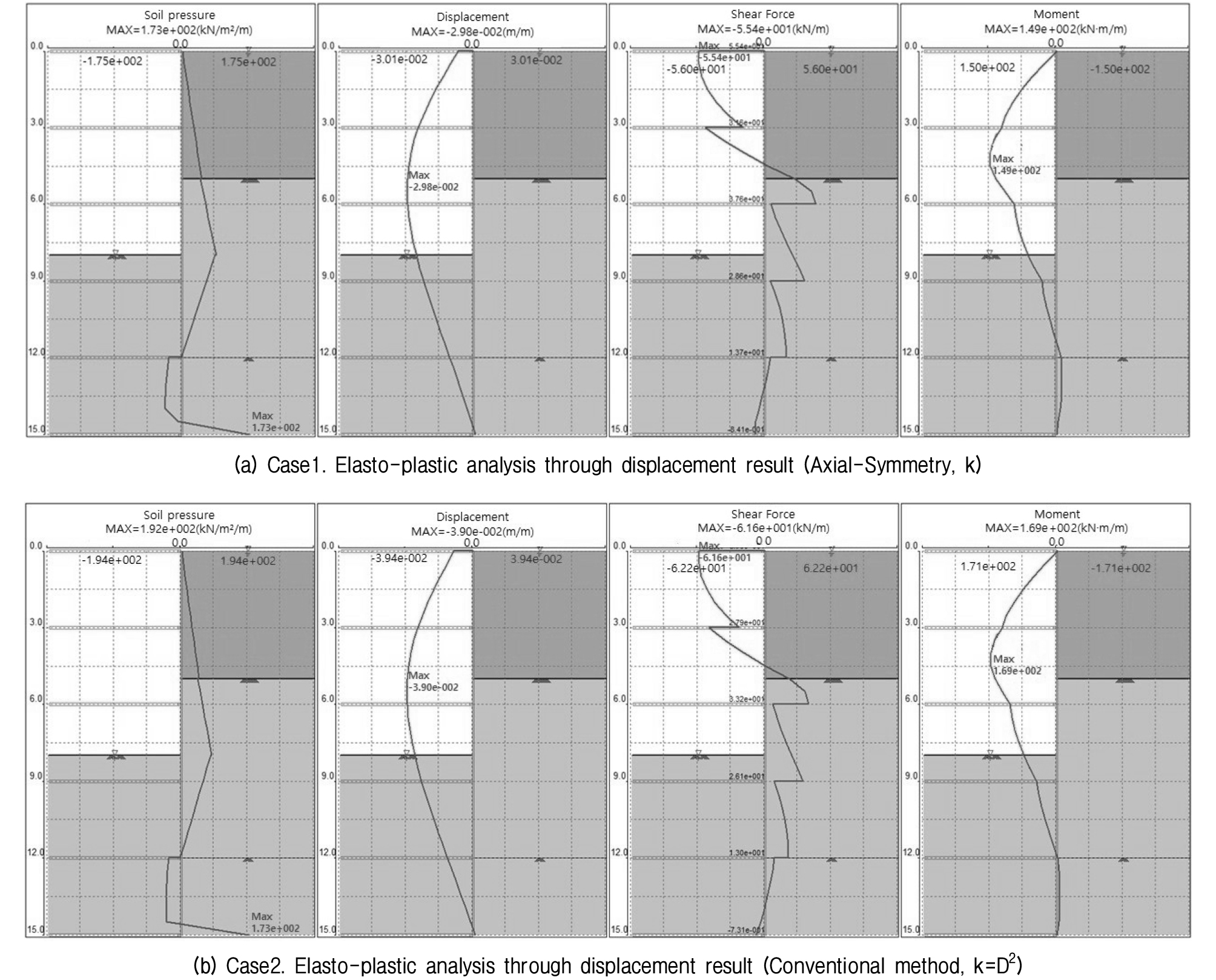
관용적인 방법과 반단면 변위 검토(Axial-Symmetry) 조건으로 도출한 값을 적용하여, Midas XD를 이용한 탄소성해석을 한 결과는 Fig. 4 및 Table 3과 같다. 반단면 변위 검토(Axial-Symmetry) 해석을 통해 지반반력계수를 산정한 방법이 기존 관용적으로 적용하던 방법보다 탄소성해석 결과 발생변위는 약 24%, 전단력은 10%, 그리고 휨응력은 12% 정도 적게 발생하는 것으로 검토되었다.
Table 3. Result of Elasto-plastic analysis (Midas XD)
3. 3차원 유한요소해석을 통한 형상 및 크기에 따른 가물막이 단면 특성 검토
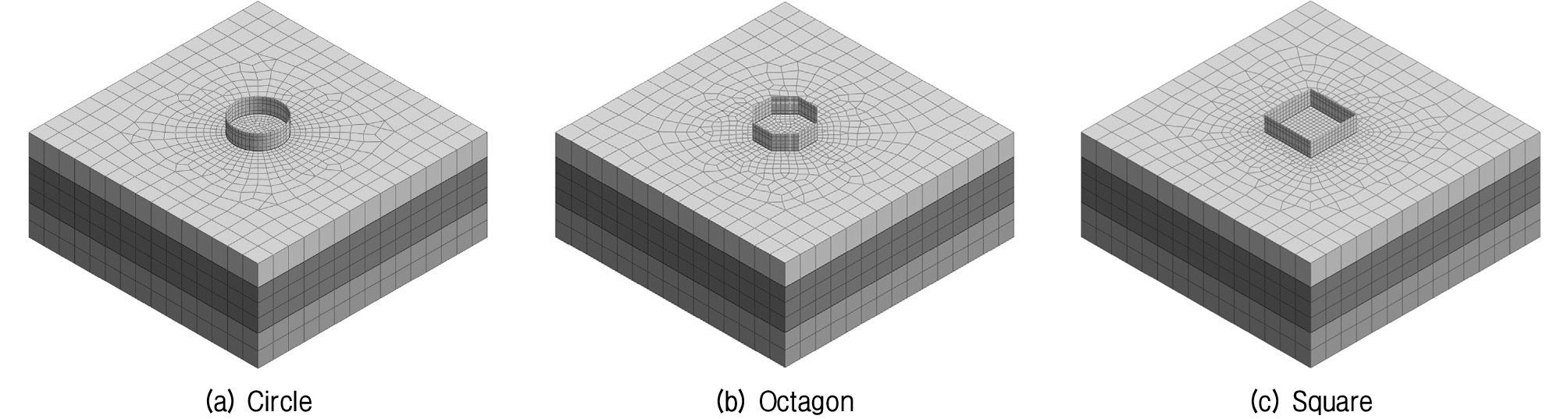
3차원 유한요소 해석의 지반 및 강재 조건은 탄소성 해석과 동일하며, 단면 형상은 원형, 팔각형, 그리고 정사각형으로 직경은 5, 10, 15m로 구분(Fig. 5)하여 검토하였다. 원형가물막이의 보강재(ring beam)는 두께(t) 16mm, 폭(width) 20cm 적용으로 가정하였다.
3.1 유한요소법의 3차원 해석 효과
최근 하드웨어 및 소프트웨어의 발달로 인하여 수치해석방법이 간편화됨에 따라 3차원 수치해석방법을 이용한 지반-구조물 거동분석에 관한 연구가 급격히 증가하고 있으며, 이에 따라 해석대상 지반 및 구조물과 인접 구조물 등의 전체 안정성을 평가함과 함께 각각의 구성부재의 변형 및 부재력을 보다 간편하게 검토할 수 있게 되었다. 대표구간을 평면 변형률 조건으로 모델화하여 해석하는 2차원 수치해석방법은 지층의 변화, 흙막이 벽체 및 지지구조를 표준화하여 해석하므로 전체 구성 부재의 각각에 대한 부재력이 정확하게 산출되지 못하며, 대표구간의 산출값으로만 흙막이 벽체를 설계하게 된다. 특히 폐합단면 구조의 흙막이 구조에서 벽체의 모서리 구간과 중앙부의 변위 및 지반변형에는 큰차이가 있으며, 이에 따라 평면 변형률 조건의 2차원 수치해석을 통한 흙막이 벽체의 변위 및 지반변형은 3차원 해석결과와 비교하여 크게 나타나고 있다(Bono et al., 1992; Ou et al., 1996; Lee et al., 1998; Finno et al., 2007). 이와 같은 2차원 수치해석 결과를 이용한 흙막이 구조물의 설계는 비경제적인 과다설계의 원인일 될 수 있다.
따라서, 본 연구에서는 대형 가물막이의 단면 형상과 크기에 따른 구조적 특성을 파악하고자 하였다.
3.2 유한요소해석 모델링 및 검토 결과
본 검토에서 유한요소해석(FEM) 프로그램인 Midas GTS NX를 이용하여 3차원 해석을 수행하였으며, 모델링 단면은 Fig. 6과 같다.
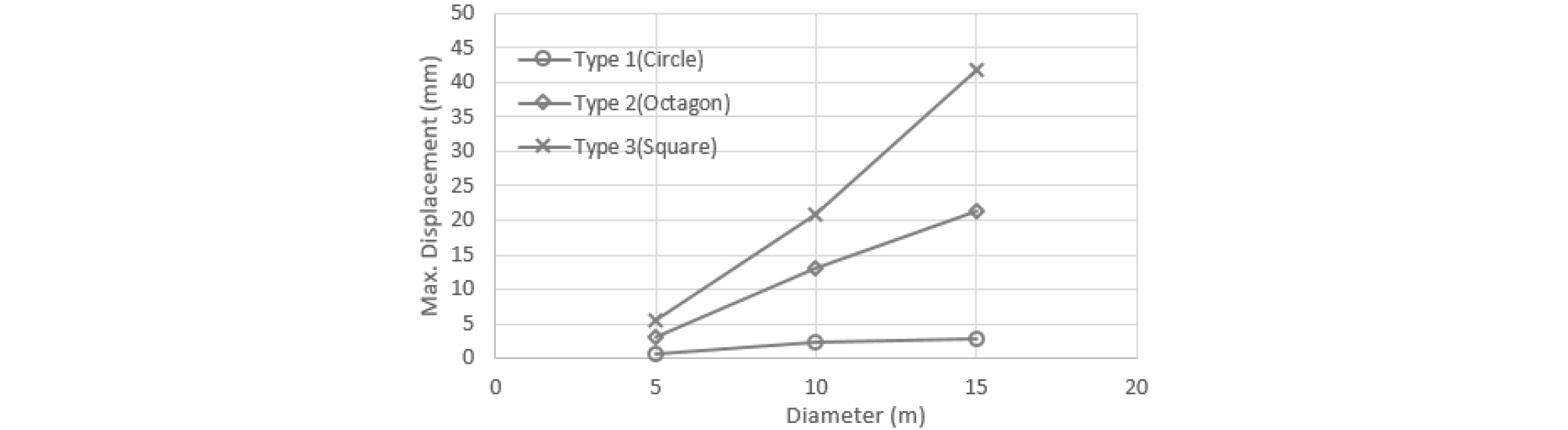
형상 및 크기에 따른 조건별 최대발생 변위 검토 결과는 Table 4 및 Fig. 7~8과 같다. 원형의 형상에서 발생 변위가 크기별로 가장 작게 발생되었으며, 구조물의 단면 크기가 커질수록(D=5m에서 10m, D=10m에서 15m 증가 시) 단면 형상별 발생 변위는 원형 타입의 변위 증가량 67%, 20%, 팔각형 타입 76%, 40%, 그리고 정사각형 타입 75%, 50%으로 증가하는 것으로 검토되었다. 2차원 반단면 변위 검토를 통한 탄소성 해석시 최대 발생변위는 29.8mm로 3차원 유한요소해석 결과 2.24mm보다 10배 이상 차이가 나는 것으로 검토(Table 3과 Table 4 참조)되었다.
Table 4. Result of displacement by case
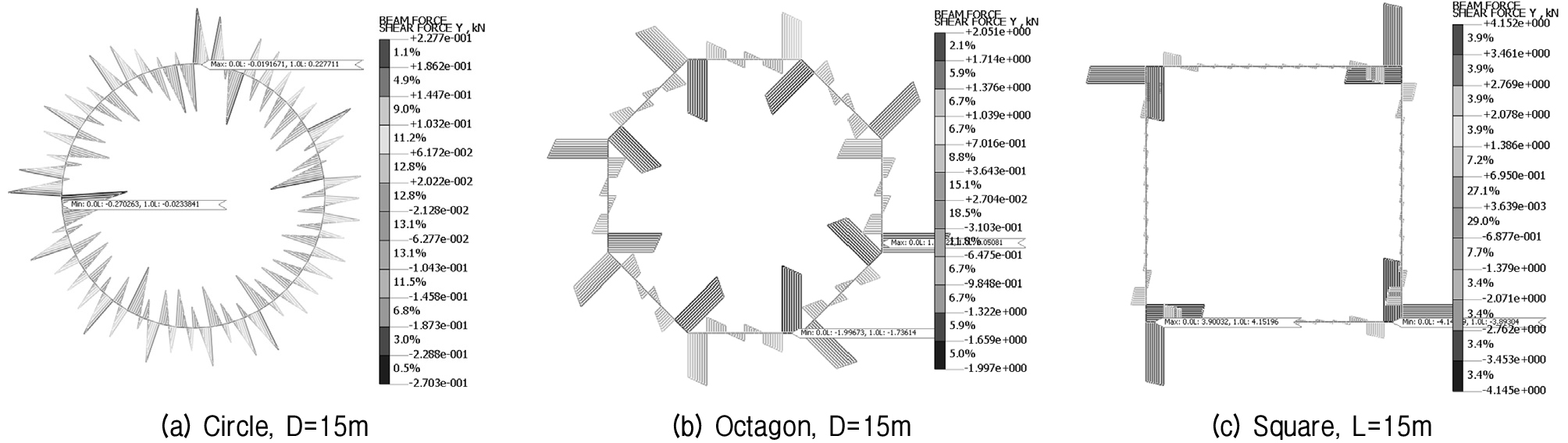
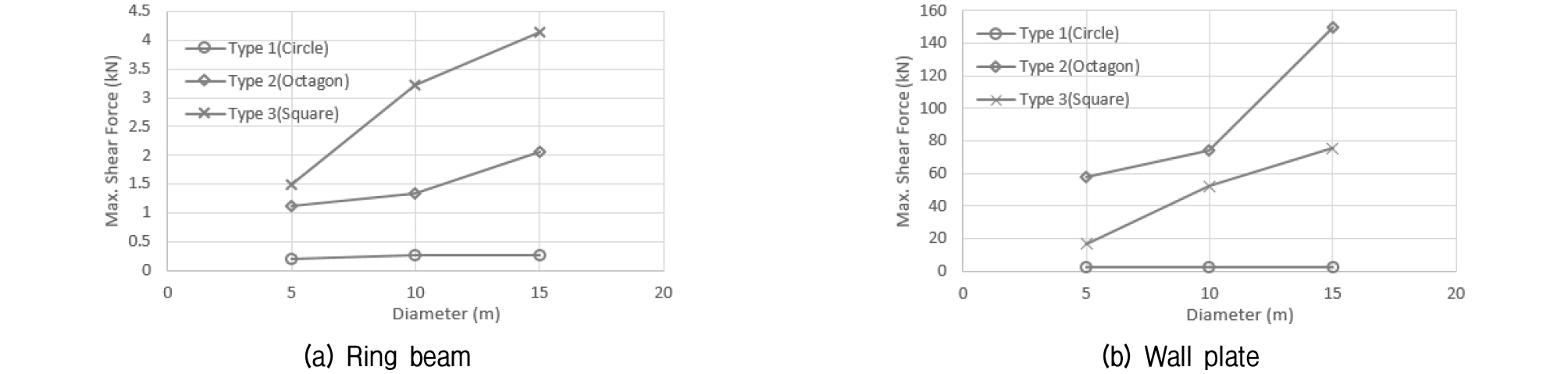
조건별 발생 전단력은 Table 5 및 Fig. 9~10과 같다. 전단력의 경우 수직 3m 간격으로 설치된 수평보강재가 받는 전단력보다 강관벽체가 받는 전단력이 지배적으로 큰 것으로 검토되었으며, 변위 검토 결과와 동일하게 원형구조물이 단면 크기에 관계없이 전단력을 아주 작게 받는 것으로 검토되었다.
Table 5. Result of shear force by case
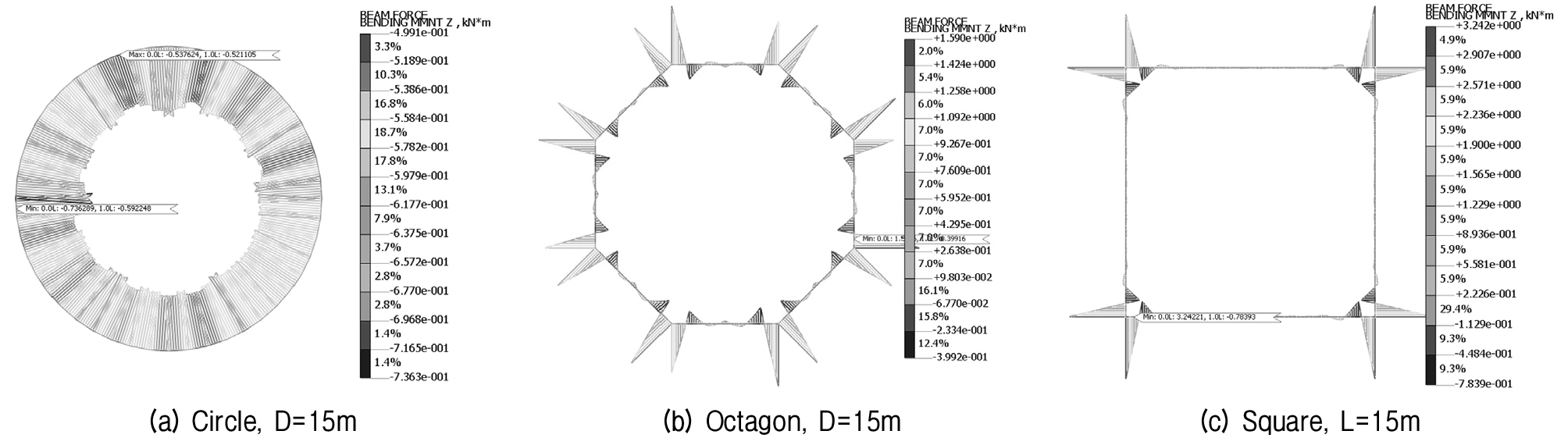
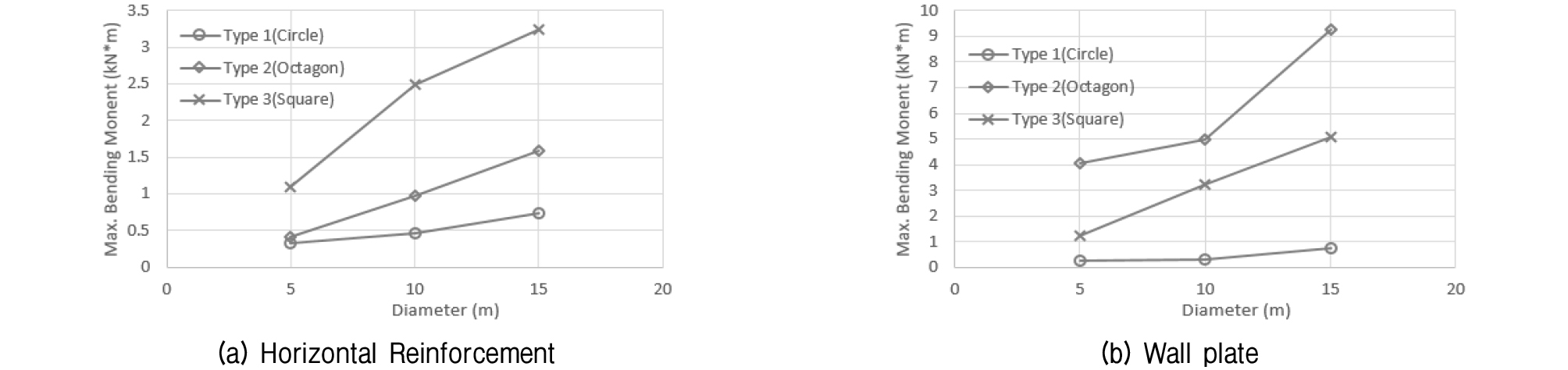
조건별 발생 휨모멘트 검토 결과는 Table 6 및 Fig. 11~12와 같다. 휨모멘트의 경우 원형 타입에서 수평보강재(Horizontal Reinforcement)가 다른 형상보다 최소 21%에서 최대 77% 작게 받는 것으로 검토되었으며, 강관벽체에서도 원형 타입에서 다른 형상보다 현저하게 작은 휨모멘트가 발생하는 것으로 검토되었다. 하지만 강관벽체 휨모멘트에서는 변위나 발생 전단력 결과와 달리 팔각형 타입이 정사각형 타입보다 발생 값이 크게 나타난 것이 차이점이었다.
Table 6. Result of bending moment by case
본 연구에서 관용적인 방법과 반단면 변위 검토(Axial-Symmetry)를 통한 2차원 탄소성 해석결과와 3차원 유한요소 해석을 통하여 구조적 특성 비교는 3차원 모델링시 셀(shell) 요소 사용으로 휨/전단과 같이 단면력 형태로 결과값을 제공하는 것이 아니기에 최대 발생변위 값은 비교가 가능(3차원 해석시 2.24mm, 2차원 반단면 변위 검토를 통한 해석시 29.8mm)하였으나, 발생 부재력에 대한 비교 검토는 이루어지지 않았다.
4. 결 론
본 연구에서는 원형벽체에 대한 2차원 탄소성해석 적용시 원형단면에 대한 구조적인 특성을 정확히 반영하지 못하여 구조단면에 대한 검토 결과가 과대하게 산출되는 점을 보완하기 위하여 원형단면에 대해 탄소성해석시 기존에 관용적으로 검토해왔던 방법과 2차원 유한요소해석을 통한 반단면 변위검토(Axial-Symmetry) 조건을 적용하여 지반반력계수(스프링상수, k)를 산정하여 탄소성 해석에 적용하여 검토 결과를 비교하였다.
더불어 3차원 유한요소해석(FEM)을 통하여 대형 가물막이의 단면 형상과 크기에 따른 전단력, 휨모멘트, 그리고 발생변위를 확인하여 그 특성을 비교분석 하였다.
(1) 원형가물막이에 대한 탄소성 해석시 원형보강재(ring beam)에 대한 반단면 변위 검토(Axial-Symmetry)를 통하여 지반반력계수(스프링상수, k)를 도출하여 적용한 해석 결과가 기존에 일반적으로 사용해온 관용적 검토 방법보다 발생변위는 약 24%, 전단력은 10%, 그리고 휨응력은 12% 정도 적게 발생하는 것으로 검토되었다. 원형가물막이에 대한 경제적인 설계를 위하여서는 탄소성해석 적용시 반단면 변위 검토(Axial-Symmetry)를 이용한 2D 유한요소해석을 병행한 탄소성해석이 필요할 것으로 판단된다.
(2) 단일강관 가물막이에 대한 단면의 형상 및 크기에 따른 3차원 유한요소 해석 결과 가물막이의 구조 특성은 다음과 같다.
① 발생 변위 검토 결과 원형의 형상에서 발생 변위가 크기별로 가장 작게 발생되었으며, 단면 직경이 커질수록 발생변위는 크기 증가에 따른 원형(직경 5m와 직경 10m 변위 증가량 67%, 직경 10m와 직경 15m 변위 증가량 20%)보다 증가폭이 단면 크기 증가별로 팔각형 타입(직경 5m와 직경 10m 변위 증가량 76%, 40%), 정사각형 타입(직경 5m와 직경 10m 변위 증가량 75%, 50%)에서 크게 증가하는 것으로 검토되었다.
② 조건별 발생 전단력은 수직 3m 간격으로 설치된 수평보강재가 받는 전단력보다 강관벽체가 받는 전단력이 지배적으로 큰 것으로 검토되었으며, 변위 검토 결과와 동일하게 원형 형상의 구조물이 크기에 관계없이 전단력이 아주 작게 발생하는 것으로 검토되었다.
③ 휨모멘트의 경우 원형 타입에서 수평보강재가 팔각형이나 정사각형 형상보다 최소 21%에서 최대 77% 작게 받는 것으로 검토되었으며, 강관벽체에서도 원형 타입에서 다른 형상보다 현저하게 작은 휨모멘트가 발생하는 것으로 검토되었다.
(3) 3차원 유한요소해석을 통한 가물막이의 형상과 크기에 따른 구조적 특성을 비교검토한 결과 원형단면이 발생변위나 부재력에서 효과적인 것으로 검토되었다. 즉, 현장에서 가물막이 적용시 시공성과 경제성만 확보된다면 원형가물막이 형태의 단면 적용으로 구조적인 안정성을 보다 효과적으로 확보할 수 있을 것으로 판단된다.