1. 서 론

일반적으로 Back-to-Back 보강토옹벽(이하 BTB 보강토옹벽이라 칭함)은 고속도로 램프구간, 교량 교대부, 계곡 횡단도로, 경사로 진입도로 그리고 제방 및 소음방벽, 낙석방지 시스템 등 여러 가지 목적으로 적용되고 있지만, 그 축조의 한계로 인해 대부분 토목섬유 보강재를 이용한 보강토옹벽 형식으로 사용되고 있다. BTB 보강토옹벽에 대해 국내의 경우 특별한 규정이나 설계기준이 없으며 미국 FHWA 설계기준(Ryan et al., 2009)에 개략적으로 서술되어 있긴 하나 중첩에 따른 활동 메커니즘에 대해 이론화된 것이 없어 정형화된 설계가 어려운 실정이다.

국·내외 연구동향을 살펴보면 모형토조를 사용한 축소모형실험(Kim et al., 2008), 유한요소해석에 의한 거동 메커니즘 분석(Mohamed et al., 2016) 또는 불연속체해석으로 거동 특성(Yoo et al., 2011)을 연구한 것이 대부분으로 이러한 접근법은 토목섬유 보강재의 마찰력 및 크리프 감소계수RF_CR, 내구성 감소계수RF_D, 시공성 감소계수RF_ID 등이 반영된 장기설계인장강도를 고려할 수 없기 때문에 실제 설계단계에서 적용하기 어려운 문제가 있다. 따라서 본 연구에서는 실제 설계단계에서 사용하고 있는 토목섬유 보강재의 장기설계인장강도를 반영한 BTB 보강토옹벽의 옹벽폭비 변화(옹벽폭비, W_b/H)에 따른 안정성을 분석하여 거동 특성 및 높이에 따른 최적 보강재길이(보강길이비, L/H)에 대해 고찰해 보았다.

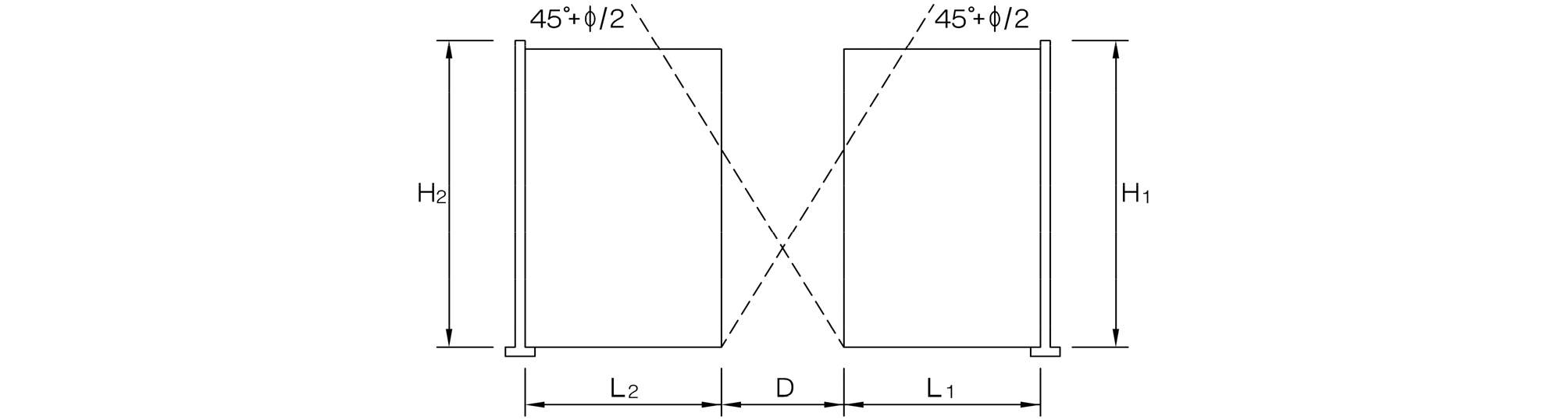
우선 FHWA 설계기준을 살펴보면 크게 두 가지 Case로 기술되어 있다(FHWA, 1997). 여기서 Case I은 양립하는 두 옹벽의 보강재가 겹치지 않고 떨어져 있는 경우로 두 옹벽 사이의 거리(D)가 D = H₁tan(45°-φ°/2) 보다 짧아 옹벽높이(H₁)가 평행 상태에 있는 옹벽보다 더 크면 활동 파괴선이 보강재를 통과하여 인장력을 감소시킨다. 그러나 좌우 옹벽이 충분히 이격되어 있다면 상호 응력의 간섭이 없어 각각의 옹벽은 독립적으로 거동하게 된다. 이때 이격거리가 아래 식 (1)의 조건일 때 양립하는 두 옹벽은 각각 독립체로 간주하여 설계할 수 있다.

Fig. 1

Case I Back-to-Back MSE walls (FHWA, 1997)

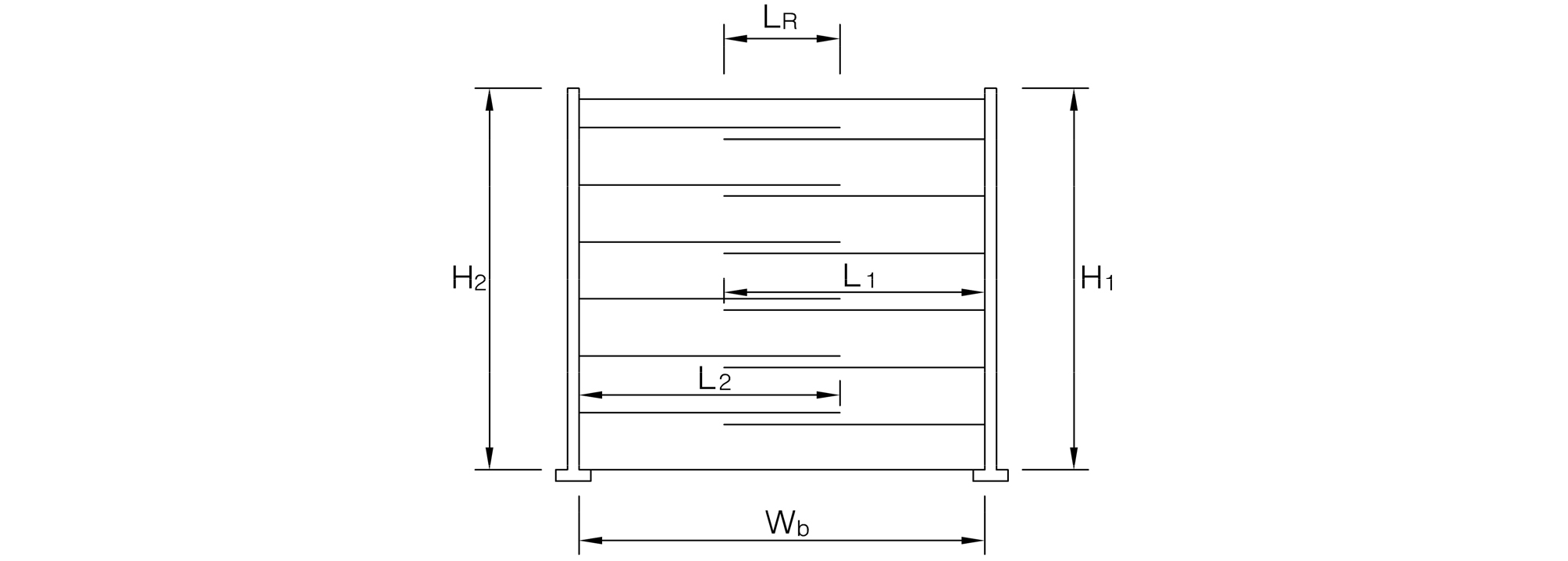
반면 Case II는 양립하는 두 옹벽이 보강재가 겹치는 경우로 이때 보강재가 서로 중첩되는 구간의 길이(L_R)가 0.3H₂보다 커 H₂가 평행 상태에 있는 옹벽보다 짧으면 옹벽의 구조는 독립적인 구조체로 해석되나 뒤채움토에 의한 주동토압은 고려하지 않아도 된다.

또한, FHWA 설계기준에서는 보강재가 서로 중첩되는 구간의 길이가 0.3H₂보다 큰 Case II의 경우 보강길이비가 0.6보다 같거나 크게 하여야 하며 옹벽 높이에 따른 양립하는 옹벽폭비(W_b/H₁)는 1.1과 같거나 크게 설계하도록 권고하고 있다. 이때 최소 보강길이비가 0.6일 때 보강재가 중첩되지 않는 조건이면 옹벽폭비는 1.2가 되며, 양립하는 옹벽폭비가 최소 1.1 조건에서 보강재가 중첩되지 않는다면 보강길이비는 0.55가 된다. 두 조건을 만족시킬 때 최소 보강재의 중첩길이는 L/H=0.05가 되므로 FHWA 설계기준에 따르면 실제 BTB 보강토옹벽은 보강재가 거의 중첩되지 않게 설계되어야 한다.

Fig. 2

Case II Back-to-Back MSE walls (FHWA, 1997)

일반적으로 BTB 보강토옹벽은 좌우측에 대칭하여 축조되므로 단일 보강재 레이어를 사용하면 보강재가 서로 충첩되지 않아 효율적인 대안으로 보이나 이 대안은 수평변위가 발생하지 않아 옹벽의 상단에서 하단으로 정지토압(K_o) 상태를 생성하여 독립적인 보강토옹벽 설계보다 더 높은 인장력이 요구된다. 본 연구에서는 이러한 BTB 보강토옹벽의 특성을 고려하여 양립하는 옹벽의 높이 변화와 옹벽간의 폭비에 따른 안전율을 도출하고 각각의 조건에서 높이에 따른 보강재 길이의 비(L/H)에 따른 안전율 변화를 분석하여 보강재 겹침에 따른 상호작용, 옹벽높이 및 옹벽폭비에 따른 최적 보강길이비를 산정하였다.

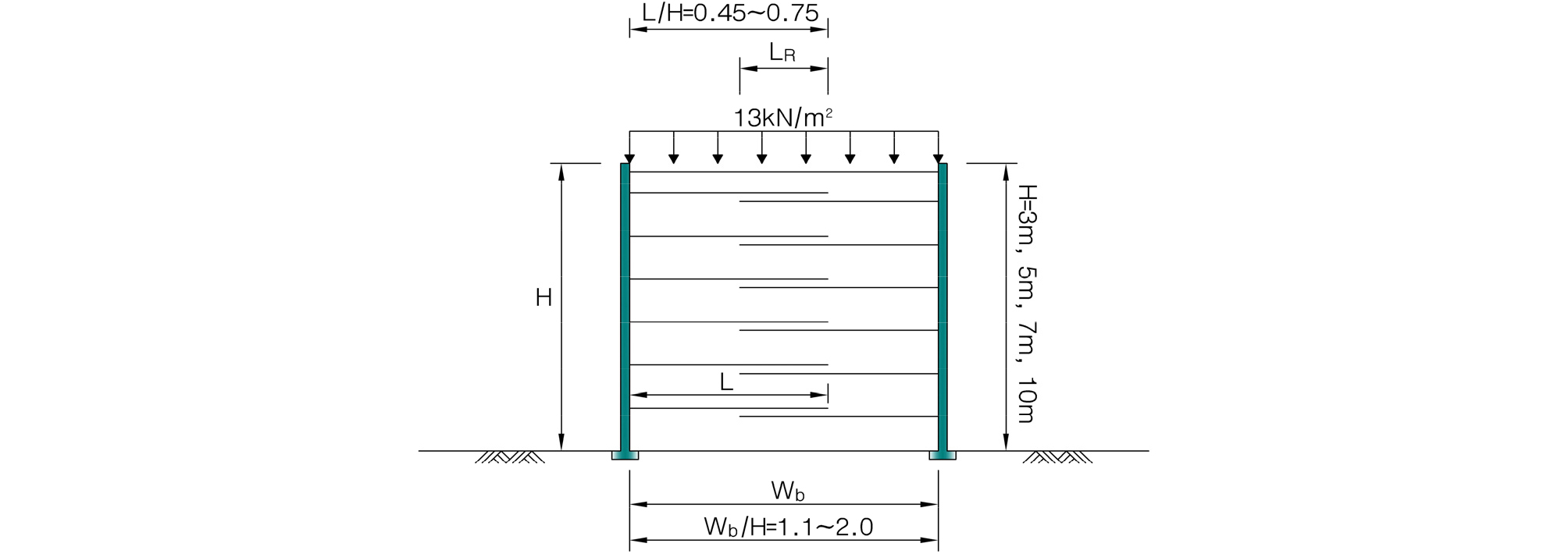
FHWA 설계기준을 토대로 BTB 보강토옹벽 높이를 일반적으로 가장 많이 적용되고 있는 3.0m, 5.0m, 7.0m, 10.0m 총 4단계, φ° = 30°로 가정하고 양립하는 옹벽간의 상호 응력 간섭이 발생하는 조건은 1.1H < W_b < 1.77H 범위의 D ≤ H × tan(45°-φ°/2)를 대상으로 옹벽간의 폭비는 1.1H, 1.4H, 1.7H, 2.0H 총 4단계로 설정하였다. 가정한 조건에서 인장강도 60, 80, 100, 150kN/m²의 토목섬유 보강재를 사용하여 높이별 최적단면(표준단면)을 설정하고 이를 토대로 각 단면에 대해서 보강길이비에 따른 안전율 변화를 관찰하였다.

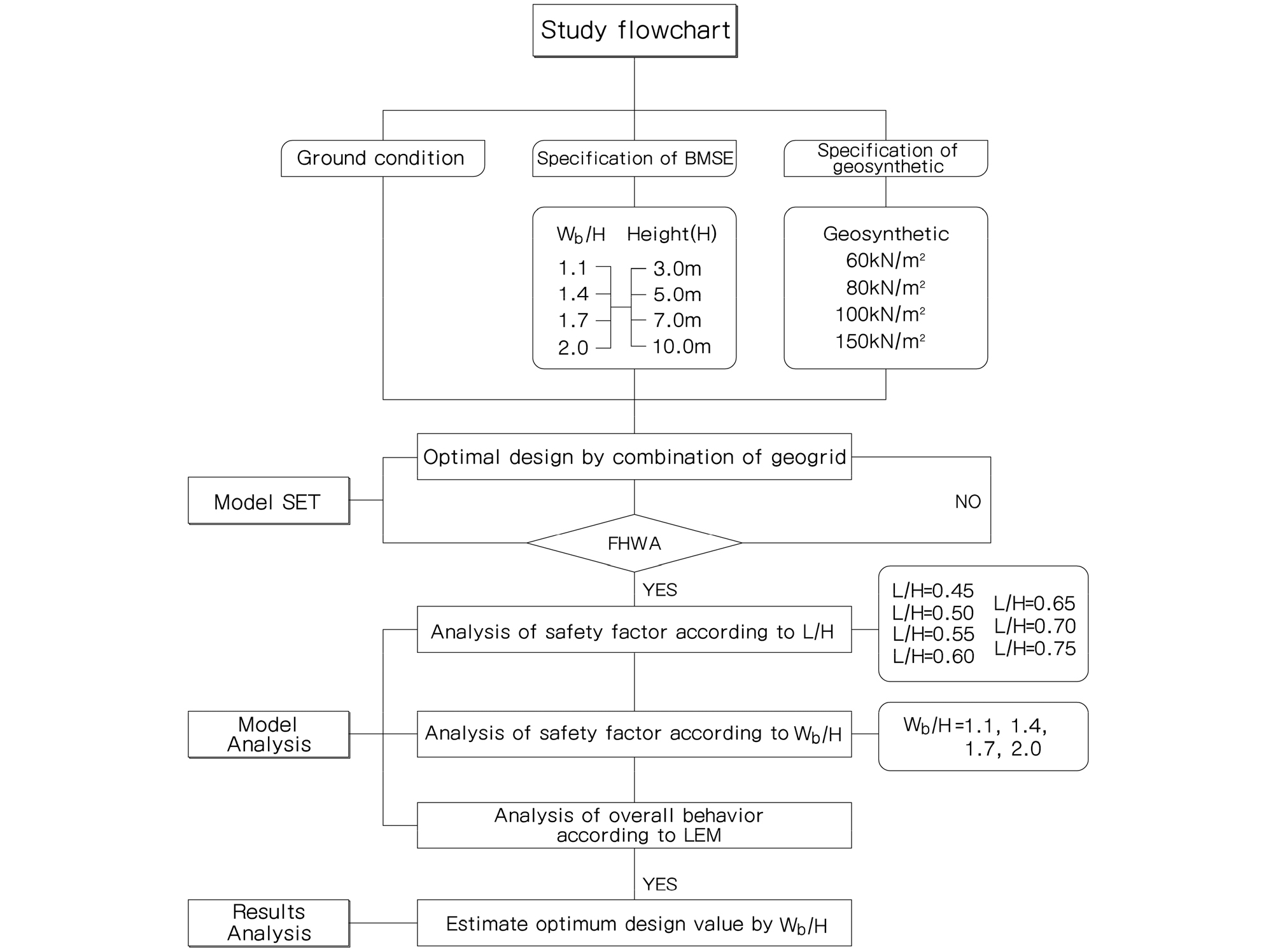
각 단계별 최적의 보강재 길이를 도출하기 위해 높이별 보강길이비는 0.45, 0.50, 0.55, 0.60, 0.65, 0.70, 0.75(총 7단계), 상재하중 조건은 BTB보강토옹벽이 주로 고속도로 램프구간에 적용되는 것을 고려하여 13kN/m²로 하였으며 폭 대 높이비에 따른 높이별 설정단면은 Fig. 3, 연구 흐름도는 Fig. 4와 같다.

Fig. 3

Condition of analysis section at W_b/H=1.1

Fig. 4

Study flowchart

2. BTB 보강토옹벽의 최적보강길이비 산정

2.1 FHWA 설계기준에 따른 W_b/H 고찰

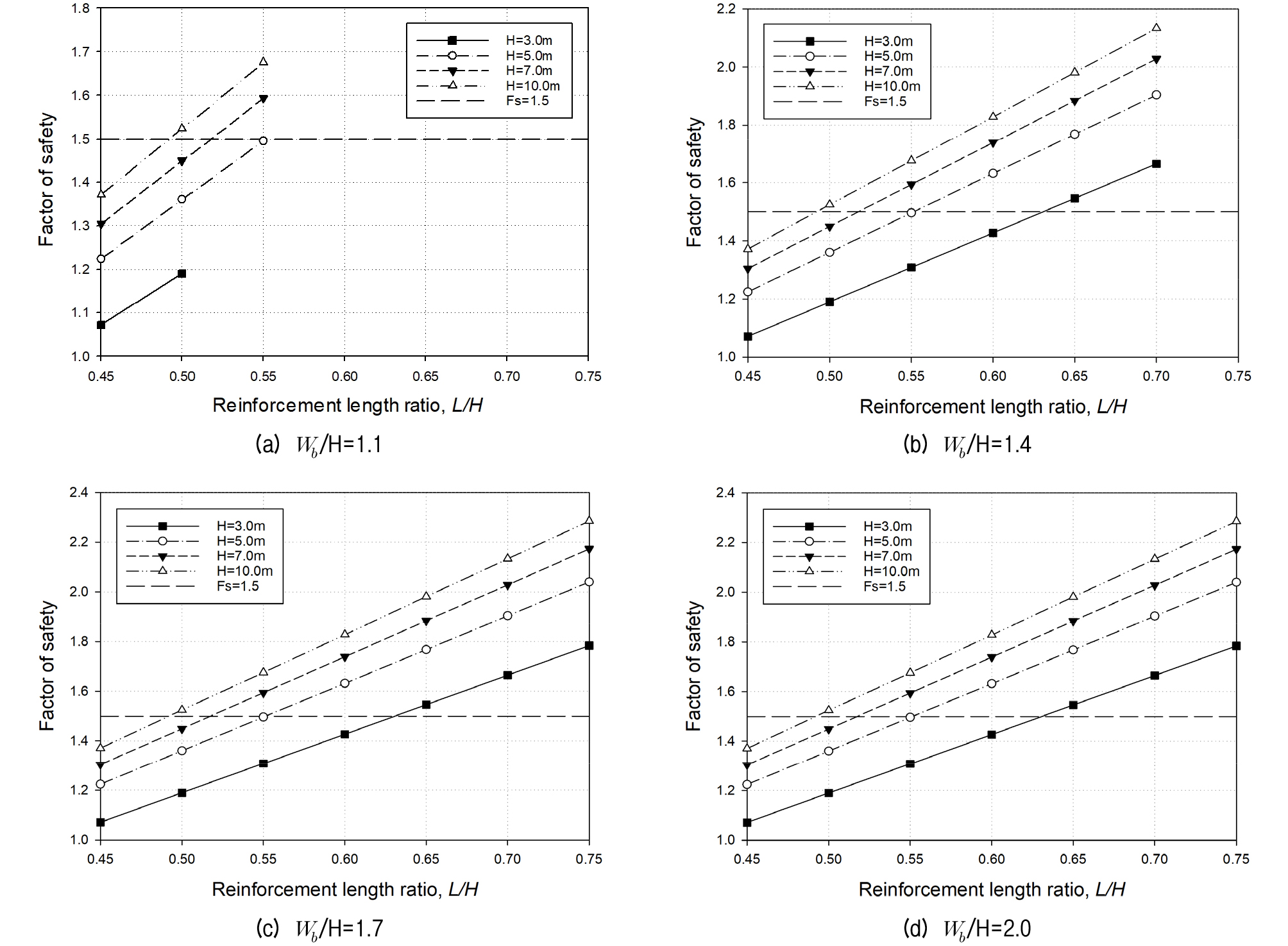
우선, FHWA 설계기준을 준용한 타이백(tie-back) 수치해석은 MSEW(ADAMA Eng, 2008)를 사용하였으며 이를 통해 옹벽간의 폭 대 높이비에 대해 고찰한 결과, W_b/H=1.1∼2.0 모두 옹벽높이 3.0∼10.0m까지 보강길이비가 증가할수록 안전율이 매우 선형적으로 증가하며 옹벽의 높이가 높을수록 안전율이 증가하는 것으로 나타났다. 각 옹벽폭비에 따른 결과를 보면, W_b/H=1.1일 때 5.0m는 보강길이비 0.60, 7.0m는 0.55, 10.0m는 0.50부터 기준안전율을 확보하여 적용이 가능한 것으로 평가되었으며 W_b/H=1.4에서는 3.0m는 0.65, 5.0m는 0.60, 7.0m는 0.55, 10.0m는 0.50부터 기준안전율을 확보하였다. 또한 W_b/H=1.1에서 0.60부터, W_b/H=1.4의 경우 0.75부터 보강길이비가 증가함에 따라 겹칩이 발생하는 구간에 대해 FHWA 설계기준을 준용한 보강토옹벽 전용프로그램이 해석적 방법을 지원하지 못하는 것으로 확인되었다.

W_b/H=1.7일 때 옹벽높이 3.0m는 보강길이비 0.65, 5.0m는 0.60, 7.0m는 0.55, 10.0m는 0.50부터 기준안전율을 확보하였으며 W_b/H=2.0의 경우 옹벽 높이 3.0m는 0.65, 5.0m는 0.65, 7.0m는 0.55, 10.0m는 0.50부터 안전율을 확보하여 적용이 가능한 것으로 평가되었다.

특히 옹벽의 높이가 높을수록 안전율이 증가하는 것은 수직응력(σ_v) 증가에 따라 보강재의 마찰력(σ_r)이 증가하면서 높아지는 것으로 이는 옹벽이 높아야 안정하다는 인식으로 이어질 수 있으므로 주의해야 할 부분이다.

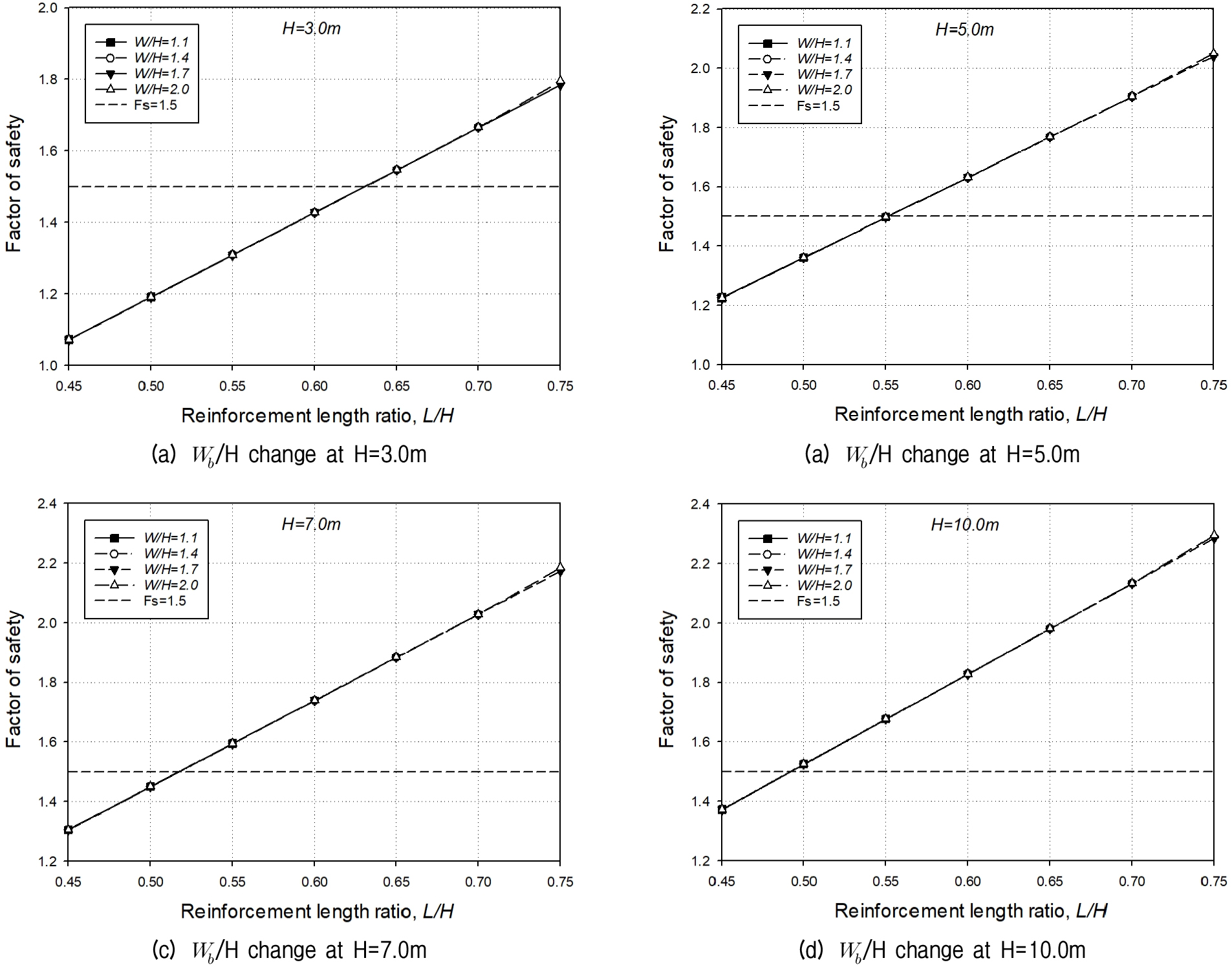
분석결과를 토대로 높이별 옹벽폭비(W_b/H) 변화를 살펴보면 Fig. 5에 나타난 것과 같이 H=3.0∼10.0m까지 모두 동일한 결과가 도출되었다. 이는 자칫 BTB 보강토옹벽이 같은 높이에서는 좌·우 옹벽의 폭과 무관하게 안전율이 동일하다는 결과로 받아들일 수 있다.

Fig. 5

Sliding safety factor by height according to L/H change

하지만 옹벽폭비의 변화에도 불구하고 안전율의 변화가 없는 것은 FHWA 설계기준이 보강재의 상호작용을 고려하지 못하고 BTB 보강토옹벽의 중심면에서 한쪽 단면만이 고려됨에 따라 양립하는 옹벽간의 이격거리는 아무런 영향을 받지 않기 때문이다. 따라서 이러한 결과를 그대로 받아들여 설계가 이루어진다면 매우 불안정한 상태를 초래하게 된다.

본 연구에서는 상기 결과를 검증하기 위해 동일한 조건에서 REWall(MIDAS, 2018)을 사용하여 수치해석을 수행하였으나 모두 동일한 결과가 도출되었다.

Fig. 6

Safety factor on W_b/H change at H=3.0~10.0m

2.2 한계평형해석에 의한 고찰

BTB 보강토옹벽는 양립하는 보강토이기 때문에 일체화된 상태에서 전체 거동이 발생할 수 있으며 보강재 중첩구간에 발생하는 응력 변화는 보강토옹벽의 안정성에 직결되는 문제이기 때문에 옹벽폭비 변화에 따른 안정성 변화는 실제 설계단계에서는 반드시 고려되어야 하나 앞서와 같이 FHWA 설계기준을 준용한 해석에서는 이를 고려하지 못하는 것으로 확인됨에 따라 본 연구에서는 중첩에 따른 안정성 변화를 분석하기 위해 동일한 조건에서 한계평형해석(LEM)을 추가로 수행하여 높이 및 옹벽폭비 변화에 따른 최적 보강길이비에 대해 고찰하였으며 수치해석은 SoilWorks(MIDAS, 2018)를 사용하였다.

(1) 보강길이비 변화에 따른 W_b/H 안전율 고찰

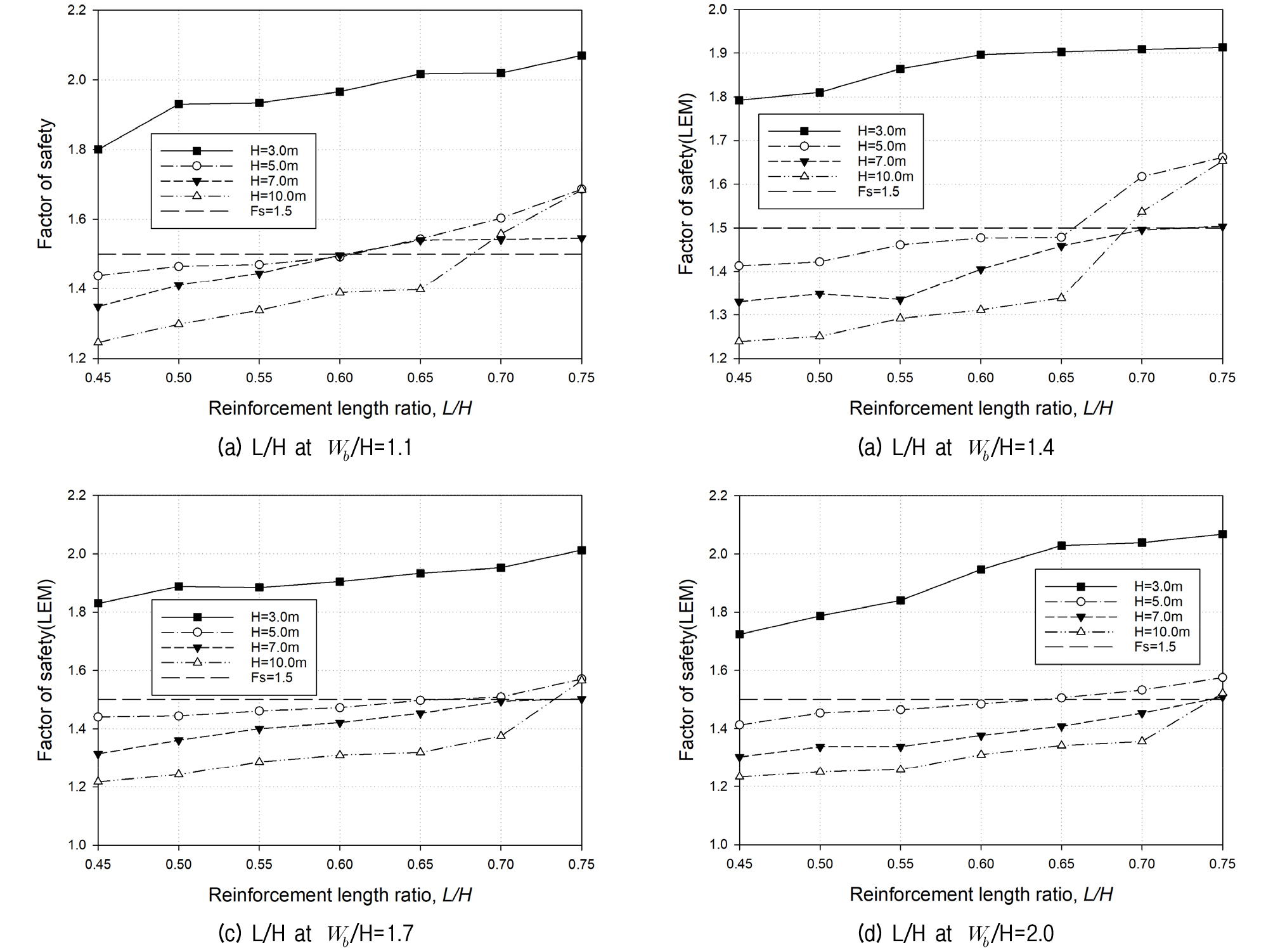
옹벽폭비가 W_b/H=1.1일 때 옹벽높이 3.0m는 보강길이비 변화에 따라 전체활동에 대한 안전율이 1.800∼2.070, 5.0m는 1.438∼1.687로 0.65부터 기준안전율을 만족하였으며 7.0m는 1.348∼1.546로 5.0m와 유사하게 0.65부터 기준안전율을 만족하였다. 10.0m의 경우 활동에 대한 안전율이 1.246∼2.866으로 도출되었으나 특이하게 0.70부터 파괴형태가 좌우로 양립하는 보강토옹벽 전체가 활동영역에 포함되는 양상이 되어 비이상적으로 평가되었다.

W_b/H=1.4에서는 옹벽높이 3.0m는 보강길이비 0.45∼0.75에서 1.792∼1.914, 5.0m는 1.413∼1.662로 0.70부터 기준안전율을 만족하였다. 7.0m는 1.330∼1.503로 5.0m보다 다소 불리하게 0.75부터 기준안전율을 만족하였으며 10.0m의 경우 활동에 대한 안전율이 1.239∼3.568로 평가되었으나 0.70부터 안전율이 다소 비이상적으로 상승하였다.

W_b/H=1.7의 경우 옹벽높이 3.0m는 보강길이비 0.45∼0.75에서 1.830∼2.012로 기준안전율을 모두 확보하였으며 5.0m는 1.440∼1.571로 0.70부터 기준안전율을 만족하였다. 7.0m는 1.314∼1.502로 0.75부터 기준안전율을 만족하였으며 10.0m의 경우 1.217∼3.013로 보강토옹벽 전체가 활동영역에 포함되면서 0.75부터 안전율이 가파르게 상승하였다.

W_b/H=2.0에서 옹벽높이 3.0m는 보강길이비 0.45∼0.75에서 1.724∼2.068로 기준안전율을 모두 확보하며 5.0m는 1.412∼1.576로 0.65부터 기준안전율을 만족하였다. 7.0m는 1.302∼1.509로 0.75부터 기준안전율을 만족하였으며 10.0m의 경우 1.232∼2.669로 0.75부터 앞서와 마찬가지로 안전율이 가파르게 상승하였다.

해석결과를 종합해 보면, 보강길이비가 증가하면서 안전율도 소폭으로 증가하나 FHWA 기준과 달리 옹벽의 높이가 높아질수록 안전율이 감소하였다. 즉, 타이백(tie-back) 해석방법이 옹벽의 높이가 높아질수록 수직응력(σ_v) 증가로 보강재의 마찰력(σ_r)이 증가하면서 안전율이 높아지는 것에 반해 한계평형해석은 옹벽의 높이가 높아질수록 활동토체가 커지면서 안전율이 낮아지는 것으로 분석된다. 양립하는 BTB 보강토옹벽을 일체화된 하나의 구조물로 간주할 때 구조물의 높이가 높아질수록 불안정해지는 것이 더 상식적인 결과로 보이며 이는 실제 설계단계에서 충분히 고려되어야 할 부분이다.

Fig. 7

Change in safety factor according to L/H

(2) 높이별 W_b/H 변화에 따른 안전율

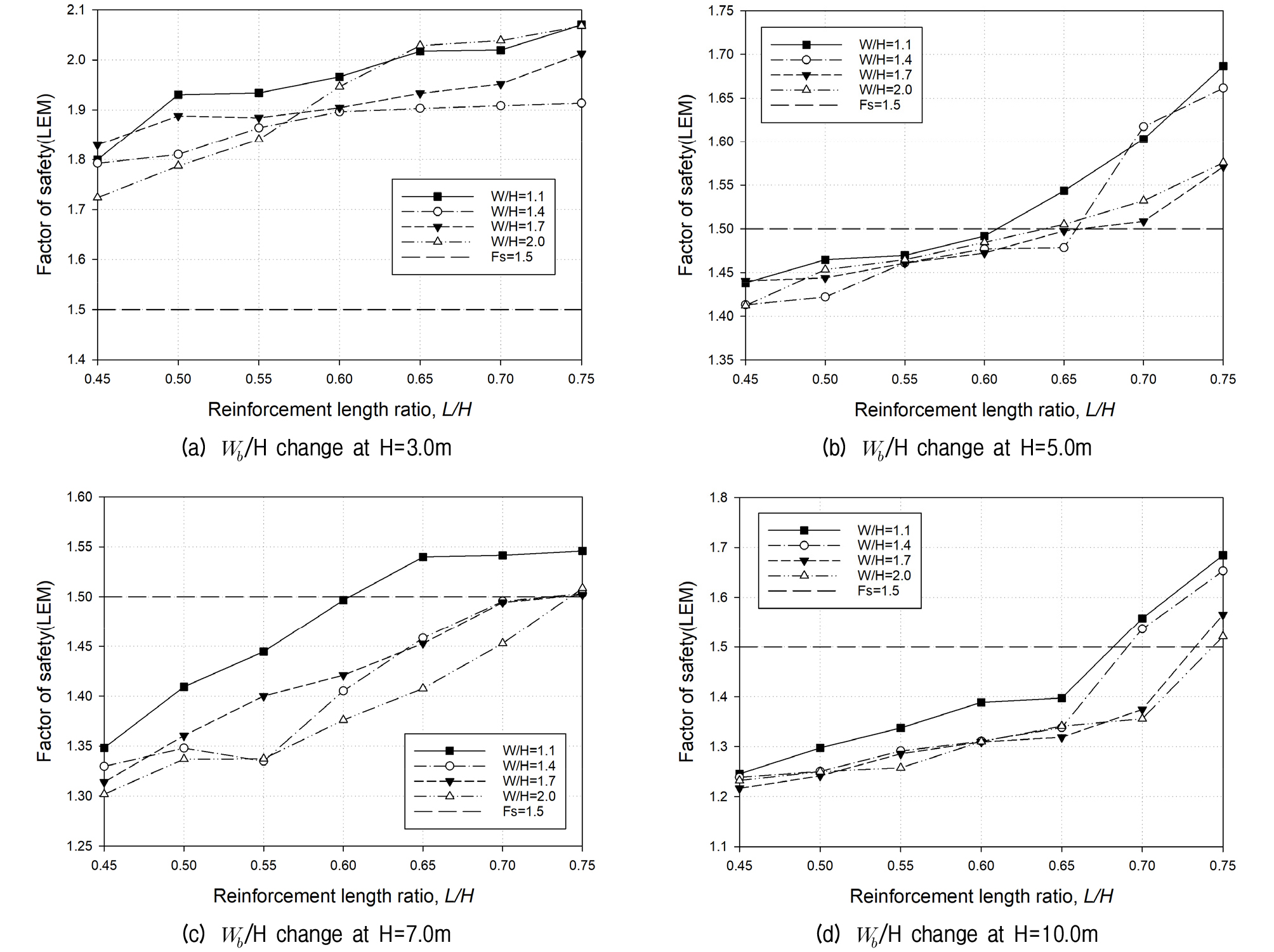
우선 옹벽높이 3.0m는 W_b/H=1.1∼2.0 전부 보강길이비 0.45∼0.75에서 전체활동에 대한 안전율이 1.724∼2.070로 기준안전율을 모두 확보하였다. 5.0m의 경우 W_b/H=1.1은 1.438∼1.687로 보강길이비가 0.65부터 기준안전율을 만족하며 W_b/H=1.4∼1.7은 1.413∼1.662로 보강길이비 0.70, W_b/H=2.0은 1.412∼1.576으로 보강길이비 0.65부터 안정한 것으로 나타났다.

옹벽높이 7.0m에서는 W_b/H=1.1은 활동에 대한 안전율이 1.348∼1.546로 보강길이비 0.65부터 안정성을 확보하며 W_b/H=1.4∼1.7은 1.302∼1.509로 0.75부터 안정한 것으로 평가되었다.

또한, 옹벽높이 10.0m의 경우 W_b/H=1.1∼2.0은 활동에 대한 안전율이 1.217∼3.568로 보강길이비 0.70부터 안정성을 확보하나 0.70부터 안전율이 급격히 상승하는 경향을 보인다. 이는 좌우로 양립하는 보강토옹벽 전체가 활동영역에 포함되는 문제로 분석되며 이러한 결과로 볼 때 10.0m의 경우 W_b/H=2.0 이내에서는 다소 불안정한 것으로 판단되므로 실제 설계단계에서는 매우 신중한 접근이 필요하다. FHWA 설계기준 해석과 달리 W_b/H가 가장 짧은 1.1이 1.4∼2.0보다 비교적 안전율이 높게 평가되었으나 일정한 경향성은 보이지 않는다.

해석결과를 종합해 보면, W_b/H 증가에 따른 안전율 변화가 일률적이진 않으나 보강길이비가 증가에 따라 안전율은 증가하는 것으로 나타났다. 즉, BTB 보강토옹벽의 안정성은 일정 이상의 옹벽폭비의 확보도 필요하지만, 무엇보다 보강길이비를 증가시키는 것이 중요하다는 것을 알 수 있다.

Fig. 8

Safety factor according to the W_b/H change

2.3 최적 보강길이비에 대한 고찰

BTB 보강토옹벽에 대해 타이백(tie-back) 및 한계평형해석(LEM)의 결과를 토대로 기준안전율을 모두 만족하는 조건에서 높이 및 옹벽폭비에 따른 최적 보강길이비를 산정하면, 옹벽높이 3.0m의 경우 W_b/H=1.1∼2.0 모두 보강길이비 0.65 이상, 5.0m의 경우 W_b/H=1.1은 보강길이비 0.65, W_b/H=1.4 이상에서는 보강길이비 0.70 이상이 가장 적정하며 7.0m의 경우 W_b/H=1.1의 조건에서는 보강길이비 0.65, W_b/H=1.4 이상에서는 보강길이비 0.75 이상을 적용하는 것이 가장 적정한 것으로 평가되었다. 10.0m의 경우는 W_b/H=2.0 이내에서는 다소 불안정한 결과를 보여 실제 설계에서는 특별한 경우를 제외하고 가급적 적용하지 않는 것을 제안한다. 이를 정리하면 Table 1과 같다.

3. 결론 및 제언

보강토옹벽의 Simple, Complex 등 다양한 형태 중에서 Back-to-Back 형태의 보강토옹벽은 좁은 구간에 양립하는 옹벽의 형식을 가지기 때문에 이격거리에 따라 보강재의 겹침이 발생한다. 이러한 겹침은 보강재 간의 상호작용에 의한 응력 변화와 일체화된 상태에서 전체 거동의 문제가 있어 설계단계에서 신중한 접근이 필요하나 현재 정형화된 설계기준이나 지침이 전무한 실정이다. 이러한 BTB 보강토옹벽의 보강길이비 및 옹벽폭비에 따른 최적 설계 조건을 알아보고자 고찰하게 되었으며 이를 통해 다음가 같은 결론을 얻었다.

(1) FHWA 설계기준을 준용한 BTB 보강토옹벽 해석은 보강길이비가 증가할수록 안전율이 매우 선형적으로 증가하고 옹벽의 높이가 높을수록 안전율이 증가하나 보강재 겹침과 상관없이 양립하는 옹벽의 한쪽 단면만을 평가하여 겹침에 따른 상호작용 및 옹벽폭비 변화를 고려하지 못하였다. 반면 한계평형해석의 경우 옹벽폭비에 따른 안전율 변화를 보이며 높이가 높을수록 안전율이 더 감소하는 것으로 나타났다.

(2) BTB 보강토옹벽의 높이가 10.0m 이상일 경우 W_b/H=2.0 이내에서는 다소 불안정한 경향을 보이므로 실제 설계에서는 신중한 접근이 필요하며 불가피할 경우 W_b/H=2.0 이상을 제안한다.

(3) BTB 보강토옹벽의 높이 및 옹벽폭비에 따른 최적 보강길이비는 2.3장에 제안하였으며, FHWA 설계기준이 한계평형해석에 비해 다소 과대하게 평가되므로 실제 설계단계에서 반드시 한계평형해석을 통한 안정성 확인이 필요하다.