1. 서 론

최근 경주, 포항 등지에서 발생한 규모 있는 지진으로 인해 댐과 같은 대형 토목구조물의 내진성능 확보가 중요한 과제가 되고 있다. 필댐의 경우 댐을 구성하는 심벽부와 사력부 및 기초 지반의 동적 거동이 댐의 내진 성능을 결정한다. 댐 구성 재료 및 기초 지반의 동적 거동은 각 재료의 전단탄성계수(or 전단파 속도, Vs)에 의해 큰 영향을 받는다. 따라서 댐체 내진성능 평가에 있어 댐을 구성하는 각 구성 요소의 신뢰할 수 있는 전단파 속도(or 전단탄성계수) 분포 결정은 매우 중요한 요소이다.

이러한 댐체의 전단파 속도(or 전단탄성계수) 분포는 현장 탄성파 시험이나 기존 연구에 의해 제시된 경험식을 통해 결정될 수 있다. 국내에서는 Sawada와 Takahashi(1975)가 일본에 위치하는 3개 댐 내부에서 계측된 실지진파 기록을 분석하여 제안한 경험식을 많이 사용한다.

대상 시스템의 전단파 속도 분포는 현장 탄성파 시험에 의해 결정될 수 있다. 탄성파 시험은 시추공을 이용하는 다운홀, 크로스홀 시험 그리고 PS-suspention logging 시험과 같은 시추공 탄성파 시험과 대상 시스템에 대한 시추공 없이 모든 감지기를 대상 시스템 표면에 설치하고 시험을 수행하는 비파괴 탄성파 시험으로 크게 구분할 수 있다. 댐 사력존의 경우 시험 수행시 대상 시스템에 대한 손상 및 시추공 형성의 어려움으로 인해 시추공 탐사보다 비파괴 탄성파 탐사가 보다 적합하며, 기울어진 사면에서 시험이 수행되어야 하는 시험의 공간적 특성으로 인해 비파괴 탄성파 탐사기법들 중 시험이 상대적으로 간편하며, 국부적인 영역 평가가 가능하고 강한 배경 잡음 조건에서도 시험이 가능한 HWAW시험(Park and Kim, 2004(a), 2004(b))이나, 기존 SASW시험(Stokoe et al., 1994)과 같은 표면파 시험이 효과적으로 사용될 수 있다(Hwang and Park, 2014; Hwang et al., 2014; Kim et al., 2009). 기존 댐들에서 수행된 탄성파 탐사들에서 결정된 결과들을 보면 전단파 속도 주상도가 댐 길이방향 위치에 따라 값의 차이를 가짐을 볼 수 있다. 즉 댐체 내부에 전단파 속도 공간 변동성이 존재함을 볼 수 있다. 또한 서로 다른 댐에서 결정된 전단파 속도 주상도들 사이에서 차이가 존재함을 볼 수 있다. 즉 댐을 구성하는 재료에는 공간에 따라 그리고 동일 유형 댐이라도 댐에 따라 전단파 속도 변동성이 존재함을 알 수 있다(Hwang et al., 2014; Park et al., 2016). 이러한 전단파 속도 변동성은 다양한 원인에 의해 발생할 수 있다. 이러한 변동성을 결정론적으로 규명하기 위해서는 매우 많은 수의 현장 시험이 필요하나, 이러한 많은 수의 시험은 댐에서 현실적으로 매우 어렵다. 이러한 댐체 내부, 댐과 댐사이에 존재하는 물성치 변동성이 반영되지 않은 대표 전단파 속도 주상도를 해석에 사용하는 경우 해석 결과에 불확실성이 발생할 수 있다. 따라서 현장 시험에서 얻어진 전단파 속도 주상도와 같은 시험결과들은 이러한 물성치 변동성에 의한 불확실성이 고려된 형태로 제시되어야 하며, 댐을 대표하는 전단파 속도 주상도 모델 또한 이러한 불확실성이 반영되어야 한다.

본 연구에서는 국내 필댐 사력부에 존재하는 물성치 변동성에 의해 발생 가능한 불확실성을 평가하고 이러한 불확실성이 고려된 국내 필댐 사력부를 위한 전단파 속도 주상도 모델을 제안하였다.

2. 댐 사력부 구성 재료에 존재하는 물성치 변동성이 고려된 사력부 전단파 속도 분포(주상도) 모델 결정 방법

필댐 내부에는 다양한 원인에 의해 구성 재료 전단파 속도의 공간적 변동성이 존재한다. 이러한 물성치 변동성에 의한 지반 조사결과의 불확실성은 대상 시스템의 다양한 위치에서 많은 수의 지반 조사가 수행될수록 감소하나 다양한 현실적 요인에 의해 일반적으로 제한된 수의 지반조사만이 수행되게 된다. 한정된 수의 지반 조사에서 얻어진 제한된 수의 전단파 속도 주상도들을 사용하여 대상 댐의 심벽부나 사력부를 대표하는 전단파 속도 주상도를 결정하고 이를 이용하여 해석을 수행하는 경우 해석결과가 실제 댐의 거동과 차이를 보일 수 있다. 이러한 해석결과의 불확실성은 몬테카를로 시뮬레이션(MCS)을 활용한 확률론적 해석에 의해 관리될 수 있다. 몬테카를로 시뮬레이션을 활용한 확률론적 해석에서는 먼저 대상 시스템에 존재 가능한 전단파 속도 주상도들을 결정한 후 이러한 주상도들을 사용하여 해석을 수행한다(Hwang and Park, 2013; Park and Hwang, 2014; Park et al., 2016a). MCS를 위한 대상 시스템에 존재 가능한 전단파 속도 주상도들은 재료 물성치의 불확실성이 반영되어 생성되게 된다. 이때 생성된 전단파 속도 주상도들은 대상 시스템 재료가 가지는 전단파 속도의 공간 변동성이 고려된 전단파 속도 주상도 모델 결정에 사용될 수 있다.

본 연구에서는 Hwang and Park(2013)에 의해 제안된 방법을 사용하여 국내 필댐 사력부 재료에 존재 가능한 전단파 속도 변동성에 의해 현장 시험에서 결정된 사력부 전단파 속도 주상도에 발생할 수 있는 불확실성을 평가하고, 이러한 불확실성이 반영된 국내 필댐 사력부에 존재 가능한 전단파 속도 주상도들을 생성·사용하여, 필댐 사력부를 위한 전단파 속도 주상도 모델을 결정하였다. Hwang and Park에 의해 제안된 방법은 현장에서 수행된 제한된 수의 시험에서 얻어진 전단파 속도 주상도들에 대해 하모닉 웨이브릿 변환(Newland, 1999)을 사용하여 댐 사력부에 존재하는 전단파 속도 공간 분포 특성을 공간-파수(space-wave number) 영역에서 분석하고 이를 활용하여 파수 성분별 크기 및 위상의 표준편차를 결정한다. 각 파수 성분이 가지는 파수의 크기는 물성치 변동 경향의 공간적 점유정도를 나타낸다. 즉 큰 파수를 가지는 성분일수록 물성치의 국부적(local) 공간에서의 변동 경향성을 표현하며, 파수가 작아질수록 전역적(global)인 공간에서의 물성치 변동 경향을 나타낸다. 파수성분 크기(에너지)의 표준 편차는 물성치 변동성에 의해 특정 위치에서 계측된 속도 값의 크기가 가질 수 있는 불확실성 크기와 관련되어 있으며, 위상의 표준편차는 물성치 변동성에 의해 계측된 속도 값의 존재 위치(깊이)가 가질 수 있는 불확실성 크기와 관련되어 있다. 즉 대상 시스템(전단파 속도 주상도)을 표현하는데 필요한 모든 파수 성분들을 구성하는 각 파수성분들이 가지는 크기의 표준편차와 위상의 표준편차가 결정되면, 대상 시스템에 존재 가능한 물성치 공간 변동성에 의해 현장시험에서 얻어진 전단파 속도 주상도에 발생할 수 있는 모든 불확실성을 확률분포형태로 표현할 수 있다. 일단 현장 시험에서 얻어진 전단파 속도 주상도에 존재하는 모든 불확실성이 결정되면, 시험에서 얻어진 전단파 속도 주상도를 구성하는 파수성분들에 앞에서 결정된 불확실성 확률분포로부터 생성된 불확실성을 부여한 후 역 하모닉 웨이브릿 변환을 적용하여 대상 시스템에 존재 가능한 전단파 속도 주상도들을 생성할 수 있다. 이러한 과정을 통해 생성된 물성치 분포들을 사용하여 대상 시스템에 대한 물성치 분포 모델을 결정하게 된다.

3. 댐 사력존 구성 재료 물성치 변동성에 의한 불확실성이 반영된 국내 필댐 사력부 전단파 속도 주상도 모델

국내 필댐 사력부에 존재하는 재료 물성치 변동성을 고려한 전단파 속도 주상도 모델을 결정하기 위해서는 개별 댐 사력부 내부에 존재하는 전단파 속도 분포의 변동성과 댐 들 사이에 존재하는 전단파 속도 주상도의 변동성(차이)이 고려되어야 한다. 일반적으로 동일 유형 댐들이라도 댐들 사이의 물성치 변동성이 댐 내부에 존재하는 변동성보다 크다(Park et al., 2016b). 따라서 댐 사이 물성치 변동성을 고려하여 결정된 깊이별 전단파 속도 상한 값과 하한 값으로 표시되는 전단파 속도 주상도 모델은 댐 내부 변동성을 고려해 결정된 전단파 속도 모델을 포함하게 된다. 따라서 본 연구에서는 일반적인 국내 필댐 사력부 전단파 속도 모델 결정을 위해 9개의 개별적인 댐에서 결정된 전단파 속도 주상도들을 사용하여 댐들 사이에 존재하는 변동성을 평가·사용하였다.

3.1 댐 사이에 존재하는 물성치 변동성에 의해 전단파 속도 주상도에 발생 가능한 불확실성 평가

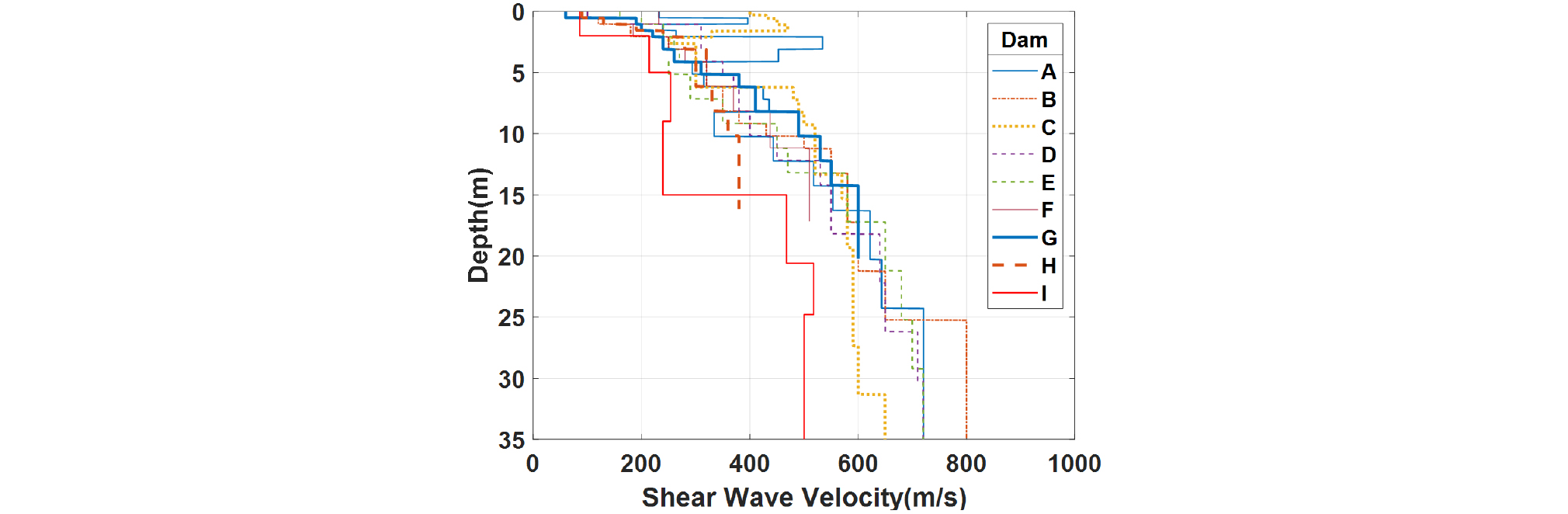
본 연구에서 시험을 통해 결정된 I 댐(Fig. 1)의 전단파 속도 주상도와 기존 연구에서 결정된 8개 댐(A~H댐)(Kim et al., 2009)의 전단파 주상도들을 활용하여 댐 사이에 존재하는 사력부 전단파 속도 분포의 변동성(또는 불확실성)을 평가하였다. Fig. 2는 사용된 전단파 속도 주상도들이다. 그림에서 C, D, H, I 댐의 전단파 속도 주상도들은 HWAW 방법에 의해 결정되었으며, A, B, E, F, G 댐들은 SASW방법에 의해 결정된 주상도 들이다. 그림을 보면 전단파 속도 주상도들이 서로 차이(변동성)를 보임을 알 수 있다.

Fig. 1.

HWAW test in I dam

Fig. 2.

Vs profiles of rockfilled zone of fill dam

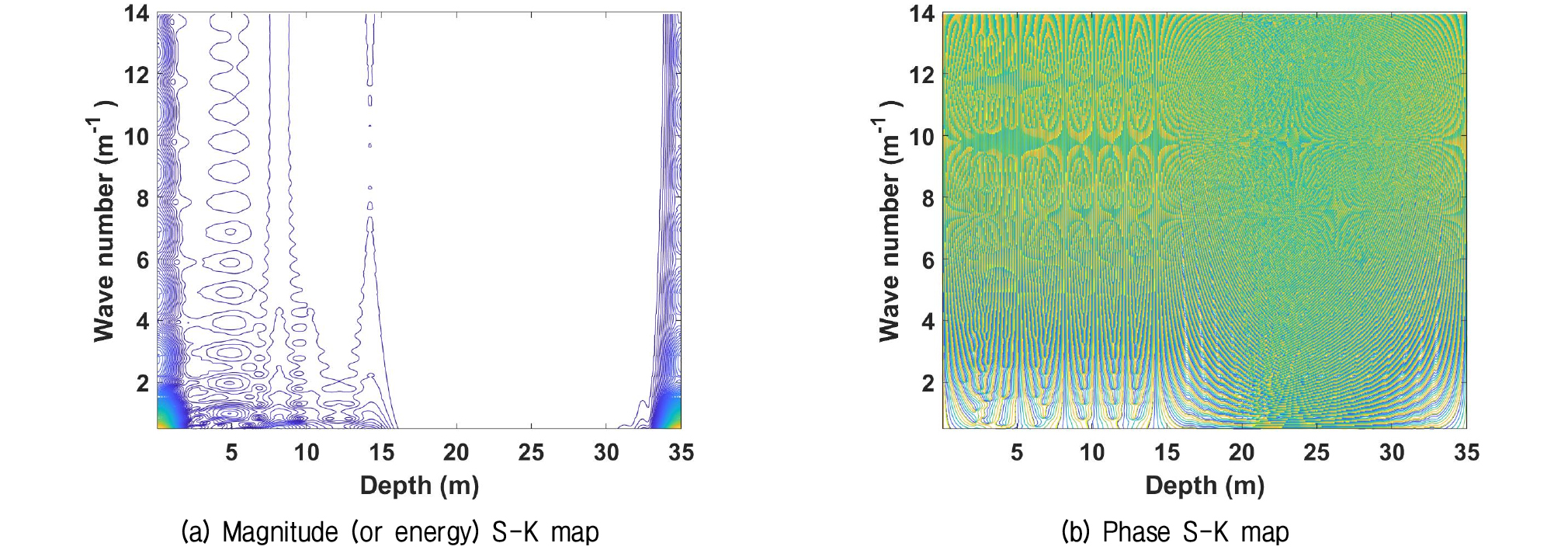
Fig. 3은 E댐 사력부에서 시험을 통해 결정된 전단파 속도 주상도에 대한 하모닉 웨이브릿 변환을 통해 결정된 공간-파수 영역에서의 전단파 속도 분포 구조 이다. 이 그림은 공간(or 깊이)-파수 영역에서 각 파수성분의 크기(에너지)와 위상을 등고선 지도(contour map) 형태로 나타낸다.

Fig. 3.

Magnitude (or energy) and phase space(S)-wave number(K) map of Vs profile of E dam

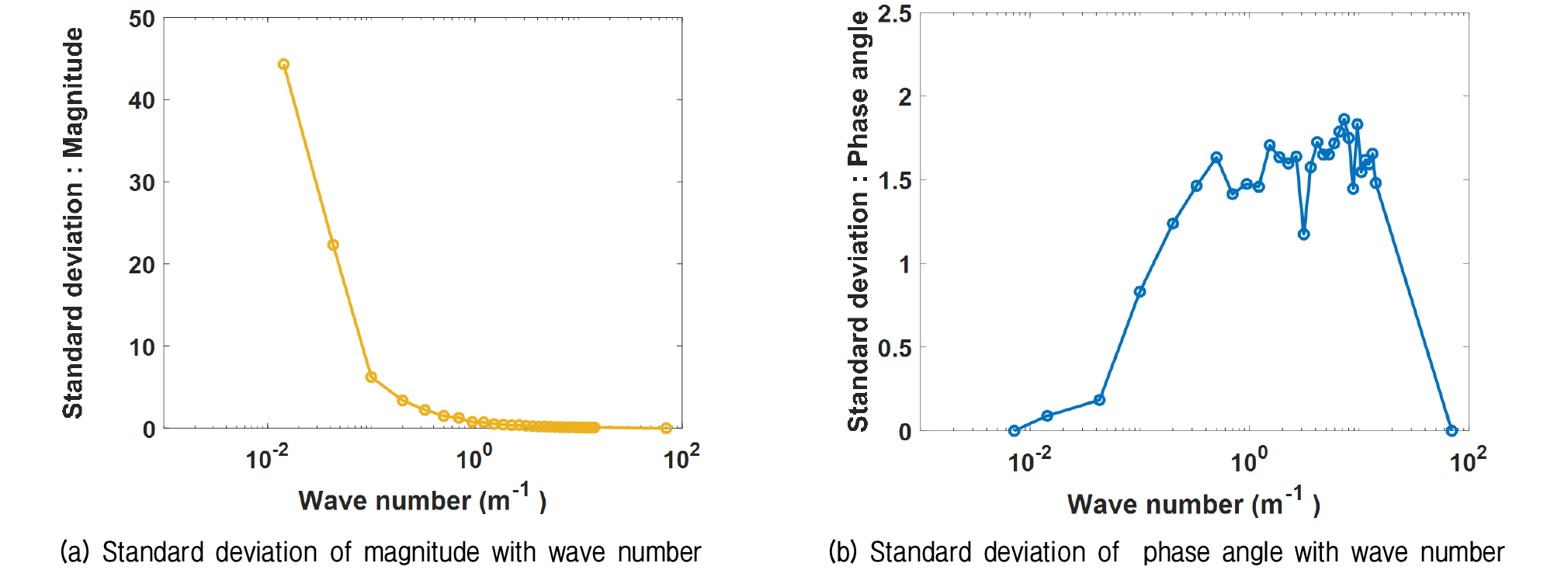
Fig. 4는 Fig. 2에서 제시된 국내 9개 댐에서 수행된 시험 결과들에 대해 2절에서 제안된 방법에 따라 결정된 전단파 속도 분포의 파수 성분별 크기 및 위상의 표준편차이다. Fig. 4에 주어진 파수 성분별 크기 및 위상의 표준편차는 댐들에서 결정된 전단파 속도 주상도들 사이에 존재하는 변동성에 의해 주어진 하나의 대표 전단파 속도 주상도 또는 주상도 모델에서 발생할 수 있는 모든 불확실성을 나타낸다.

Fig. 4.

Uncertainties in structure of shear wave velocity profile of rockfilled zone among fill dams

3.2 재료 물성치 변동성에 의한 불확실성이 고려된 국내 필댐 사력부의 전단파 속도 주상도 모델

본 절에서는 통계적인 방법에 의한 국내 필댐 사력부 전단파 속도 주상도 모델 결정을 위해 필요한 사력부에 존재 가능한 충분한 수의 깊이-전단파 속도 곡선들을 생성하였다. 이를 위해 3.1절에서 결정된 사력부 재료에 존재하는 전단파 속도 변동성(or 불확실성)과 2절에서 제시된 방법에 따라 사력부에 존재 가능한 400개의 깊이-전단파속도 곡선들을 결정하였다.

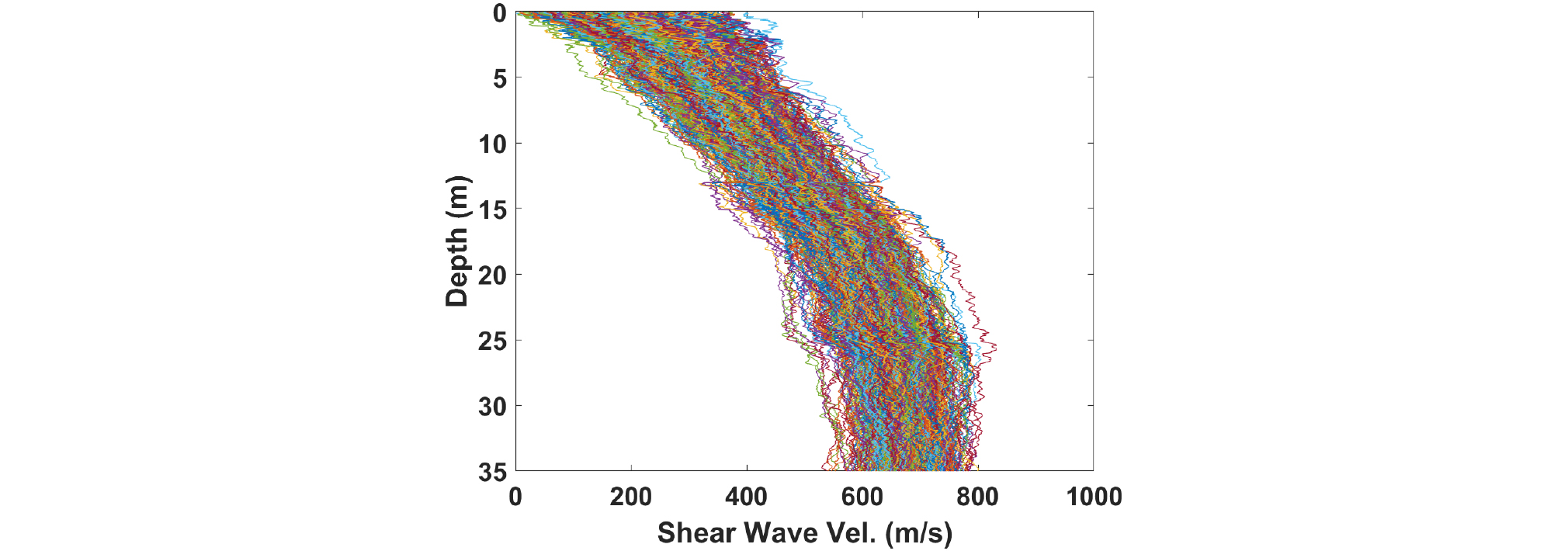
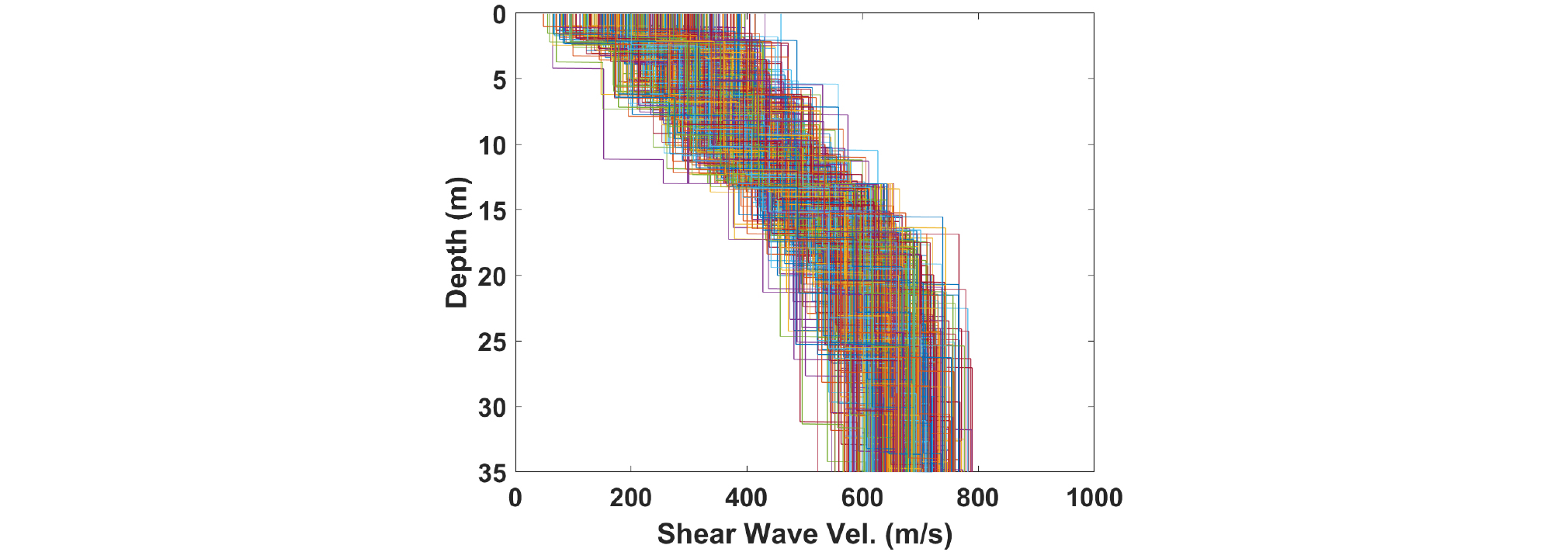
Fig. 5는 결정된 400개의 깊이-전단파 속도 곡선들을 모두 그린 그림이다. 이 곡선들은 댐 사이 물성치 변동성에 의한 불확실성이 모두 반영된 사력부에 존재 가능한 깊이-전단파 속도 곡선들이다. 각각의 곡선들이 가지는 존재 확률의 크기는 모두 같으나 각 깊이에서 전체 곡선들의 속도가 전체 속도 범위(대역)에 걸쳐 균등하게 존재하는 것이 아니라 특정 속도 대역에 집중된 형태로 존재함을 볼 수 있다. 이러한 깊이별 전단파 속도 분포로부터 각 깊이에서의 전단파 속도 상한과 하한을 결정할 수 있다.

Fig. 5.

Possible depth-Vs curves in the rockfilled zone of fill dams

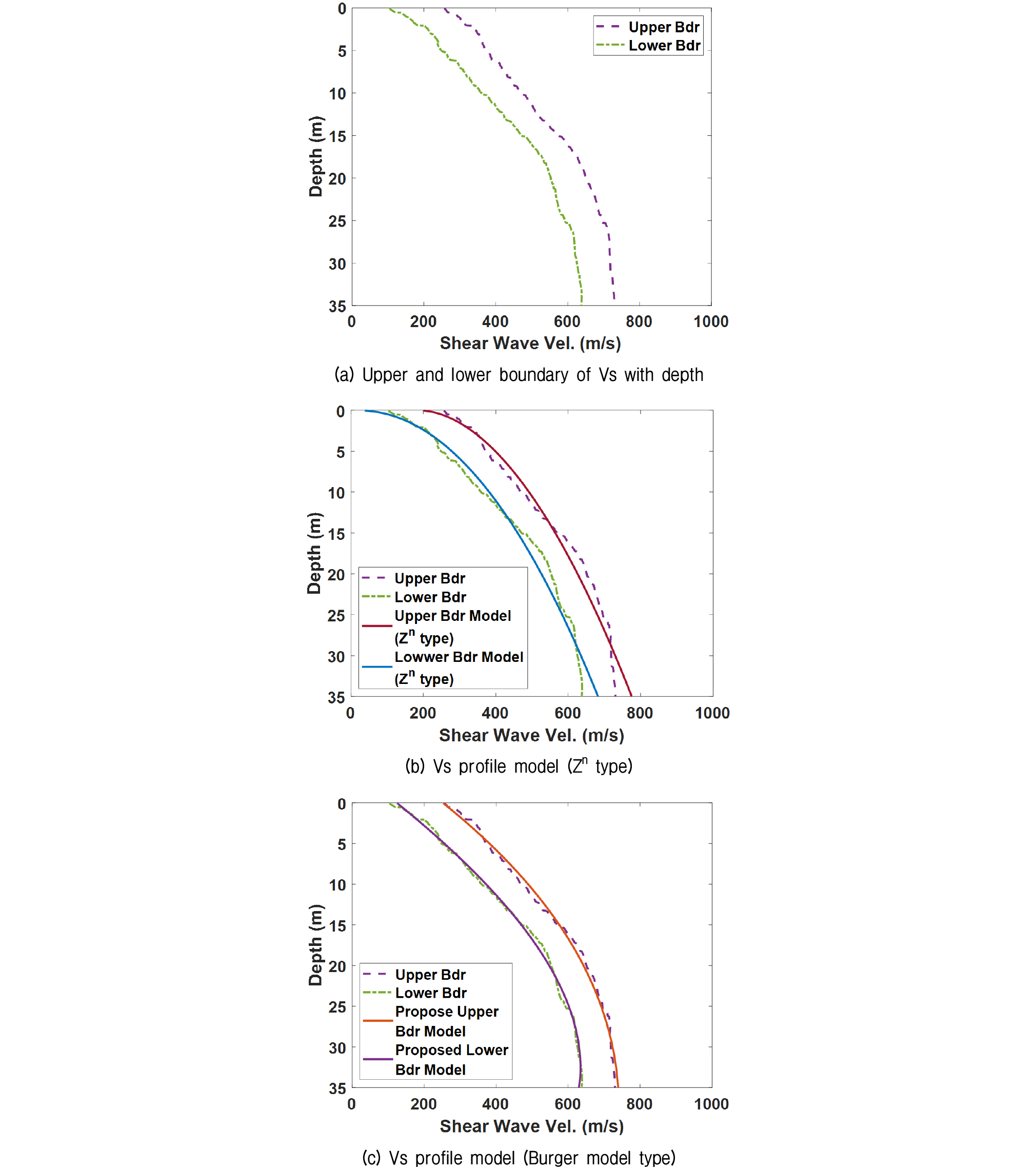
Fig. 6(a)는 Fig. 5에서 얻어진 속도 곡선들에서 결정된 각 깊이별 속도값 상한과 하한을 나타낸 그림이다.

이때 깊이별 전단파 속도 상한과 하한은 각 깊이에 존재 가능한 전단파 속도값 분포에서 결정된 평균과 표준편차에 의해 결정되었다. 즉 상한은 [평균+(1×표준편차)]이며 하한은 [평균-(1×표준편차)]에 의해 결정된다. 각 깊이에서 주어지는 속도값 상한과 하한은 그 깊이에서 존재 가능한 전단파 속도값들 중 68%가 위치하게 되는 속도 범위의 경계를 나타낸다. 만일 평균을 중심으로 ±(2×표준편차)를 사용하여 상한과 하한을 결정하게 되면 결정된 상한과 하한 사이의 속도대역은 주어진 깊이에서 95% 확률로 전단파 속도값이 존재하게 되는 범위를 나타낸다. 앞에서 결정된 깊이별 속도 상한과 하한 곡선에 대해 비선형 회귀분석을 수행하여 국내 필댐 사력부 전단파 속도 주상도 상한과 하한 모델을 결정하였다. 일반적으로 많이 사용되는 Sawada-Takahashi 모델식은 전단파 속도가 (깊이)ⁿ에 단순 비례하는 형태로 표현된다. 이러한 형태는 전단파 속도가 구속압에 비례한다는 결과에 기인한다. 이러한 형태 모델식을 기반으로 Fig. 6(a)에 적합한 모델식을 비선형 회귀분석을 통해 결정하면 Fig. 6(b)와 같은 형태가 얻어지며, 모델식은 다음과 같다.

Fig. 6.

Upper and lower boundary of shear wave velocity with depth and Vs boundary model for rockfilled zone of fill dams

그림을 보면 결정된 모델이 전단파 속도 상한과 하한의 깊이에 따른 변화 경향을 어느정도 따라가나 깊이에 따라 유의미한 차이를 보인다. Fig. 6(a)에 주어진 전단파 속도 상한과 하한 곡선은 대략 15m 깊이에서부터 깊이 증가에 따른 전단파 속도 증가율이 상대적으로 감소하며 25m 깊이에서부터는 증가율이 매우 작은 값을 가지게 된다. Fig. 6(b)를 보면 식 (1)에 주어진 모델식이 이러한 경향을 제대로 표현하지 못함을 볼 수 있다. 이러한 깊이에 따른 전단파 속도 변화 특성은 일반적인 반무한 지반과 달리 댐의 형태가 가진 특성에 의해 구속압이 단순한 형태로 깊이에 비례하는 것이 아니라 보다 복잡한 형태로 깊이에 비례하기 때문인 것으로 생각된다. 따라서 본 연구에서는 (깊이)ⁿ 비례 형태 모델식과 함께 깊이에 따른 전단파 속도 상한과 하한을 가장 잘 표현할 수 있는 모델식을 제안하였다. 제안된 모델의 형태는 Maxwell과 Kelvin-Voit 모델로 구성된 Burger 모델로서 다음과 같이 결정되었으며, Fig. 6(c)에 나타내었다.

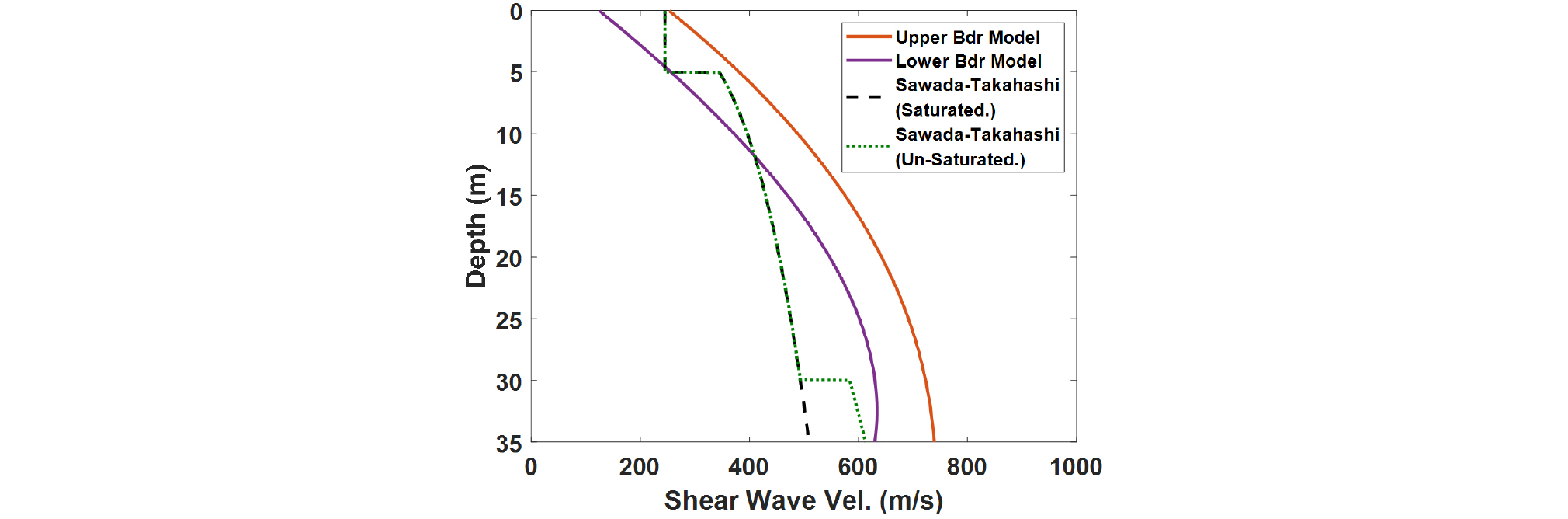
제안된 모델식은 국내 필댐 사력존 전단파 속도의 깊이에 따른 상한과 하한 곡선을 통계적으로 가장 잘 나타내는 표현형이다. 모델식의 형태 및 모델을 구성하는 계수들이 가지는 물리적인 의미는 Burger 모델을 구성하는 각 요소들이 가지는 물리적인 의미와 동일하지는 않다. 이 모델식의 형태는 앞에서 언급한 바와 같이 댐의 기하학적 구조에 기인하는 깊이 증가에 따른 구속압 증가 특성 및 재료 특성에 기인한 것으로 생각된다. 그림을 보면 이 모델식은 35m 깊이까지는 사력존 전단파 속도 분포를 합리적으로 잘 표현하나 35m 이상 깊이에서 적용 시 하한 모델은 대상을 합리적으로 표현 못할 수 있다. 이때 Z(m)는 깊이이다. Fig. 7에서 제안된 모델과 일반적으로 많이 사용되는 Sawada-Takahashi 모델을 비교하였다.

Fig. 7.

Comparison of proposed model and Sawada-Takahashi model

그림을 보면 제안된 모델과 Sawada-Takahashi 모델은 12m 깊이까지는 유사한 속도 범위를 보인다. 깊이에 따른 전단파 속도 증가율은 22m 깊이까지는 제안된 모델이 Sawada-Takahashi 모델에 비해 상대적으로 큼을 볼 수 있다. 그러나 22m 이상 깊이에서는 깊이에 따른 증가율이 매우 비슷함을 볼 수 있다. 제안된 모델에 의한 전단파 속도는 Sawada-Takahashi 모델에 비해 대략 깊이 12m 이상에서는 큼을 볼 수 있다. 이러한 차이는 Sawada-Takahashi 모델이 댐에 설치된 지진계에서 계측된 실지진파 기록을 사용하여 전단파 속도를 결정하였기 때문으로 생각된다. 본 연구에서 표면파 기법을 사용하여 결정된 전단파 속도 주상도들은 미소변형율 영역에서 결정된 최대 전단파 속도인데 반하여 실지진파를 사용하여 결정된 Sawada-Takahashi 모델의 경우 중간변형율 영역(미소변형율에 비해 작은 전단탄성계수값(전단탄성계수)을 보임)에서 결정된 전단파 속도일 가능성이 크기 때문이다.

Fig. 5에서 보여진 국내 필댐 사력존에 존재 가능한 깊이-전단파 속도 곡선들은 Fig. 8과 같은 사력존에 존재 가능한 전단파 속도 주상도들을 생성하는 데도 사용될 수 있다. Fig. 8에 주어진 각각의 전단파 속도 주상도들은 동일한 존재 확률을 가지며, 이러한 전단파 속도 주상도들은 확률론적 해석을 위한 MCS에 사용될 수 있다.

Fig. 8.

Possible Vs profiles in the rockfilled zone of fill dams for MC.

국내 필댐 사력존 전단파 속도 주상도 모델 결정을 위해 결정된 공간 변동성에 의한 불확실성은 개별 댐에도 적용 가능하다. 즉 개별 댐에서 결정된 사력존 전단파 속도 주상도를 대표 주상도로 하여 3.1장에서 결정된 불확실성을 적용하면 각 개별 댐에 존재 가능한 전단파 속도 주상도들의 결정이 가능하다. 이를 통해 개별 댐 사력존을 위한 깊이별 전단파 속도 하한 값과 상한 값을 제공할 수도 있다(Park et al., 2016b; Hwang et al., 2014).

4. 결 론

본 연구에서는 국내 필댐 사력부 전단파 속도 주상도 결정시 사력부 재료에 존재하는 물성치 변동성에 의해 발생 가능한 불활실성을 평가하였다. 그리고 이러한 불확실성이 반영된 국내 필댐 사력부를 위한 전단파 속도 주상도 모델식을 제안하였다.

(1) 제안된 전단파 속도 주상도 모델식은 국내 필댐 사력부에 동일한 확률로 존재 가능한 400개의 깊이-전단파 속도 곡선들을 생성하고 생성된 곡선들에 대한 통계적 분석을 통해 결정되었다. 제안된 모델식은 깊이별 전단파 속도 상한과 하한값을 제공하게 된다.

(2) 필댐 사력존에서의 깊이별 전단파 속도 상한과 하한을 가장 잘 나타내기 위한 표현형으로 Burger 모델을 사용하여 전단파 속도 주상도 모델식을 결정하였다.

(3) 결정된 모델식은 일반적으로 많이 사용되는 Sawada-Takahashi 모델과 비교하였다. 제안된 모델식에 의한 전단파 속도값은 대략 12m 깊이까지는 Sawada-Takahashi 모델과 비슷한 속도대역을 가지나 그 이상 깊이에서는 더 큰 값을 가진다. 또한 대략 22m 깊이까지는 Sawada-Takahashi 모델에 비해 깊이변화에 대한 전단파 속도 변화율이 상대적으로 큰 값을 보이며 그 이상 깊이에서는 비슷한 변화율을 보인다.