Numerical Formulation of Axisymmetric Shell Element and Its Application to Geotechnical Problems

Hosung Shin; Jin-Wook Kim

doi:10.7843/kgs.2020.36.12.27

Preview

Research Article

Journal of the Korean Geotechnical Society. 31 December 2020. 27-34
https://doi.org/10.7843/kgs.2020.36.12.27

Numerical Formulation of Axisymmetric Shell Element and Its Application to Geotechnical Problems

축대칭 쉘 요소의 유한요소 수식화와 지반공학적 활용

Hosung Shin¹

Jin-Wook Kim²^†

신 호성¹

김 진욱²^†

¹Member, Prof., Dept. of Civil & Environmental Engrg., Univ. of Ulsan

²Member, Ph.D. Candidate, Dept. of Civil & Environmental Engrg., Univ. of Ulsan

¹정회원, 울산대학교 건설환경공학부 교수

²정회원, 울산대학교 건설환경공학부 박사과정

^*shingeo@ulsan.ac.kr

ABSTRACT

Use of axisymmetric shell element for the structure increases the efficiency and accuracy in finite element analysis of the interaction between the ground and the structure. This paper derived the force balance equation and the moment balance equation for an axisymmetric shell element based on Kirchhoff's theory. The governing equation for the axial deformation used the isoparametric shape function in the Galerkin formulation, and the governing equation for the shell bending used the higher-order shape function. The developed axisymmetric shell element was combined with Geo-COUS, a geotechnical finite element program for the coupled analysis with the ground. The accuracy of the developed element was confirmed through the example analyses of the circular plate and the liquid storage tank. And the energy balance equation for the axisymmetric shell element is presented.

Keywords

Axisymmetric shell element

FEM

Soil-structure interaction

구조물에 대한 축대칭 쉘요소는 지반과 구조물의 상호작용에 대한 유한요소해석에서 효율성과 정확성을 높이게 된다. 본 논문에서는 Kirchhoff 이론에 근거한 축대칭 쉘요소의 힘평형 방정식과 모멘트 평형 방정식을 유도하였다. 축방향 변형에 대한 지배방정식은 등매개변수 형상함수를 이용한 Galerkin 수식화를 수행하고, 휨에 대한 지배방정식은 고차의 형상함수를 이용하였다. 개발된 축대칭 쉘요소는 지반과의 연계해석을 위하여 지반해석 유한요소 프로그램인 Geo-COUS에 결합하였다. 원형판과 액체 저장 탱크에 대한 예제해석을 통하여 개발된 요소의 정확성을 확인하였다. 그리고 축대칭 쉘요소에 대한 에너지 평형방정식을 제시하였다.

MAIN

1. 서 론
2. 축대칭 쉘요소의 유한요소 수식화
2.1 축대칭 쉘요소의 지배방정식
2.2 축대칭 쉘요소의 Galerkin 수식화
3. 수치해석 예제
3.1 등분포 하중이 작용하는 원형판
3.2 액체 저장 탱크와 지반의 상호작용
4. 결 론

1. 서 론

지반과 구조물의 상호작용에 대한 수치해석에서 쉘 요소는 다양한 형태의 구조물 해석에 이용되고 있다. 구조공학 분야에서 원자력발전소의 철근콘크리트 격납건물과 같은 원통형 및 구형 구조물 뿐만 아니라, 지반공학 분야에서 축대칭 해석시 포함되는 다양한 형태의 구조물를 해석하기 위하여 축대칭 쉘 요소(axisymmetric shell element)가 필요하다. 하지만, 지반공학 분야에서 주로 사용되는 상용프로그램들이 축대칭 해석에서 축대칭 구조물 요소를 제공하지 않거나 수치적인 정확도가 부족하여(PLAXIS, 2018), 주로 축대칭 연속체 요소를 이용하여 구조물 해석을 수행하게 된다. 이러한 구조물에 대한 연속체 해석 결과는 많은 요소가 필요함에도 높은 세장비로 해석결과의 정확도가 낮아지며, 구조물의 부재력을 산정하기 위하여 추가적인 선형보간을 수행해야 하는 단점이 있다.

Flügge(1932)가 원통형 쉘의 변위에 대한 지배 미분방정식을 유도하고(Flügge, 1973), Grafton과 Strome(1963)가 유한요소법(Finite element method)을 이용하여 원뿔형 절두체(conical frustra) 변위해석을 수행하였다. Jones와 Strome(1966)는 곡선의 축대칭 쉘 요소를 개발하고, Prathap과 Ramesh Babu(1986)는 3절점의 2차 곡선 축대칭 쉘 요소를 제안하였다.

본 논문에서는 축대칭 쉘의 힘평형 방정식을 유도하고 임의 형상에 대한 Galerkin 수식화를 수행하였다. 개발된 축대칭 쉘요소를 유한요소 프로그램에 결합하고 지반과 구조물의 상호작용에 대한 예제해석을 통하여 개발된 요소의 정확성과 안정성을 확인하고자 한다.

2. 축대칭 쉘요소의 유한요소 수식화

2.1 축대칭 쉘요소의 지배방정식

쉘(shell)은 두께가 다른 폭에 비하여 대단히 얇아서 Kirchhoff 이론에 근거하여 전단변형을 무시하고 휨 변형만을 고려하는 구조 요소이다. 따라서 변형 전의 중립면에 수직인 직선은 변형 후에도 중립면에 수직을 유지하므로, 중립면에 수직인 직선의 회전각은 중립면의 기울기 변화와 동일하다.

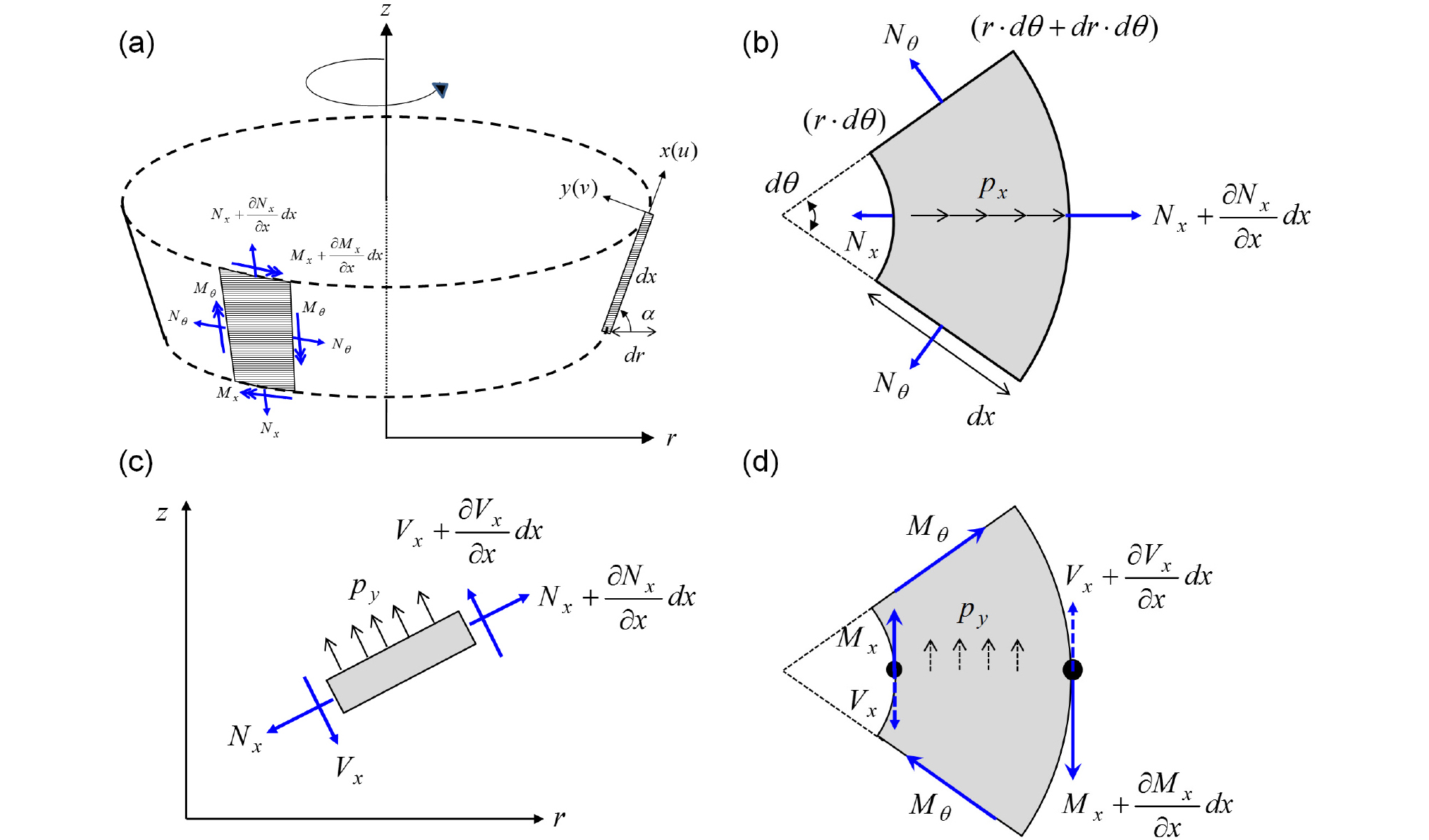
국부 좌표계 (x, y)에서 축대칭 쉘요소의 변위량은 (u, v)로 표현하였다(Fig. 1(a)). 미소 변형에 대하여 축대칭 쉘의 변형률과 변위는 다음과 같은 관계가 있다(Flügge, 1973; Timoshenko and Woinowsky-Krieger, 1959).

https://static.apub.kr/journalsite/sites/kgs/2020-036-12/N0990361203/images/kgs_36_12_03_F1.jpg

Fig. 1

(a) Geometric configuration of the shell segment, (b) Force equilibrium of local axial direction (x) on the top view of Figure a, (c) Force equilibrium of local tangential direction (y) on the front view, (d) Moment equilibrium on the shell surface on the top view

(1)

ε_{x} = \frac{d u}{d x}, ε_{θ} = \frac{u \cdot \cos (α) - v \cdot \sin (α)}{r} χ_{x} = \frac{d^{2} v}{d x^{2}}, χ_{θ} = \frac{d v}{d x} \cdot \frac{\cos (α)}{r}

축대칭 쉘 요소의 응력과 변형률의 관계는 선형탄성 재료(E=탄성계수, ν=포아송 비, h=쉘의 두께)에서 식 (2)와 같이 정의된다.

(2)

N_{x} = D^{a} (ε_{x} + ν \cdot ε_{θ}), N_{θ} = D^{a} (ε_{θ} + ν \cdot ε_{x}) M_{x} = D^{b} (χ_{x} + ν \cdot χ_{θ}), M_{θ} = D^{b} (χ_{θ} + ν \cdot χ_{x})

여기서, x는 요소의 축방향(axial direction)을 나타내고, θ는 원주 방향(circumferential direction)을 의미한다. 여기서, D^a = E · h / (1 - ν²)이며, D^b = E · h³ / 12(1 - ν²)이다.

Fig. 1(b)는 3차원 요소의 상면도에서 원주 방향으로 dθ의 크기를 갖는 요소에 축방향(x)으로 작용하는 전체 힘을 도시하고 있다.

(3)

- N_{x} \cdot r \cdot d θ + (N_{x} + \frac{d N_{x}}{d x}) (r \cdot d θ + d r \cdot d θ) - 2 N_{θ} \cdot d x \cdot \sin (d θ / 2) + p_{x} \cdot r \cdot d x \cdot d θ = 0

요소의 기울기 α는 cos(α) = dr / dx과 같으므로 요소의 축방향 힘평형 방정식은 다음과 같다.

(4)

\frac{d (r \cdot N_{x})}{d x} - N_{θ} \cdot \cos (α) + p_{x} \cdot r = 0

여기서, p_x는 요소에 축방향으로 작용하는 단위면적당 하중이다.

Fig. 1(c)는 3차원 요소의 정면도에서 축대칭 쉘요소에 직교방향(normal direction, y)으로 작용하는 힘을 나타내고 있다.

(5)

- V_{x} \cdot r \cdot d θ + (V_{x} + \frac{d V_{x}}{d x} d x) (r \cdot d θ + d r \cdot d θ) + 2 N_{θ} \cdot d x \cdot \sin (d θ / 2) \cdot \sin (α) + p_{y} \cdot r \cdot d x \cdot d θ = 0

식 (5)를 정리하면, 축대칭 쉘요소의 직교방향(y)에 대한 힘평형 방정식은 다음과 같다.

(6)

\frac{d (r \cdot V_{x})}{d x} + N_{θ} \cdot \sin (α) + P_{y} \cdot r = 0

여기서, p_y는 쉘요소에 연직한 단위면적당 작용하는 하중이다.

Fig. 1(d)는 3차원 요소의 상면도에서 축대칭 쉘요소의 면에 작용하는 전체적인 모멘트를 나타내고 있다.

(7)

- M_{x} \cdot r \cdot d θ + (M_{x} + \frac{d M_{x}}{d x} d x) (r \cdot d θ + d r \cdot d θ) + (V_{x} + \frac{d V_{x}}{d x} d x) (r \cdot d θ + d r \cdot d θ) \cdot d x - 2 M_{θ} \cdot d x \cdot \sin (d θ / 2) \cdot \cos (α) + p_{y} \cdot r \cdot d x \cdot d θ \cdot d x / 2 = 0

그리고 축대칭 쉘요소에 대한 모멘트 평형 방정식은 다음과 같다.

(8)

\frac{d (r \cdot M_{x})}{d x} - M_{θ} \cdot \cos (α) + r \cdot V_{x} = 0

축대칭 쉘요소의 전단면에 작용하는 전단응력은 식 (6)과 식 (8)로부터 국부 좌표계의 변위량 (u, v)을 이용하여 산정할수 있다.

(9)

V_{x} = - D^{b} \cdot (χ_{x} - χ_{θ}) \frac{r}{\cos (α)} - D^{b} \cdot \frac{d^{3} v}{d x^{3}}

2.2 축대칭 쉘요소의 Galerkin 수식화

축대칭 쉘요소의 지배방정식들에 Galerkin 수식화를 적용하여 각 요소의 국부 좌표계에서의 변위량 (u, v)에 대한 근사적인 방정식을 얻을수 있다.

첫번째, 쉘요소의 축방향 힘평형 방정식(식 (4))에 가중함수(w^a)를 적용하여 근사해를 산정하는 Galerkin 수식은 다음과 같다.

(10)

\int_{x} w^{a} \cdot [\frac{d}{d x} (r \cdot N) - N_{θ} \cdot \cos (α) + p_{x} \cdot r] d x = 0

첫째 항에 그린-가우스 부분적분으로 적용하여 정리하면 식 (11)과 같다.

(11)

\int_{x} \frac{d w^{a}}{d x} (r \cdot N_{x}) d x + \int_{x} w^{a} \cdot N_{θ} \cdot \cos (α) d x = \int_{Γ} n_{x} w^{a} (r \cdot N_{x}) d Γ + \int_{x} w^{a} \cdot (p_{x} \cdot r) d x

여기서, $\int_{Γ} n_{x} w^{a} (r \cdot N_{x}) d Γ$ 는 요소의 경계에 대한 적분이다.

식 (11)의 Galerkin 수식에 Newton의 반복과정을 이용할 수 있도록 t⁽ⁿ⁺¹⁾에서의 부재력을 국부 좌표계에서의 변위 증분(du, dv)을 이용하여 산정하였다.

(12)

N_{x}^{(n + 1)} \approx N_{x}^{(n, i)} + D^{a} \cdot \frac{d (d u)}{d x} + D^{a} \cdot ν \cdot \frac{\cos (α)}{r} d u - D^{a} \cdot ν \cdot \frac{\sin (α)}{r} d v N_{θ}^{(n + 1)} \approx N_{θ}^{(n, i)} + D^{a} \cdot ν \cdot \frac{d (d u)}{d x} + D^{a} \cdot \frac{\cos (α)}{r} d u - D^{a} \cdot \frac{\sin (α)}{r} d v

따라서, 쉘요소의 축방향 힘평형 방정식에 대한 Galerkin 수식화는 다음과 같다.

(13)

\int_{x} \frac{d w^{a}}{d x} (r \cdot D^{a} \cdot \frac{d (d u)}{d x}) d x + \int_{x} \frac{d w^{a}}{d x} (D^{a} \cdot ν \cdot \cos (α) d u) d x - \int_{x} \frac{d w^{a}}{d x} (D^{a} \cdot ν \cdot \sin (α) d v) d x + \int_{x} w^{a} \cdot (D^{a} \cdot ν \cdot \cos (α) \cdot \frac{d (d u)}{d x}) d x + \int_{x} w^{a} \cdot (D^{a} \cdot \frac{\cos^{2} (α)}{r} d u) d x - \int_{x} w^{a} \cdot (D^{a} \cdot \frac{\sin (α) \cdot \cos (α)}{r} d v) d x = \int_{x} w^{a} \cdot (p_{x} \cdot r) d x - \int_{x} \frac{d w^{a}}{d x} (r \cdot N_{x}^{(n, i)}) d x - \int_{x} w^{a} \cdot N_{θ}^{(n, i)} d x

두번째, 쉘요소의 휨에 대반 지배방정식은 식 (6)과 식 (8)을 결합하여 다음과 같이 표현할 수 있다.

(14)

\frac{d^{2} (r \cdot M_{x})}{d x^{2}} - \frac{d M_{θ}}{d x} \cdot \cos (α) - N_{θ} \cdot \sin (α) - p_{y} \cdot r = 0

휨에 대한 지배방정식에 가중함수(w^b)를 적용하여 Galerkin 수식화에 의한 근사식을 산정하였다.

(15)

\int_{x} w^{b} \cdot [\frac{d^{2} (r \cdot M_{x})}{d x^{2}} - \frac{d M_{θ}}{d x} \cdot \cos (α) - N_{θ} \cdot \sin (α) - p_{y} \cdot r] d x = 0

첫째와 두번째 항에 그린-가우스 부분적분으로 적용하고 요소의 경계에 대한 항목을 정리하면 다음과 같다. 쉘요소에 작용하는 하중은 대부분은 요소면에 작용하는 분포하중이고, 요소 경계에 작용하는 하중은 유한요소 프로그램에서 외부하중으로 처리할수 있으므로 요소 경계에 대한 항목을 삭제하여 식 (16)과 같이 정리할수 있다.

(16)

\int_{x} \frac{d^{2} w^{b}}{d s^{2}} \cdot (r \cdot M_{x}) d x + \int_{x} \frac{d w^{b}}{d x} \cdot M_{θ} \cdot \cos (α) d x - \int_{x} w^{b} \cdot N_{θ} \cdot \sin (α) d x = \int_{x} w^{b} \cdot p_{y} \cdot r d x

Galerkin 수식에 Newton의 반복과정을 이용할 수 있도록 t⁽ⁿ⁺¹⁾에서의 부재력을 국부 좌표계에서의 변위 증분(du, dv)로 표현하였다.

(17)

M_{x}^{(n + 1)} \approx M_{x}^{(n, i)} + D^{b} \cdot \frac{d^{2} (d v)}{d x^{2}} + D^{b} \cdot ν \cdot \frac{\cos (α)}{r} \frac{d (d v)}{d x} M_{θ}^{(n + 1)} \approx M_{θ}^{(n, i)} + D^{b} \cdot ν \cdot \frac{d^{2} (d v)}{d x^{2}} + D^{b} \cdot \frac{\cos (α)}{r} \frac{d (d v)}{d x}

따라서, 쉘요소의 휨에 대한 Galerkin 수식화는 다음과 같다.

(18)

\int_{x} \frac{d^{2} w^{b}}{d x^{2}} \cdot (D^{b} \cdot r \cdot \frac{d^{2} (d v)}{d x^{2}}) d x + \int_{x} \frac{d^{2} w^{b}}{d x^{2}} \cdot (D^{b} \cdot ν \cdot \cos (α) \frac{d^{2} (d v)}{d x}) d x + \int_{x} \frac{d w^{b}}{d x} \cdot (D^{b} \cdot ν \cdot \cos (α) \cdot \frac{d^{2} (d v)}{d x^{2}}) d x + \int_{x} \frac{d w^{b}}{d x} \cdot (D^{b} \cdot \frac{\cos^{2} (α)}{r} \frac{d (d v)}{d x}) d x - \int_{x} w^{b} \cdot (D^{a} \cdot ν \cdot \sin (α) \cdot \frac{d (d u)}{d x}) d x - \int_{x} w^{b} \cdot (D^{a} \cdot \frac{\cos (α) \cdot \sin (α)}{r} \cdot d u) d x + \int_{x} w^{b} \cdot (N_{θ}^{(n, i)} + D^{a} \cdot \frac{\sin^{2} (α)}{r} d v) d x = \int_{x} w^{b} \cdot p_{y} \cdot r d x - \int_{x} \frac{d^{2} w^{b}}{d x^{2}} \cdot (r \cdot M_{x}^{(n, i)}) d x - \int_{x} \frac{d w^{b}}{d x} \cdot (M_{θ}^{(n, i)} \cdot \cos (α)) d x + \int_{x} w^{b} \cdot (N_{θ}^{(n, i)} \cdot \sin (α)) d x

식 (1)의 축대칭 쉘의 변형률과 변위에서 쉘요소에 축방향 변위 u는 C₀ 연속성만을 요구하므로 요소의 기하학적 형상과 변위에 대하여 동일한 등매개변수(Isoparametric) 형상함수(N^a)를 사용할수 있다. 하지만, 쉘요소에 직교하는 변위 v는 C₁ 연속성이 만족되어야 하므로 고차의 형상함수(N^b)를 필요로 한다.

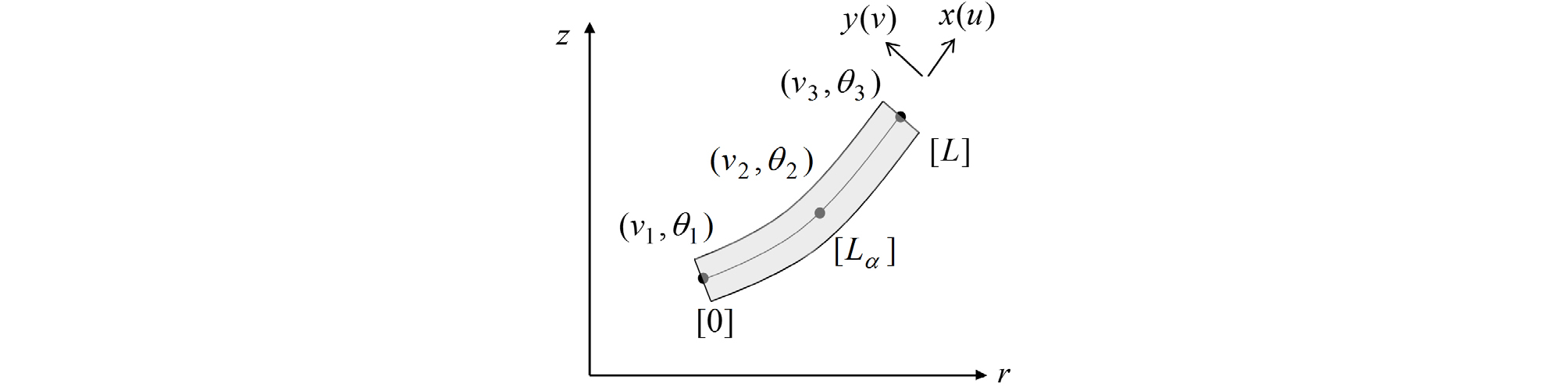
Fig. 2와 같은 3절점 축대칭 쉘요소에서 직교방향의 변위 v에 대한 형상함수(N^b)는 다음과 같다.

https://static.apub.kr/journalsite/sites/kgs/2020-036-12/N0990361203/images/kgs_36_12_03_F2.jpg

Fig. 2

Geometry and node numbering in axisymmetric shell element with 3-nodes (Length to mid-node, L_α=α·L)

(19)

N_{1}^{b} = \frac{1}{L^{5}} \frac{2 (α + 1)}{α^{3}} x^{5} - \frac{1}{L^{4}} \frac{4 α^{2} + 7 α + 4}{α^{3}} x^{4} + \frac{1}{L^{3}} \frac{2 (α + 1) (α^{2} + 3 α + 1)}{α^{3}} x^{3} - \frac{1}{L^{2}} \frac{3 α^{2} + 4 α + 3}{α^{2}} x^{2} + 1 N_{2}^{b} = \frac{1}{L^{4}} \frac{1}{α^{2}} x^{5} - \frac{1}{L^{3}} \frac{2 (α + 1)}{α^{2}} x^{4} + \frac{1}{L^{2}} \frac{α^{2} + 4 + 1}{α^{2}} x^{3} - \frac{1}{L} \frac{2 (α + 1)}{α} x^{2} + x N_{3}^{b} = - \frac{1}{L^{5}} \frac{2 (α - 1)}{α^{3} {(α - 1)}^{3}} x^{5} + \frac{1}{L^{4}} \frac{5 α^{2} + 5 α - 4}{α^{3} {(α - 1)}^{3}} x^{4} + \frac{1}{L^{3}} \frac{2 (α^{2} - 5 α + 1)}{α^{3} {(α - 1)}^{3}} + \frac{1}{L^{2}} \frac{5 α - 3}{α^{2} {(α - 1)}^{3}} x^{2} N_{4}^{b} = \frac{1}{L^{4}} \frac{1}{α^{2} {(α - 1)}^{2}} x^{5} - \frac{1}{L^{3}} \frac{α + 2}{α^{2} {(α - 1)}^{2}} x^{4} + \frac{1}{L^{2}} \frac{2 α + 1}{α^{2} {(α - 1)}^{2}} x^{3} - \frac{1}{L} \frac{1}{α {(α - 1)}^{2}} x^{2} N_{5}^{b} = \frac{1}{L^{5}} \frac{2 (2 - α)}{{(α - 1)}^{3}} x^{5} + \frac{1}{L^{4}} \frac{4 α^{2} - 5 α - 5}{{(α - 1)}^{3}} - \frac{1}{L^{3}} \frac{2 α (α^{2} + α - 1)}{{(α - 1)}^{3}} x^{3} + \frac{1}{L^{2}} \frac{α^{2} (3 α - 5)}{{(α - 1)}^{3}} x^{2} N_{6}^{b} = \frac{1}{L^{4}} \frac{2 (2 - α)}{{(α - 1)}^{2}} x^{5} - \frac{1}{L^{3}} \frac{2 α + 1}{{(α - 1)}^{2}} x^{4} + \frac{1}{L^{2}} \frac{α (α + 2)}{{(α - 1)}^{2}} x^{3} - \frac{1}{L} \frac{α^{2}}{{(α - 1)}^{2}} x 2

여기서, 요소내 직교변향 변위는 $v = \sum_{α} N_{α}^{b} \cdot d_{α}$ 으로 절점변위 d = [v₁,θ₁,v₂,θ₂,v₃,θ₃]^T로 부터 산정할수 있다.

2절점 직교방향의 변위 v에 대한 형상함수는 기존의 연구 문헌를 참고할수 있다(Zienkiewicz and Taylor, 2000). 다만 2절점 요소는 낮은 형상함수의 차수로 인하여 전단력이 요소전체에서 동일한 값을 갖는다.

마지막으로 식 (20)의 공간 보간(discretization in space)함수를 쉘요소의 축방향 힘평형 방정식 (13)과 쉘의 휨 변형 방정식 (18)의 Galerkin 수식화에 도입하였다.

(20)

d u = \sum_{i} N_{α}^{a} \cdot T_{α, i} \cdot D_{i,} w^{a} = \sum_{j} N_{α}^{a} \cdot T_{α, i} \cdot D_{j} d v = \sum_{i} N_{α}^{b} \cdot T_{α, i} \cdot D_{i,} w^{b} = \sum_{j} N_{α}^{b} \cdot T_{α, i} \cdot D_{j}

여기서 D는 전체 좌표계에서의 변위 증분이며, $T$ 는 전체 좌표계에서의 변위를 국부 좌표계에서의 변위(u, v)로 변환하는 행렬이다(Zienkiewicz and Taylor, 2000).

가우스 구적법(Gaussian quadrature)을 이용하여 개별 쉘요소에 대한 강성행렬(K)과 불균형 하중행렬(F)을 계산하고, 이를 이용하여 전체 해석의 주변수(D)에 대한 행렬 방정식을 수립하였다. 제시된 유한요소는 Galerkin 수식화 형태로 제시되어 3절점의 요소를 이용한 곡선 모양의 구조체의 모델링이 용이하며, 모델링의 효율성과 정확도을 향상시켰다. 개발된 축대칭 쉘요소는 토사와 암반의 다공질흐름에 대한 THMC해석을 위하여 개발된 Geo-COUS(Geo-COUpled Simulator) 유한요소 프로그램과 결합하였다.

3. 수치해석 예제

3.1 등분포 하중이 작용하는 원형판

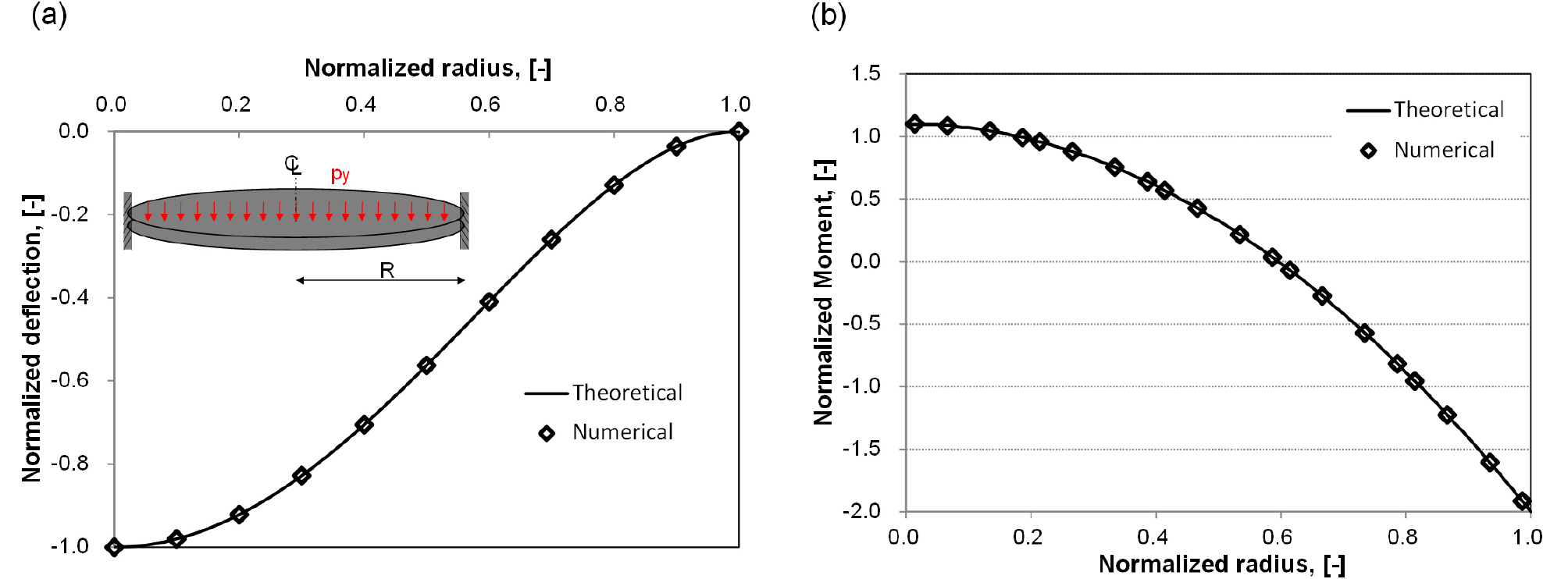
등분포 하중이 작용하는 원형판에 대한 수치해석은 이론식(Timoshenko and Woinowsky-Krieger, 1959)과 비교하여 개발된 쉘요소의 정확성을 판단하기 위하여 사용되었다(Boisse and Coffignal, 1999; PLAXIS, 2018; Raveendranath et al., 1999; Tessler, 1982).

3절점 쉘요소 5개(절점수=21)를 이용하여 끝단 고정상태의 원형판에 대한 수치해석을 수행하였다. Fig. 3에서 수치해석 결과는 원형판의 중심으로 부터 이격거리에 따라 연직방향 침하량과 모멘트가 이론식과 동일함을 확인할수 있다(Fig. 3). 그리고 수치해석은 전단력, 원주방향 축력과 모멘트을 정확하게 산정하였다. 3절점 요소는 고차원 형상함수(식 (19))를 사용하므로, 1개의 요소를 이용하더라도 각 절점에서 침하량과 적분점에서의 부재력은 이론식과 일치하였다.

https://static.apub.kr/journalsite/sites/kgs/2020-036-12/N0990361203/images/kgs_36_12_03_F3.jpg

Fig. 3

Numerical result for the clamped circular plate under uniformly distributed load (a) Normalized of deflection, v/(p_yR⁴/64D^b), (b) Normalized Moment, M_x/(p_yR²/16)

3.2 액체 저장 탱크와 지반의 상호작용

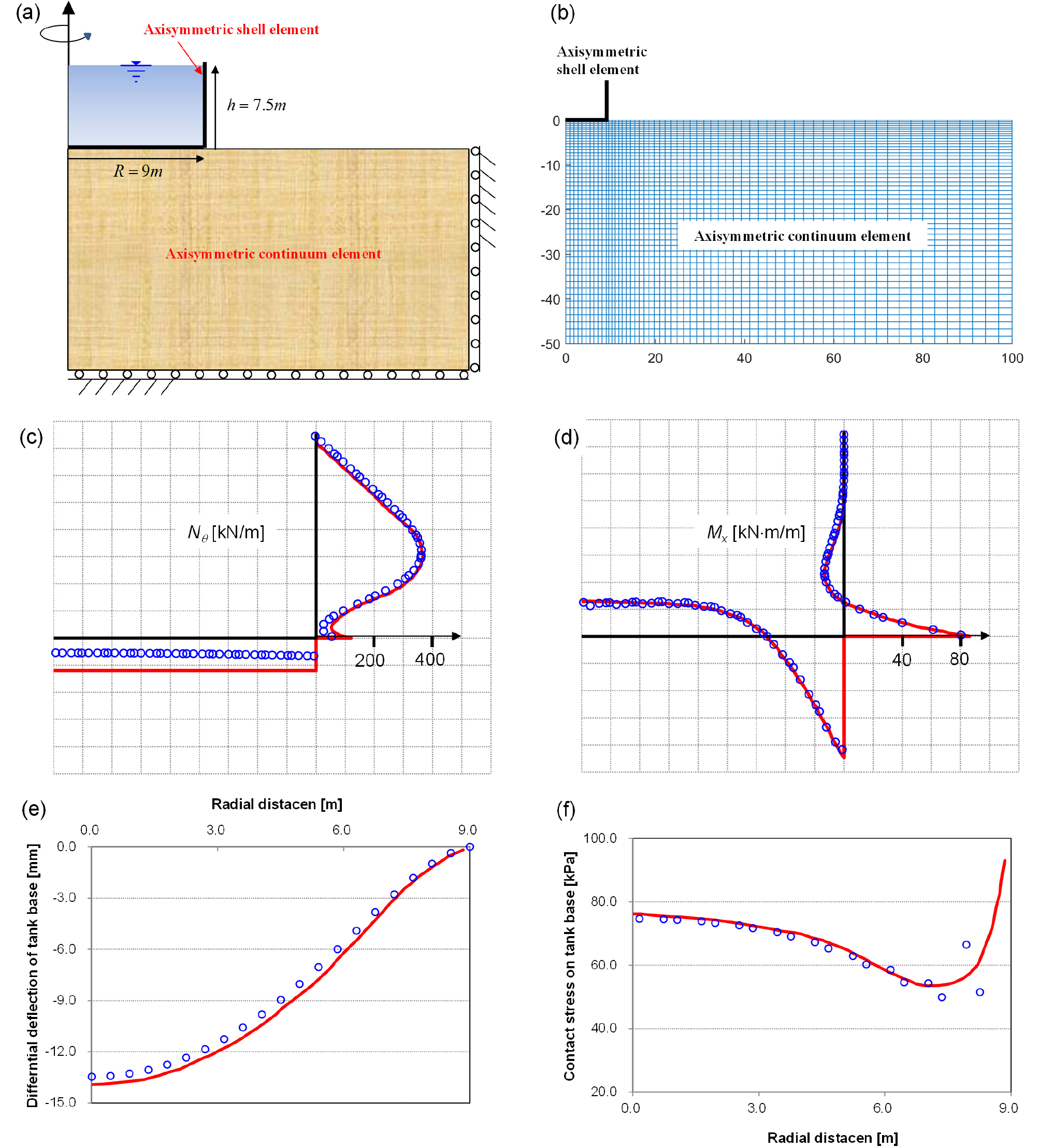
원통형 저장 탱크는 벌크형 액체 저장시설로 널리 사용되며, 특히 에너지나 독성이 높거나 환경에 해로운 액체를 저장하는데 이용되므로 저장 탱크의 거동을 정확하게 예측하는 것이 중요하다(Cheung and Zinkiewicz, 1965; Kukreti and Siddiqi, 1997; Melerski, 1991). 수치 예제는 Booker and Small(1983)이 제시한 저장 탱크의 기하학적 조건과 물성치을 이용하여 해석을 수행하였다(저장 탱크: R=9m, H=7.5m, t=36cm, E=14GPa, 하부지반: E=20MPa, ν=0.4). 저장 탱크는 축대칭 쉘요소(3절점) 20개로 모델링하고, 하부지반은 2차원 축대칭 연속체 요소(8절점) 3000개를 이용하였다(Fig. 4(a), 4(b)). 저장탱크 하부는 동일한 크기의 쉘요소와 지반 연속체 요소를 사용하였다.

Fig. 4(c)에서 탱크 내의 유체 압력이 바닥에서 1/3 높이 부근의 측벽에 큰 인장력을 유발함을 알수 있다. 이론식(Booker and Small, 1983)은 저장 시설 하부지반의 연직방향 저항력만을 고려하고 수평방향의 저항을 고려하지 않아, 탱크 측벽에 작용하는 유체 압력에 의하여 탱크의 바닥에 일정한 크기의 인장력(N_θ=120kPa/m)이 발생하는 것으로 과대 평가하였다. 하지만, 수치해석에 의한 결과는 탱크 하부 지반의 수평방향의 저항에 의하여 변위가 억제되어 이론식보다 작은 원주방향 축하중이 발생하는 것으로 나타났다. Fig. 4(d)의 최대 축방향 모멘트(M_x)는 저장 탱크의 벽과 바닥의 모서리에서 발생하고, 탱크 바닥의 중심부근에서도 큰 모멘트가 유발됨을 알수 있다.

Fig. 4(e)는 탱크의 모서리에서의 연직침하량을 기준으로 탱크 바닥의 부등 침하량을 보여주고 있다. 탱크의 중심부에서는 액체의 자중으로 (+)을 곡률을 나타내지만 벽체에 가까워질수록 벽체에 작용하는 액체의 압력에 의하여 (-)의 곡률이 발생하였다. 부등 침하량에 대한 이론식의 결과가 수치해석보다 큰 것은 이론식에서 지반의 수평방향의 저항력을 고려하지 않았기 때문이다. Fig. 4(f)는 탱크의 바닥에 작용하는 지반의 접촉응력을 나타내며, 탱크의 중심에서 멀어질수록 벽체에 작용하는 유체의 수평방향 압력에 의하여 접촉압력이 감소함을 알수 있다. 탄성지반위에 놓인 저장시설의 모서리에서 접촉응력은 응력집중으로 무한대로 발산하지만, 수치해석에서는 요소내부의 적분점에서 연직응력을 계산하므로 이론적인 값보다 작게 나타난다. 또한, 연속체 유한요소법에서 응력은 2차 변수이므로, 응력 집중구간에서 응력을 정확하게 산정하기 위해서는 메쉬를 조밀하게 작성하여야 한다.

https://static.apub.kr/journalsite/sites/kgs/2020-036-12/N0990361203/images/kgs_36_12_03_F4.jpg

Fig. 4

Numerical results of water-filled tanks with open tops: (a) Model configuration of water-storage tank, (b) Finite element mesh, (c) Circumferential axial force N_θ, (d) Radial moment M_x, (e) Differential deflection of the base, (f) contact stress between tank base and subsoil

마지막으로 액체 저장시설에서 열-역학적 연계해석을 수행하기 위해서는 축대칭 쉘요소에 대한 에너지 평형방정식이 필요하다(Shin et al., 2009). 우선 쉘의 전체 변형률은 역학적 변형률과 열적 변형률의 합으로 산정되므로, 축대칭 쉘의 변형률과 변위의 관계를 다음과 같이 수정하여야 한다.

(21)

ε_{x} = \frac{d u}{d x} - α_{T} \cdot d T, ε_{θ} = \frac{u \cdot \cos (α) - v \cdot \sin (α)}{r} - α_{T} \cdot d T

여기서, α_T는 쉘요소의 선형 열수축계수(linear thermal contractive coefficient)이다.

그리고 축대칭 쉘요소에 대한 에너지 평형 방정식은 다음과 같이 정리할수 있다.

(22)

ρ_{s} C_{s} h \frac{\partial T}{\partial t} r - λ_{s} h \frac{\partial}{\partial x} (r \cdot \frac{\partial T}{\partial x}) = 0

여기서, ρ_s, C_s, λ_s는 쉘요소의 밀도, 열용량, 열전도도를 의미한다. 쉘요소의 축방향 힘평형 방정식에 대한 Galerkin 수식화과 동일한 방법으로 에너지 평형 방정식에 대한 수식화를 수행할수 있다.

4. 결 론

지반공학에서 구조물을 포함하는 수치해석은 일반적인 토목 구조물 뿐만 아니라 원자력 구조물 등 다양한 분야에서 수행되고 있다. 특히 축대칭 조건에 축대칭 하중이 작용하는 경우에는 3차원 해석을 2차원 축대칭 해석으로 변환함으로써 수치해석의 효율성을 높일수 있다. 지반에 대한 축대칭 연속체 유한요소는 2차원 평면변형률 요소로부터 적분점에 대한 가중치만을 조정하여 간단히 수식화의 수정이 가능하지만, 축대칭 쉘요소는 일반적인 2차원이나 3차원 요소와는 다른 지배방정식의 수식화가 필요하다. 본 논문에서는 축대칭 쉘에 대한 힘과 모멘트 평형 방정식들을 유도하고 3절점 축대칭 쉘요소에 대한 Galerkin 수식화를 제시하였다.

지배방정식은 전단변형을 무시하고 휨 변형만을 고려하는 얇은 쉘에 대한 Kirchhoff 이론을 바탕으로 유도하였다. 축대칭 쉘요소의 축방향과 직교방향에 대한 힘평형 방정식을 유도하고, 쉘요소의 면에 대한 모멘트 평형방정식을 정리하였다. 그리고 모멘트 평형방정식과 직교방향 힘평형 방정식을 결합하여 쉘요소의 휨에 대한 지배 방정식으로 정리하였다. 축방향 변형에 대한 지배방정식은 C₀ 연속성만을 만족하는 등매개변수 형상함수를 이용하여 Galerkin 수식화를 수행하고, 휨에 대한 지배방정식은 C₁ 연속성을 만족하는 고차의 형상함수를 이용하여 수식화를 수행하였다.

개발된 축대칭 쉘요소는 등분포 하중이 작용하는 원형판에 대하여 이론식과의 정확성과 수치적인 안정성을 확인하였다. 그리고 지반과 구조물에 대한 상호작용에 대한 예제 해석으로 액체 저장 탱크와 지반에 대한 예제 해석을 수행하였다. 기존의 이론식에서 저장 시설 하부지반의 연직방향 저항력만을 고려하고, 수평방향의 저항을 고려하지 않아, 탱크바닥의 수평변위를 과다하게 산정함을 알수 있었다. 그리고 지반과 구조물의 열-역학적 상호작용 작용을 해석하기 위한 축대칭 쉘요소에 대한 에너지 평형방정식을 제시하였다.

Acknowledgements

본 연구는 한국연구재단 개인연구지원사업(NRF-2019R1A2C200441912)과 학문후속세대양성사업(NRF-2019R1A6A3A1309618812)의 연구비 지원으로 수행되었으며, 이에 깊은 감사를 드립니다.

References

Boisse, P. and Coffignal, G. (1999), "Error through the Constitutive Relation for Beam and C0 Plate Finite Elements: Static and Vibration Analyses", Computer Methods in Applied Mechanics and Engineering, Vol.176, No.1-4, pp.81-109. 10.1016/S0045-7825(98)00331-4

Booker, J.R. and Small, J.C. (1983), "The Analysis of Liquid Storage Tanks on Deep Elastic Foundations", Int. J. Numer. Anal. Meth. Geomech., 7, pp.187-207. 10.1002/nag.1610070205

Cheung, Y.K. and Zinkiewicz, O.C. (1965), "Plates and Tanks on Elastic Foundations - An Application of Finite Element Method", International Journal of Solids and Structures, Vol.1, No.4, pp.451-461. 10.1016/0020-7683(65)90008-9

Flügge, W. (1973), Stresses in shells, Springer, p.526. 10.1007/978-3-642-88291-3

Grafton, P.E. and Strome, D.R. (1963), "Analysis of Axisymmetrical Shells by the Direct Stiffness Method", AIAA Journal, Vol.1, No.10, pp.2342-2347. 10.2514/3.2064

Jones, R.E. and Strome, D.R. (1966), "Direct Stiffness Method Analysis of Shells of Revolution Utilizing Curved Elements", AIAA Journal, 4(9), pp.1519-1525. 10.2514/3.3729

Kukreti, A.R. and Siddiqi, Z.A. (1997), "Analysis of Fluid Storage Tanks Including Foundation-superstructure Interaction Using Differential Quadrature Method", Applied Mathematical Modelling, Vol.21, No.4, pp.193-205. 10.1016/S0307-904X(97)00007-3

Melerski, E.S. (1991), "Simple Elastic Analysis of Axisymmetric Cylindrical Storage Tanks", Journal of Structural Engineering, Vol.117, No.11, pp.3239-3260. 10.1061/(ASCE)0733-9445(1991)117:11(3239)

PLAXIS (2018), "Bending of axisymmetric plates".

Prathap, G. and Ramesh, B.C. (1986), "A Field Consistent Three-noded Quadratic Curved Axisymmetric Shell Element", 23, pp.711-724. 10.1002/nme.1620230413

Raveendranath, P., Singh, G., and Pradhan, B. (1999), "A Two-node Curved Axisymmetric Shell Element based on Coupled Displacement Field", Int. J. Numer. Methods Eng., 45, pp.921-935. 10.1002/(SICI)1097-0207(19990710)45:7<921::AID-NME618>3.0.CO;2-I

Shin, E.C., Kang, J.G., and Park, J.J. (2009), "Thermal Stability in Underground Structure with Ground Freezing", J. of the Korean Geotechnical Society, Vol.25, No.3, pp.65-74.

Tessler, A. (1982), "An Efficient, Conforming Axisymmetric Shell Element Including Transverse Shear and Rotary Inertia", Computers & Structures, 15, pp.567-574. 10.1016/0045-7949(82)90008-6

Timoshenko, S. and Woinowsky-Krieger, S. (1959), Theory of plates and shells, McGraw-Hill, p.580.

Zienkiewicz, O.C. and Taylor, R.L. (2000), The Finite Element Method: Solid mechanics, Butterworth-Heinemann, p.459.

Journal of the Korean Geotechnical Society ISSN:1229-2427(Print) 2288-646X(Online) 한국지반공학회 논문집

Preview

Numerical Formulation of Axisymmetric Shell Element and Its Application to Geotechnical Problems

ABSTRACT

MAIN

Fig. 1

(a) Geometric configuration of the shell segment, (b) Force equilibrium of local axial direction (x) on the top view of Figure a, (c) Force equilibrium of local tangential direction (y) on the front view, (d) Moment equilibrium on the shell surface on the top view

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

Fig. 2

Geometry and node numbering in axisymmetric shell element with 3-nodes (Length to mid-node, Lα=α·L)

(19)

(20)

Fig. 3

Numerical result for the clamped circular plate under uniformly distributed load (a) Normalized of deflection, v/(pyR4/64Db), (b) Normalized Moment, Mx/(pyR2/16)

Fig. 4

Numerical results of water-filled tanks with open tops: (a) Model configuration of water-storage tank, (b) Finite element mesh, (c) Circumferential axial force Nθ, (d) Radial moment Mx, (e) Differential deflection of the base, (f) contact stress between tank base and subsoil

(21)

(22)

Acknowledgements

References

Geometry and node numbering in axisymmetric shell element with 3-nodes (Length to mid-node, L_α=α·L)

Numerical result for the clamped circular plate under uniformly distributed load (a) Normalized of deflection, v/(p_yR⁴/64D^b), (b) Normalized Moment, M_x/(p_yR²/16)

Numerical results of water-filled tanks with open tops: (a) Model configuration of water-storage tank, (b) Finite element mesh, (c) Circumferential axial force N_θ, (d) Radial moment M_x, (e) Differential deflection of the base, (f) contact stress between tank base and subsoil