1. 서 론
지진 시 지진파는 지반을 통과하면서 지반의 특성에 따라 증폭현상이 발생하며 이를 보다 정확히 예측하는 것은 내진설계를 위하여 필수적으로 수행되어야 한다. 가장 널리 사용하는 부지응답해석 기법은 주파수영역에서 수행하는 등가선형해석기법과 시간영역에서 수행하는 비선형해석기법이 있다. 비선형해석기법은 직접 수치적분방법을 사용하여 각 시간단계마다 강성행렬을 업데이트하므로 지반의 거동을 보다 정확하게 모사할 수 있다.
비선형 부지 증폭 효과는 일반적으로 대상 부지에 대한 1차원 부지응답해석을 수행하여 산정할 수 있다. 지반의 비선형 거동을 모델링하기 위해서는 공진주/비틂 전단 시험에서 측정된 동적곡선(Dynamic curve)을 사용한다. 하지만 공진주/비틂 전단 시험기의 용량 제한으로 인하여 0.1% 이하의 전단변형률만 재하 가능하며, 그 이상의 대변형에 대해서는 외삽에 의한 추정치를 사용하므로 신뢰도가 크게 감소하는 것으로 알려져 있다. 특히 큰 변형이 발생하는 경우, 전단응력은 전단강도에 수렴해야 하지만 정규화된 전단탄성계수(G/Gmax) 감소곡선은 전단강도를 크게 과소/과대평가할 수 있으므로 이를 적절히 보정해야 한다(Groholski et al., 2016). 기존 연구에서 1차원 부지응답해석 수행 시 전단강도 보정을 적용하기 위한 다양한 모델이 제안되었다. Yee et al.(2013)은 큰 전단변형률 범위에서 전단강도를 조정하기 위해 두 개의 쌍곡선 함수를 사용하였다. Shi와 Asimaki(2017)는 목표 전단강도에 일치하도록 가중치 함수를 적용한 하이브리드 쌍곡선 모델을 개발하였다. Groholski et al.(2015)은 목표 전단강도 보정이 가능한 2차 쌍곡선(general quadratic hyperbolic, GQ/H) 함수로 표현되는 구성 모델을 제안하였으며, 이 기능은 1차원 부지응답해석 프로그램인 DEEPSOIL(Hashash et al., 2020)에 탑재되어 있다.
기존 연구에 따르면 지진 위험도가 높고 기반암까지의 심도가 깊은 지반에 대해 부지응답해석 시 전단강도의 보정이 중요한 것으로 알려져 있다(Yee et al., 2013; Groholski et al., 2015). Aaqib et al.(2018)은 얕은 기반암 심도와 지진 위험이 높지 않은 지역에서의 전단강도 보정의 필요성을 논의한 바 있다. 하지만 부지의 고유주기(TG)와 같은 부지 매개변수 혹은 입력지진파의 평균주기(Tm)와 같은 입력지진파의 특성이 전단강도 보정에 미치는 영향에 대해서는 아직 관련 연구가 수행되지 않았다.
본 연구의 목적은 국내 내륙 지반의 일반적인 특성인 얕은 기반암 조건과 지진 위험도가 상대적으로 낮은 지역에 대한 전단강도 보정의 필요성을 평가하고, TG와 Tm이 전단강도 보정에 미치는 영향을 분석하는 것이다. 이를 위해 국내에서 측정된 다양한 다운홀 시험 자료를 사용하여 Modified Kondner-Zelasko(MKZ) 모델(Matasovic, 1993)과 GQ/H 모델에 의한 비선형 부지응답해석을 수행하였다. 각각의 모델에 의해 산정된 유효최대지반가속도(Effective peak ground acceleration, EPGA)와 최대전단변형률은 TG와 Tm의 함수로 상세히 비교하여 그 영향을 평가하였다.
2. 지반강도 보정 구성모델
DEEPSOIL에는 MKZ 모델과 GQ/H 모델 등 구속압에 의존적인 쌍곡선 함수로 표현 가능한 비선형 지반구성모델들이 탑재되어 있다. MKZ 모델에서 전단응력과 전단변형률 간의 쌍곡선형 관계는 다음과 같이 정의된다(식 (1)).
여기서, τ는 전단응력, γ는 전단변형률, G0는 초기 전단탄성계수이며 β와 s 그리고 γr은 각각 모델의 매개변수이다. DEEPSOIL에서 γr은 식 (2)와 같이 구속압에 의해 결정된다(Hashash와 Park, 2001).
여기서, σv’은 연직 유효응력, σref는 기준 응력이며, γr이 기준 전단변형률과 같을 때의 연직 유효응력 값을 기준 응력 값으로 산정한다.
MKZ 모델은 미소변형률 범위에서의 거동은 적절히 모사할 수 있지만 전단변형률이 증가함에 따라 비현실적인 전단응력 변화가 발생하기 때문에 지반의 거동이 제대로 제어할 수 없게 된다. 이는 대변형 구간에서 전단강도의 과소/과대 평가를 야기할 수 있다.
GQ/H 모델은 미소변형률 영역에서 비선형 지반 거동을 모사하면서 동시에 파괴 시 전단강도를 정의할 수 있다. 전단응력과 전단변형률 간의 관계는 다음과 같다(식 (3)).
여기서, τmax는 사용자에 의해 정의되는 파괴 시 전단강도이며, γr은 γr = τmax/G0로 계산되는 기준 전단변형률이다. θτ는 곡선적합(curve fitting) 매개변수이며 다음과 같이 정의된다(식 (4)).
여기서, θ1 ~ θ5는 모두 모형의 매개변수이다.
Masing 법칙에 기반한 역재하-재재하 응력-변형률 곡선에 의한 이력 감쇠 거동 산정은 큰 전단변형률에서의 감쇠를 과대평가하는 것으로 알려져 있다. 보다 정확한 목표 감쇠곡선과의 일치를 위해 DEEPSOIL에 내장된 Non-Masing 모델은 Phillips와 Hashash(2009)에 의해 개발되었으며 목표 동적곡선을 동시에 맞추는 조정 절차(modulus reduction and damping curve fitting procedure, MRDF) 기법을 사용한다. MRDF 감소 계수 F는 다음과 같이 정의된다(식 (5)).
여기서, γmax는 주어진 시간에서 최대 전단변형률, G(γmax)는 γmax에서의 할선전단탄성계수이며 P1, P2, P3는 매개변수이다. GQ/H 모델의 역재하-재재하 식은 아래와 같다(식 (6)).
여기서, γrev과 τrev는 전단응력이 역전되는 때의 전단변형률과 전단응력이며, Gγmax는 뼈대곡선(backbone curve)에서 γmax일 때의 할선전단탄성계수이다.
3. 1차원 부지응답해석
3.1 지반주상도
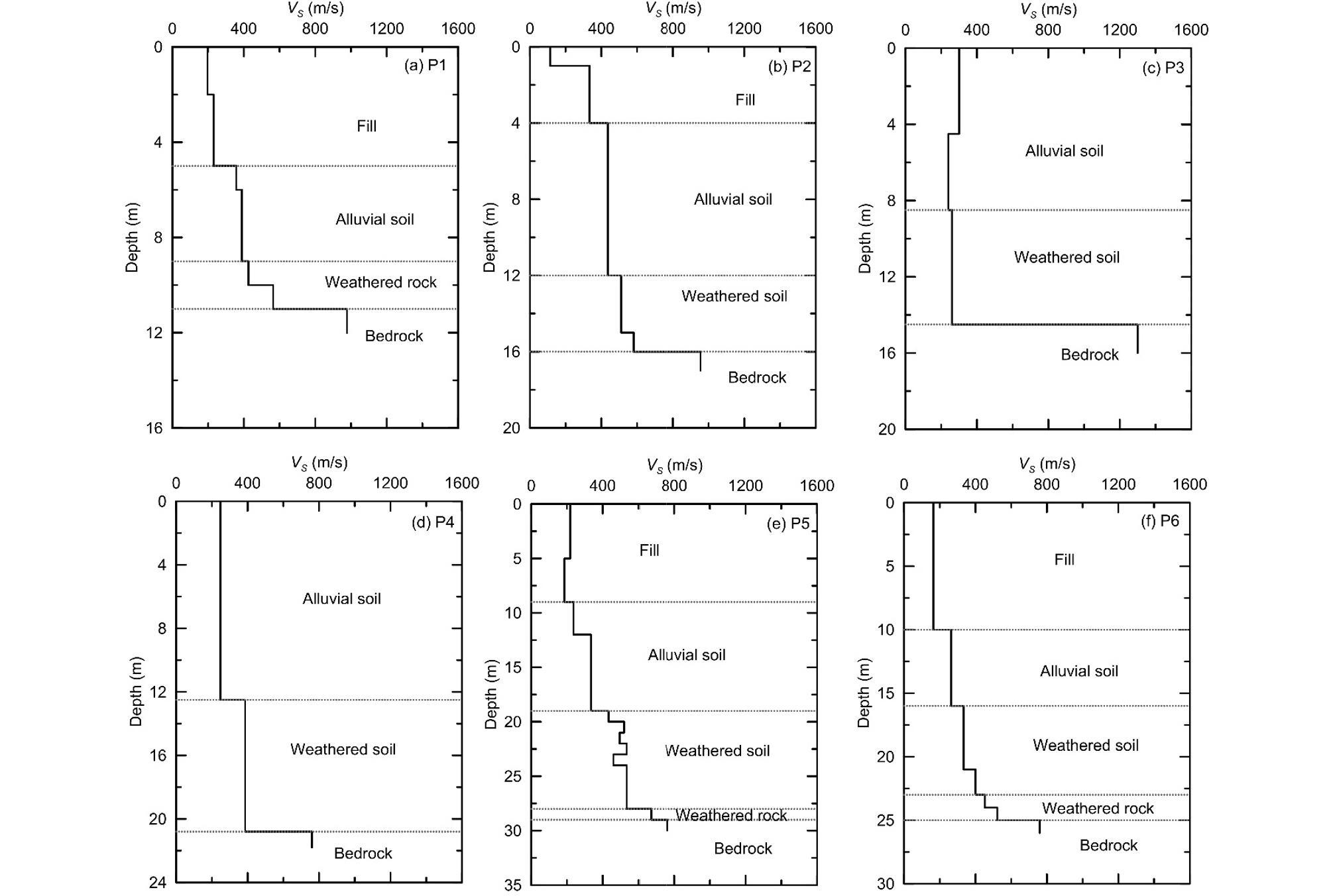
본 연구에서는 국내에서 측정한 6개소의 다운홀 시험 자료를 사용하였다. 선정된 자료에서 TG의 범위는 0.15~0.43sec이며, 기반암의 깊이(H)는 11~29m이다. 대부분의 부지는 매립층, 충적토층, 풍화토층 그리고 풍화암층으로 구성되어 있다. 기반암은 내진설계일반(KDS 17 10 00: 2018)(MOLIT, 2018)에 부합하도록 전단파속도(Shear wave velocity, Vs)가 760m/s를 초과하는 지층으로 정의하였다. 본 연구에서 사용한 자료에서 기반암의 Vs 범위는 760~1,280m/s이다. 선정된 자료는 내진설계일반의 지반 분류에 따라 S2와 S4 지반 등급이 각각 3개이다. 선정된 부지의 특성은 Table 1에 요약되어 있으며, Vs 주상도에 지층정보를 함께 표기하여 Fig. 1에 도시하였다. GQ/H 모델의 전단강도를 정의하기 위해 Mohr-Coulomb 모델을 사용하였다. 대상 부지에서 마찰각 측정 자료가 없으므로 다음과 같은 절차로 Vs로부터 마찰각을 산정하였다. 먼저 Sun et al.(2013)이 제안한 Vs와 표준관입시험 관입치(N60)간의 경험적 상관관계를 나타내는 식 (7)을 이용하여 N60을 산정한다.
Table 1.
Summary of selected profiles
| No. | H (m) | TG (s) | Vs,soil (m/s) | KDS site class |
| P1 | 11.0 | 0.15 | 293 | S2 |
| P2 | 16.0 | 0.18 | 365 | S2 |
| P3 | 14.5 | 0.22 | 265 | S2 |
| P4 | 20.8 | 0.29 | 289 | S4 |
| P5 | 29.0 | 0.39 | 298 | S4 |
| P6 | 25.0 | 0.43 | 232 | S4 |
Wolff(1989)가 제시한 N60와 마찰각의 상관관계를 나타내는 식 (8)을 사용하여 대상 부지에서의 마찰각을 산정하였다.
3.2 입력지진파
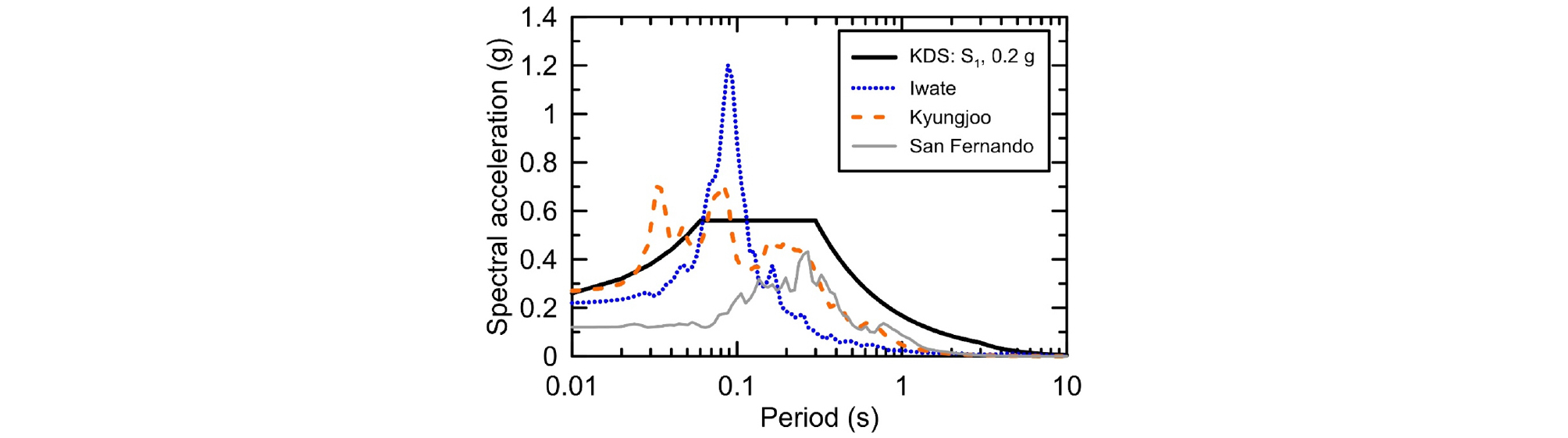
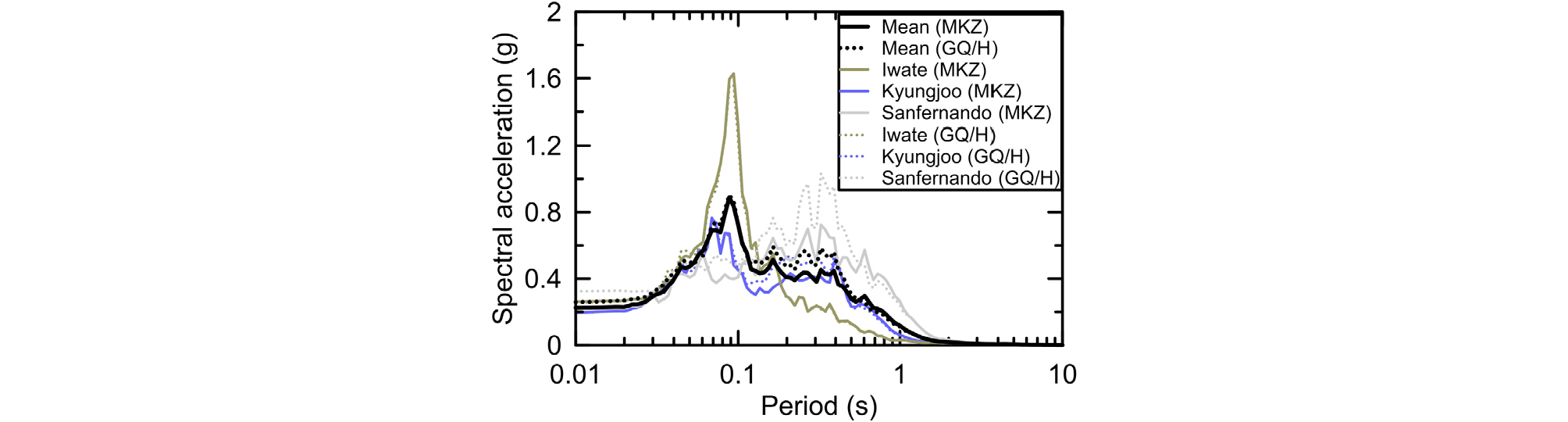
본 연구에 사용된 입력지진파는 총 3개이며, 이 중 2개는 NGA-West 2 데이터베이스(PEER ground motion database, 2013)에서 선정하였으며, 1개는 2016년 경주 지진 시 한국지질자원연구원 운영 계측소에서 기록된 지진파(KIGAM, 2016)이다. 선정된 입력지진파의 가속도 응답스펙트럼은 Fig. 2에 도시하였다. 전단강도 보정에 대한 입력지진파의 영향을 살펴보기 위해 다양한 Tm을 갖는 지진기록을 선정하였다. 기반암에 재하하는 입력지진파는 S1 지반으로 추정되는 조건의 계측자료만을 선정하였으며 최대지반가속도(Peak ground acceleration, PGA)는 0.2g로 선형 조정하였다. 선정된 입력지진파의 상세는 Table 2에 정리하였다.
Table 2.
Details of input ground motions
3.3 해석 절차
본 연구에서는 DEEPSOIL을 사용하여 1차원 비선형 부지응답해석을 수행하였다. 비선형해석을 위해 지반의 구성모델은 MKZ 모델과 GQ/H 모델을 함께 사용하였다. 목표 동적곡선은 Darendeli(2001)가 제안한 동적곡선을 선정하였고, 역재하-재재하 시 응력-변형률 거동은 Non-Masing 법칙을 따르도록 적용하였다. 또한, 목표 동적곡선을 동시에 맞추기 위해 MRDF 기법을 적용하여 비선형 곡선과 일치하도록 하였다(Phillips and Hashash, 2009). 미소변형률 영역의 감쇠는 Kwok et al.(2007)이 제안한 1차, 5차 모드로부터 계산된 Rayleigh 감쇠 계수를 산정하여 적용하였다.
4. 분석 및 고찰
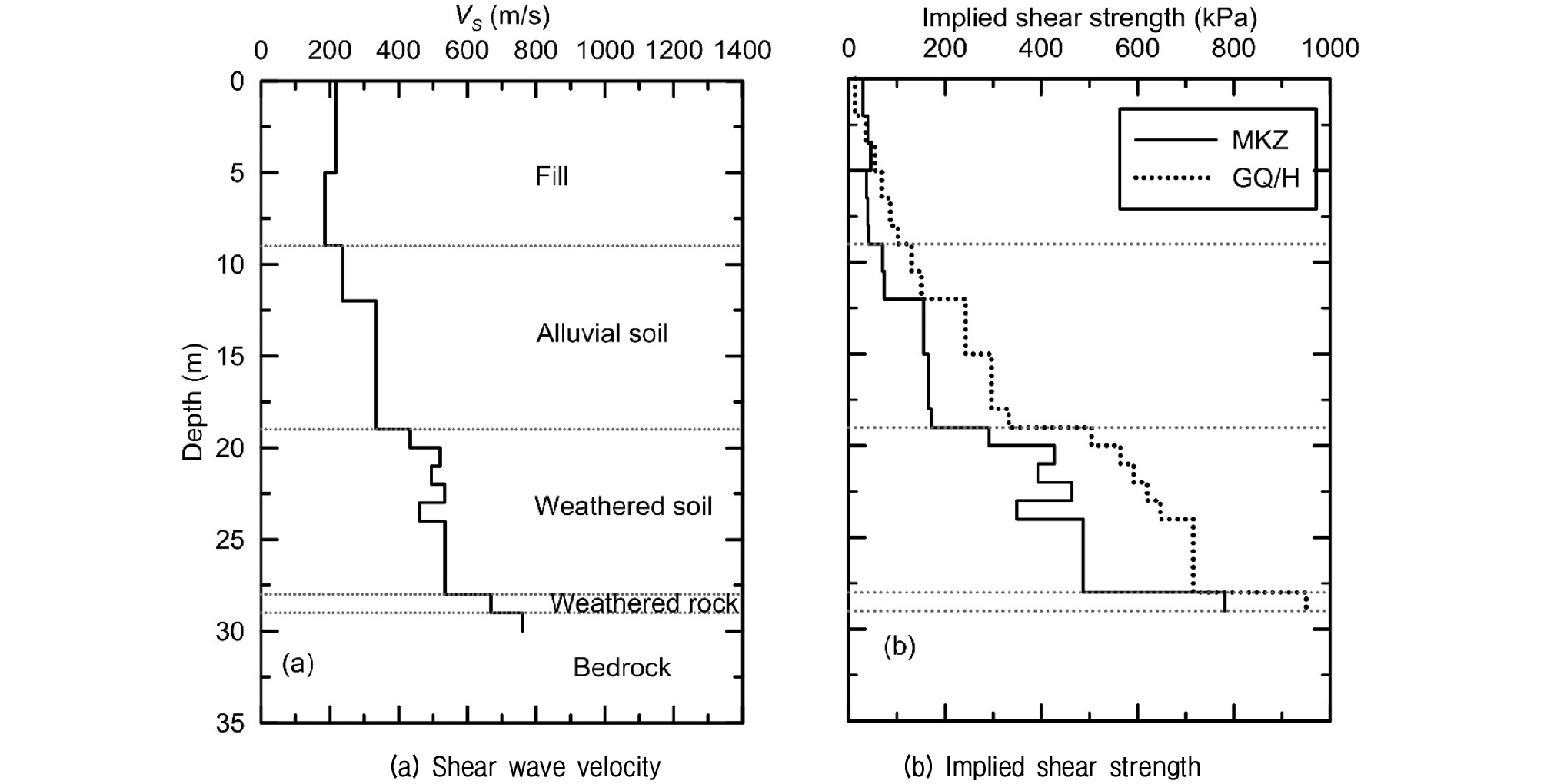
해석 결과의 비교를 위해 6개 부지 중에서 TG가 0.39sec, 토층평균전단파속도(Vs,soil)가 298m/s인 P5 부지를 대표로 선정하였다. Vs와 적용된 전단강도(implied shear strength) 주상도를 Fig. 3에 각각 도시하였다. 적용된 전단강도의 경우 4m 이상의 심도에서 GQ/H 모델의 결과가 MKZ 모델의 결과보다 크게 나타남을 알 수 있다. 나머지 5개 부지의 결과도 동일한 경향을 나타내며 중복을 피하기 위해 나머지 부지의 결과 비교는 생략하였다.
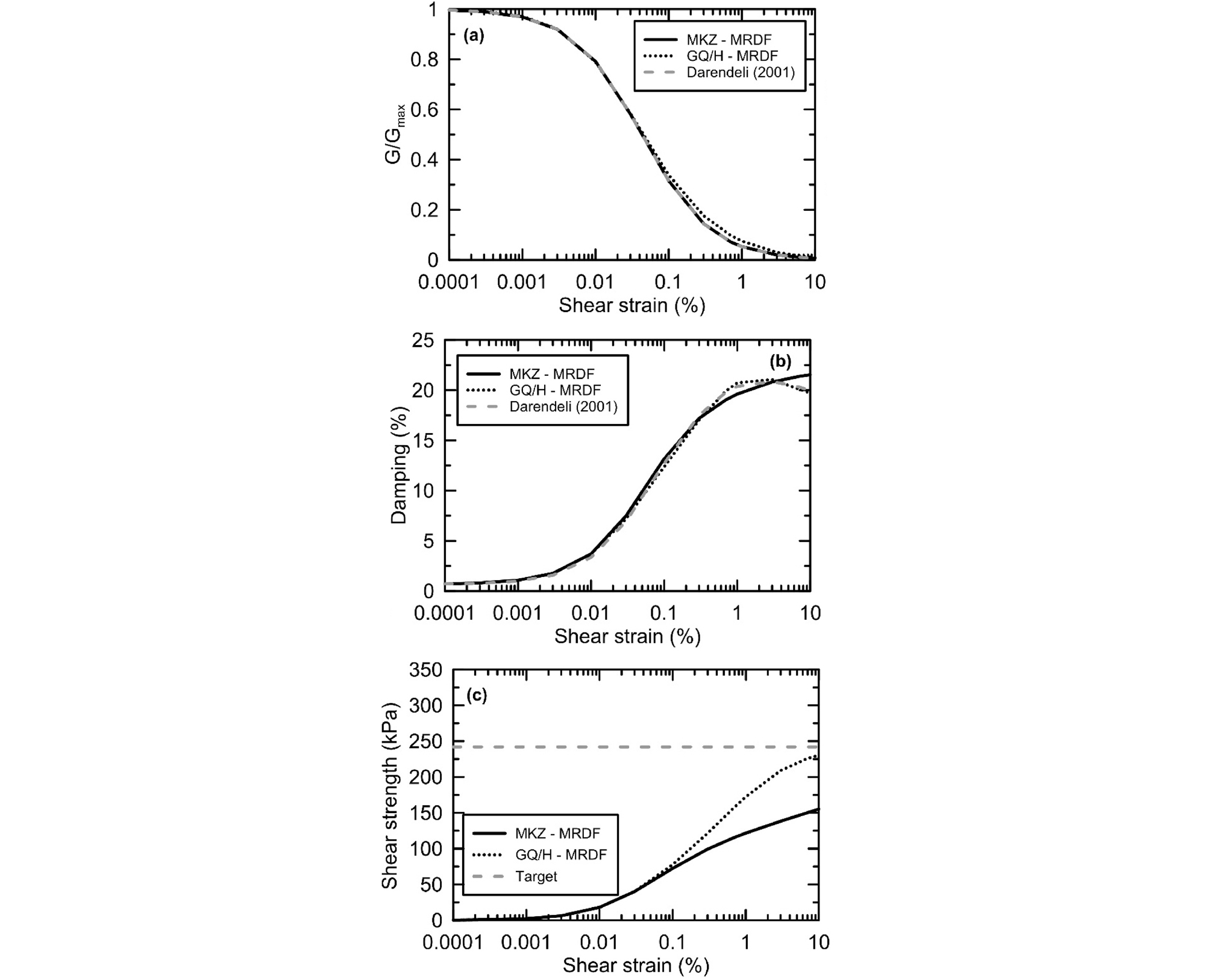
Fig. 4에서는 심도 13m에서 MKZ 모델과 GQ/H 모델에 의해 산정된 G/Gmax, 감쇠비, 전단강도를 전단변형률의 변화에 따라 도시하였다. Fig. 4c에서 볼 수 있듯이 GQ/H 모델에 비해 MKZ 모델은 전단강도를 과소산정하며, 전반적으로 GQ/H 모델의 결과가 목표 비선형 곡선인 Darendeli(2001)의 곡선과 보다 잘 일치하는 것을 확인할 수 있다.
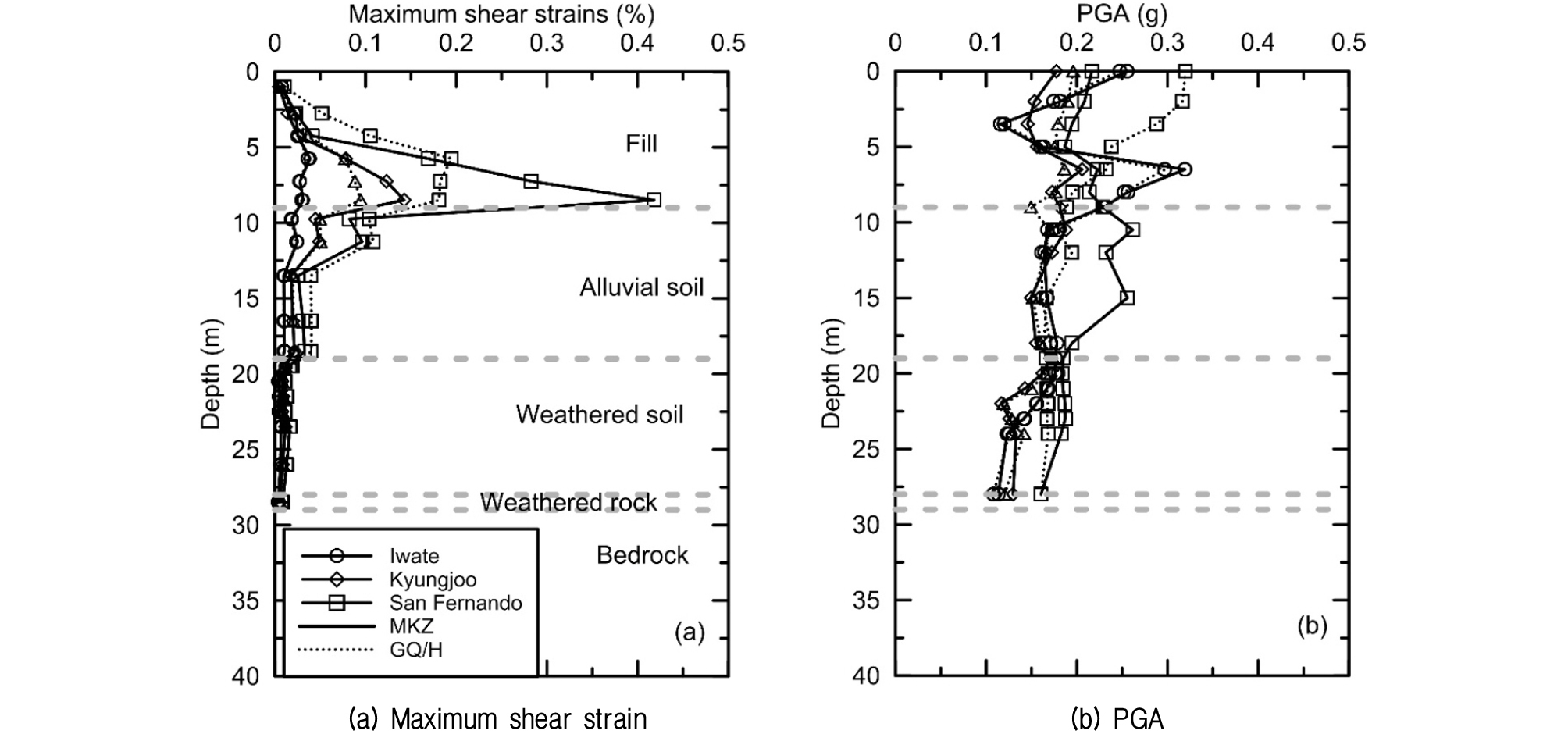
P5 부지의 결과 중 지표면에서의 가속도 응답스펙트럼을 비교하여 Fig. 5에 도시하였다. 가속도 응답스펙트럼의 경우, 주기 0.1~0.5sec 구간에서는 GQ/H 모델의 평균이 MKZ 모델의 평균보다 크게 나타났다. 최대전단변형률 및 PGA 주상도는 Fig. 6에 도시되어 있다. GQ/H 모델에 의한 최대전단변형률은 0.2%인데 비해 MKZ 모델은 0.42%의 결과를 나타낸다. 모든 입력지진파 중 최대전단변형률이 발생하는 경우를 살펴보면, GQ/H 모델의 경우 심도 6m에서 최대전단변형률이 나타나며, MKZ 모델의 경우 9m 깊이에서 발생한다. MKZ 모델의 경우, Vs,soil가 역전되는 매립층에서 상대적으로 크게 발생하며 매립층과 충적토층의 경계 바로 위에서 최대전단변형률이 발생한다. 매립층 내에서 큰 전단변형률이 발생하며, GQ/H 모델의 결과보다 약 2배 정도 크게 나타났다. 또한, 큰 전단변형은 지표면의 PGA에도 영향을 미치며, GQ/H 모델의 PGA가 MKZ 모델의 PGA보다 약 1.5배 크게 나타났다. MKZ 모델의 경우, 매립층과 충적토층 경계에서의 과도한 에너지 소산에 의해 매립층에서 PGA의 명확한 감소가 발생한다. 이와 같은 결과는 MKZ 모델을 사용한 모든 입력지진파에서 확인할 수 있다. 그에 반해 GQ/H 모델의 경우 Iwate 지진파를 제외한 입력지진파들에 대해 지표면으로 갈수록 PGA가 점차 증가하는 것을 확인할 수 있다.
전단강도 보정에 대한 TG와 Tm의 영향을 파악하기 위해 MKZ와 GQ/H 모델에서 산정된 각각의 EPGA 및 최대전단변형률의 비를 분석하였다. EPGA는 식 (9)와 같이 주기 0.1~0.5sec 구간에서 스펙트럴 가속도의 평균을 2.5로 나눈 것과 같다(Kramer, 1996).
여기서, 는 지표면에서의 스펙트럴 가속도이다. Tm은 Fourier 진폭 스펙트럼으로부터 Rathje et al.(2004)이 제안한 방법에 의해 계산되었다.
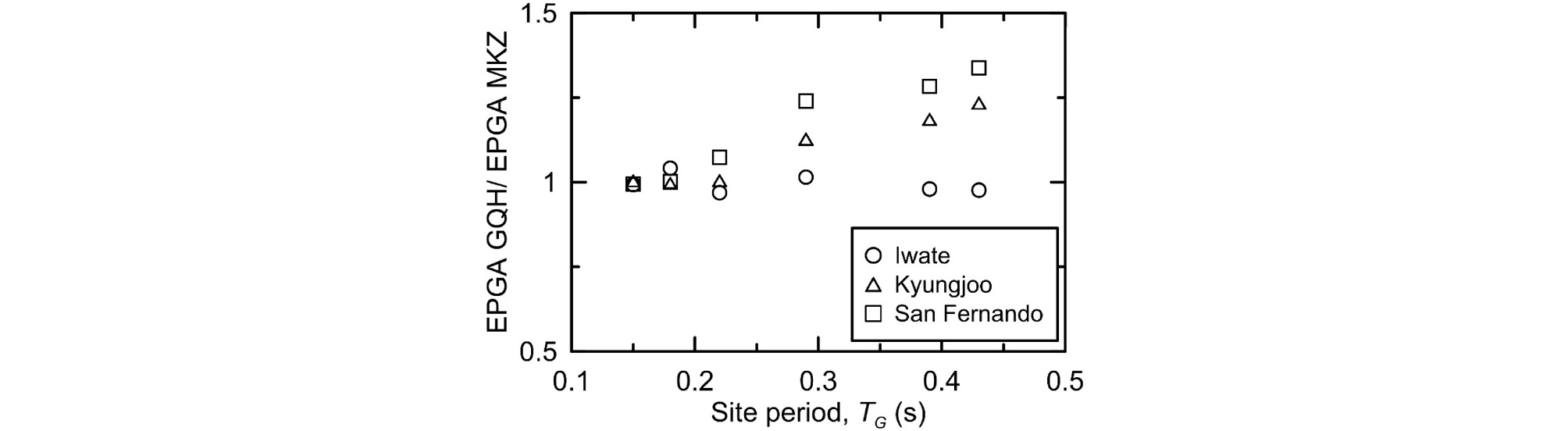
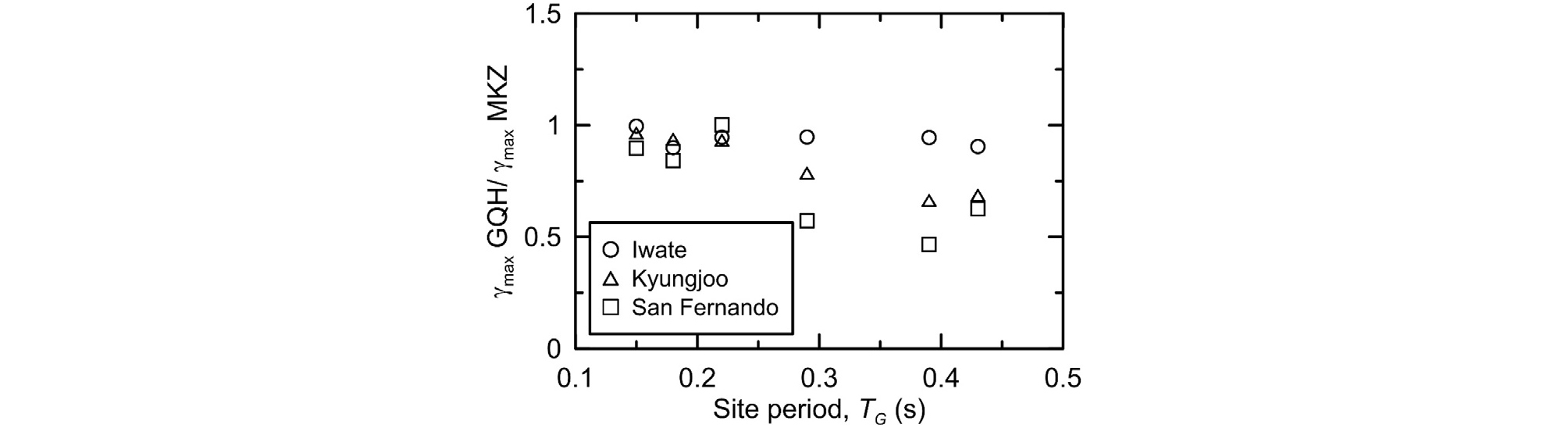
먼저 부지증폭 효과를 살펴보기 위해, 두 모델에 의한 EPGA의 비와 TG 간의 관계를 Fig. 7에 도시하였다. 연약지반일수록 전단강도 보정이 더욱 필요함을 알 수 있다. TG의 증가에 따라 EPGA 비 역시 증가하며, 본 연구에서 사용한 가장 연약한 지반의 경우 EPGA 비가 1.33까지 나타났다. 지반 내에서 Vs의 역전이 발생한다는 것 또한 전단강도 보정이 중요함을 의미한다. Fig. 1에서 P5 부지의 경우 심도가 증가함에 따라 Vs가 감소하는 구간이 존재하며 이로 인해 EPGA 비가 증가한다. Iwate 지진파의 경우 TG의 영향을 거의 받지 않으며, 경주 지진파, San Fernando 지진파로 갈수록 EPGA 비가 커지는 것을 확인할 수 있다. 이는 Iwate 지진파의 Tm이 상대적으로 작아 영향을 받지 않는 것으로 판단된다. Fig. 8에서는 최대전단변형률 비와 TG 간의 관계를 살펴볼 수 있다. 연약지반일수록 최대전단변형률 비는 감소하는데, MKZ 모델의 결과가 상대적으로 큰 전단변형률을 나타내어 그 비율은 0.47까지 감소한다. P1, P2 부지와 같이 TG가 0.2sec 미만인 부지에서는 전단강도 보정의 영향은 무시할 수 있다고 판단된다. EPGA 비의 경향과 유사하게 Iwate 지진파는 큰 변화를 보이지 않으며, San Fernando 지진파에서 최대전단변형률 비가 가장 작게 나타났다.
전단강도 보정이 지반 증폭 특성에 미치는 영향도 분석하였다. 5% 감쇠비를 적용한 가속도 응답스펙트럼에 대해 지표면과 입력지진파의 스펙트럼 비를 응답스펙트럼 비(Ratio of response spectrum, RRS)라 하며, RRS를 사용하여 단주기 지반증폭계수(Fa)와 장주기 지반증폭계수(Fv)는 식 (10)과 같이 산정된다(Borcherdt, 1994; Dobry et al., 1999).
여기서 RSsoil 및 RSrock은 각각 지표면 및 기반암의 주기 T에서의 가속도 응답스펙트럼이며, T1과 T2는 지반증폭계수 산정을 위한 주기 값이다. 본 연구에서는 Manandhar et al.(2017)과 Kim et al.(2018)이 국내 부지에 대해 제안한 연구결과에 근거하여, Fa의 경우 T1 = 0.1sec와 T2 = 0.5sec를, Fv는 T1 = 0.4sec와 T2 = 1.5sec를 적용하여 산정하였다.
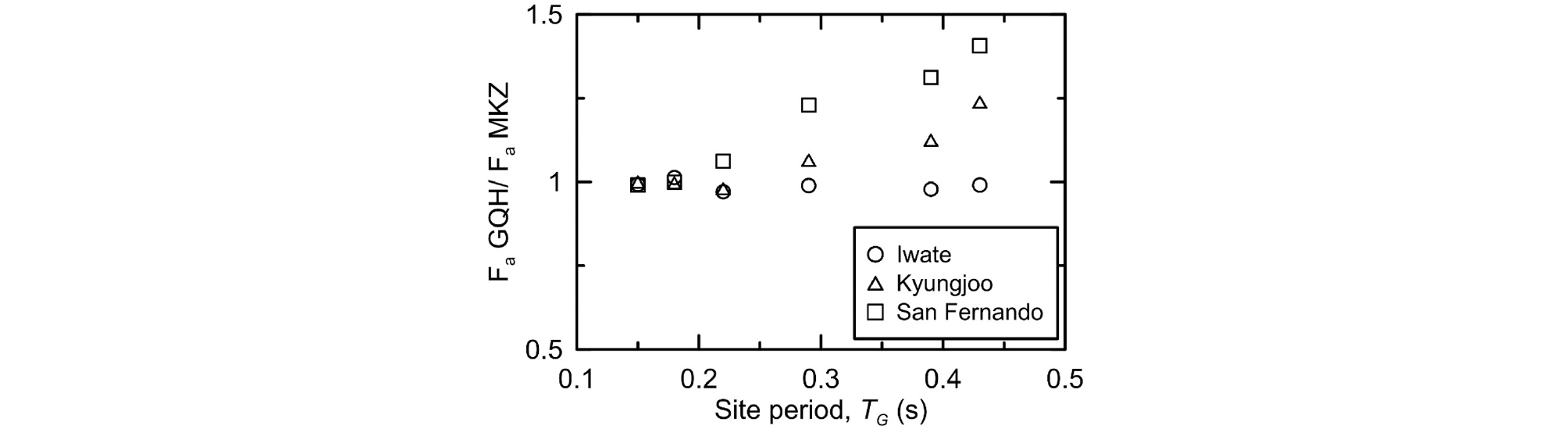
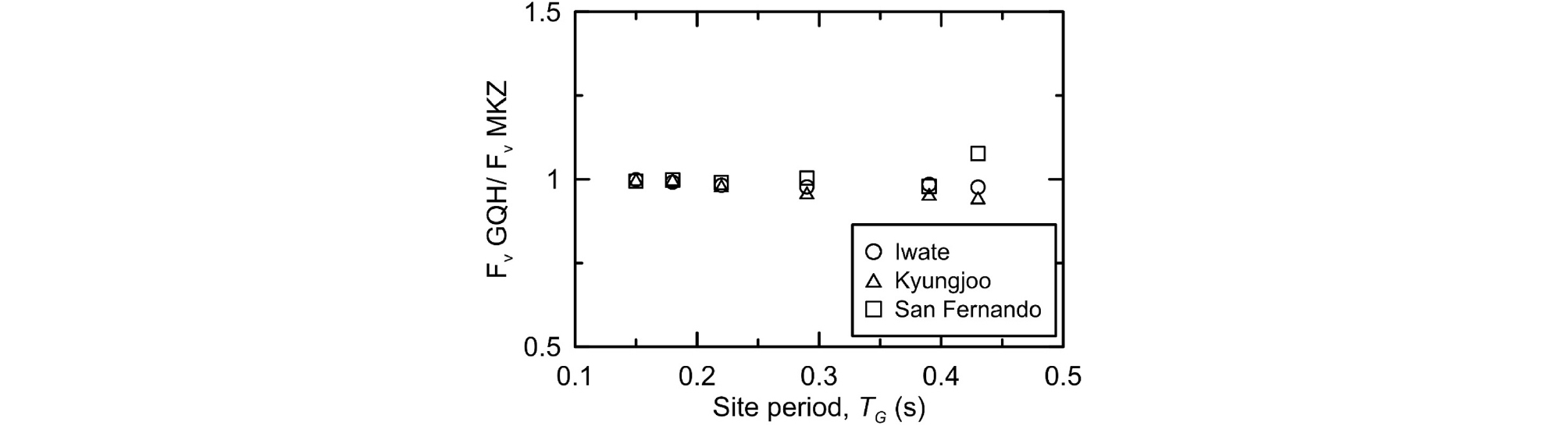
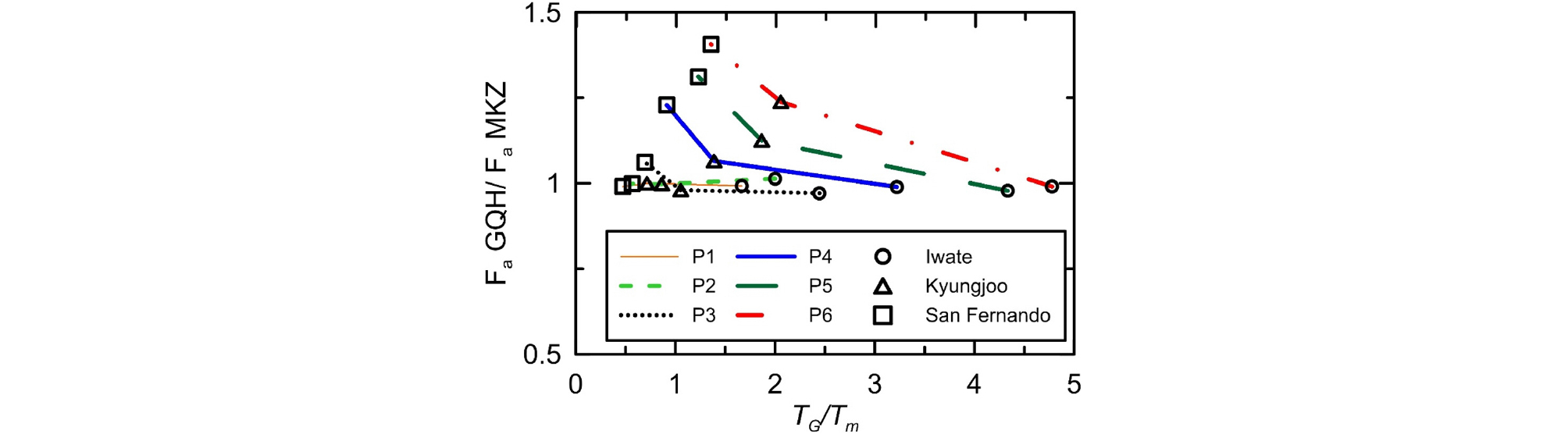
Fig. 9에는 두 모델간의 Fa 비와 TG 간의 관계가 도시되어 있다. 연약지반일수록 Fa 비가 증가함을 확인할 수 있다. TG가 0.43sec인 가장 연약한 지반에서 Fa 비는 1.41이었다. 본 연구에서 사용된 부지의 TG가 모두 0.5sec 미만이며, 이는 Fa 산정 주기 구간인 0.1~0.5sec에 속하므로 두 모델 간의 차이는 더욱 두드러지게 나타났다. 두 모델의 Fv 비와 TG 간의 관계는 Fig. 10에 도시하였다. 모든 부지에서 두 모델의 Fv는 큰 차이를 보이지 않는데, 이는 Fv 산정에 사용된 주기 구간보다 부지 고유주기가 짧기 때문인 것으로 판단된다. 입력지진파에 따른 변화를 분석하면, Tm이 클수록 Fa 비의 변화가 크게 발생하지만 Fv 비는 Tm의 영향이 거의 나타나지 않았다.
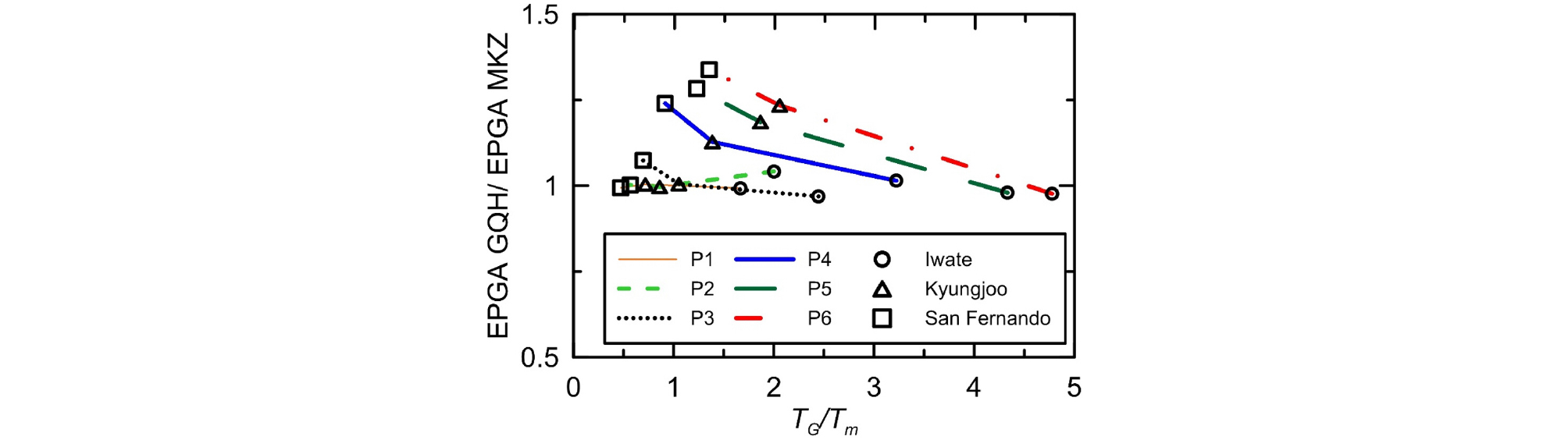
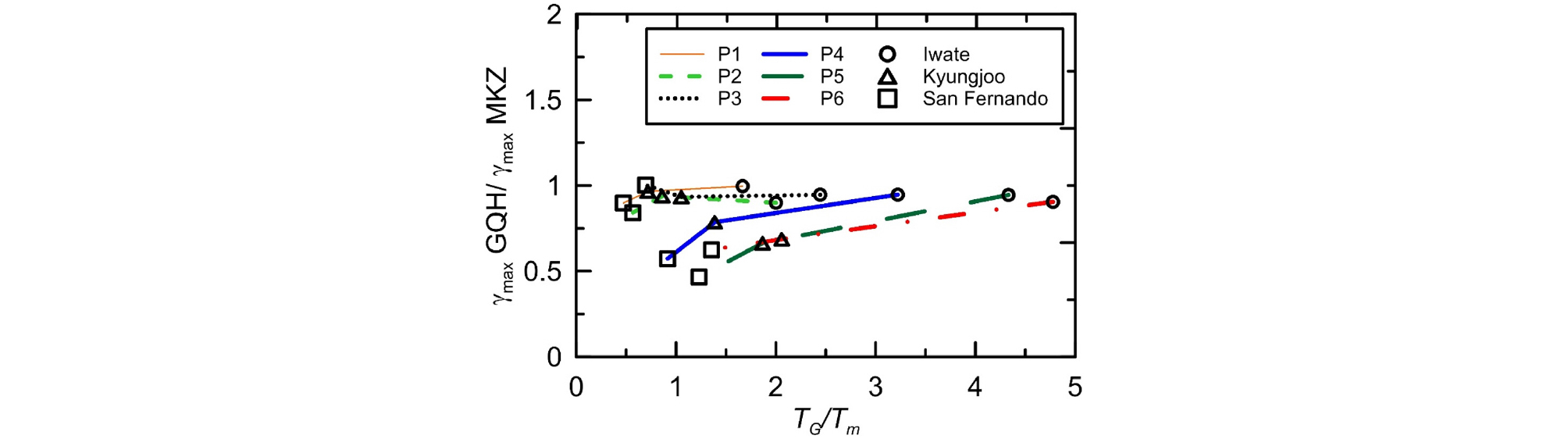
부지의 특성과 함께 입력지진파의 변화에 따른 영향을 분석하기 위해 TG와 Tm의 비(TG/Tm)와 EPGA, 최대전단변형률 간의 관계를 Fig. 11과 Fig. 12에 각각 도시하였다. TG/Tm이 증가할수록 EPGA 비는 감소하는데, 이는 입력지진파의 Tm이 작아질수록 GQ/H 모델과 MKZ 모델로부터 계산된 결과 값의 차이가 커진다는 것을 의미한다. 최대전단변형률 비는 대부분의 부지에서 TG/Tm의 증가에 따라 함께 증가하는 경향을 나타낸다. 위에서 살펴본 바와 같이 전단강도 보정의 영향은 Tm과는 무관하게 TG가 0.2sec 미만인 부지에 대해서는 무시할 수 있는 것으로 판단된다. 입력지진파의 영향은 TG/Tm와 Fa 비가 이루는 경사에 영향을 주며 Tm이 클수록 경사가 급하며 변화가 크게 발생하는 것으로 나타났다. Iwate 지진파의 경우 Fa 비가 상대적으로 작은 반면, Tm이 가장 작아 TG/Tm이 커져 기울기가 작아진다.
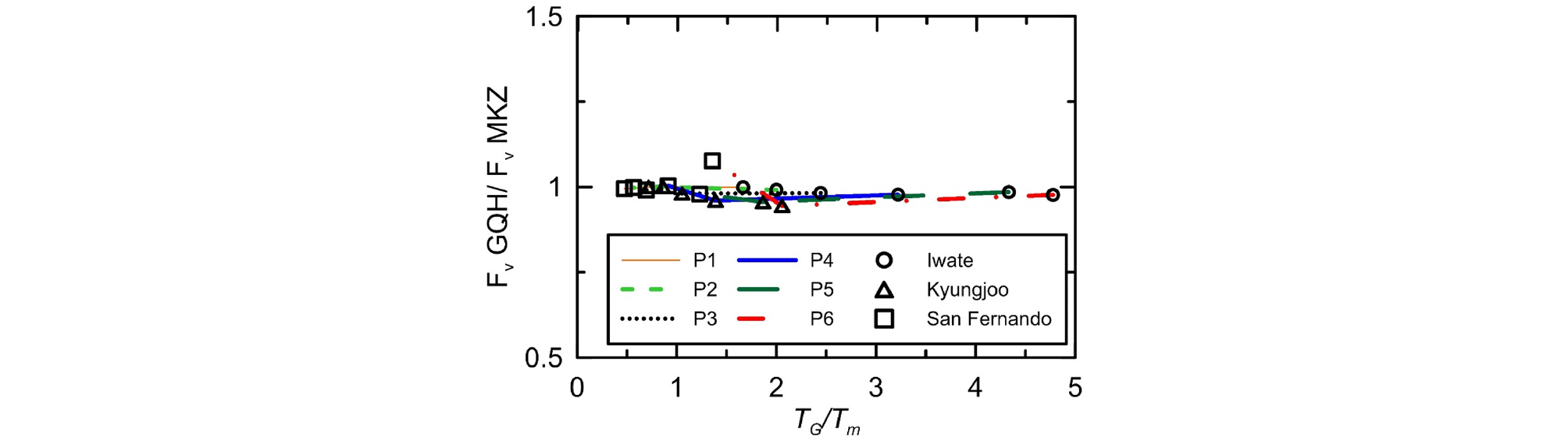
Fig. 13은 전체 부지에 대해 두 모델에서 산정된 Fa 비와 TG/Tm 간의 관계를 보여준다. TG/Tm가 1에 가까워지면 Fa 비가 증가한다. 이러한 경향은 유의미한 변화가 발생하지 않는 P1, P2 부지를 제외한 모든 부지에서 일관적으로 나타났다. 또한, 두 모델에서 산정된 Fa는 Tm이 매우 짧은 입력지진파를 받는 연약한 부지에서는 거의 일치함을 확인할 수 있다. Fig. 14에는 Fv의 비와 TG/Tm 간의 관계를 도시하였다. 앞서 언급한 바와 같이 사용된 부지의 TG가 0.43sec이하이기 때문에, Fv 산정 주기 구간(0.4~1.5sec)에 거의 속하지 않으므로 TG/Tm의 변화에 따른 Fv 비의 변화는 거의 나타나지 않는다.
5. 결 론
본 연구에서는 전단강도 보정이 부지응답해석에 미치는 영향을 평가하였고, 부지 및 입력지진파 특성과의 상관관계를 분석하였다. 이를 위해 국내 6개 부지에 대한 1차원 비선형 부지응답해석을 수행하였다. 해석에는 전단강도 보정 기능을 보유한 MKZ 모델과 GQ/H 모델을 사용하였다. 두 모델에 의한 EPGA 및 최대전단변형률의 변화를 분석한 결과, TG가 증가함에 따라 전단강도 보정이 더욱 중요해진다는 것을 확인하였다. 특히 부지 내에서 Vs가 심도에 따라 감소하는 구간이 존재할 경우 MKZ 모델은 전단강도를 매우 과소산정하기 때문에 적절한 보정이 더욱 필요하다. TG가 0.2sec 미만인 경우, Tm과는 무관하게 전단강도 보정의 영향이 나타나지 않았다. 또한, Tm도 해석 결과에 영향을 주는 것으로 나타났다. Tm이 감소함에 따라 두 모델에 의한 EPGA와 최대전단변형률의 해석 결과가 거의 일치함을 확인하였다. 두 모델에 의한 지반증폭계수 분석을 통해서도 유사한 결론을 도출할 수 있다. 본 연구에서 사용한 얕은 기반암 심도인 부지의 특성으로 인해 Fa의 경우 두 모델 간의 유의한 차이가 나타나지만 Fv는 그 차이가 거의 나타나지 않았다.