1. 서 론
2. 예측 모델
2.1 합성곱 신경망 알고리즘
2.2 입력 이미지
2.3 학습 방법
2.4 학습에 사용된 하드웨어 및 OS
3. 예측 결과
3.1 훈련 정확도
3.2 클래스 활성화 맵
4. 결 론
1. 서 론
최근 건설현장은 지반특성이 복잡하고 위험성이 높은 지역에서의 공사가 급증하고 있다. 특히 터널공사는 지상구조물의 하부통과, 연약대, 파쇄대 통과 등 난공사 구간이 증가하고 있는데, 이러한 구간에서의 터널 붕락사고는 인명 및 재산 피해가 막대하기 때문에 시공 중 막장 암판정을 통해 지보패턴을 적절하게 결정할 필요가 있다. 지보패턴을 결정하기 위하여 암반상태를 평가하는 암반 분류법에는 RMR 분류법(Rock Mass Rating System)과 Q 분류법(Q-System)이 있다.
RMR 분류법(Bieniawski, 1989)은 6가지 요소를 중심으로 세부적으로 평가하여 각 점수를 합산한 총 점수로 암반상태를 평가하는 방법이다. 총점은 0~100점 사이이며, 점수가 높을수록 공학적으로 양호한 암반으로 평가할 수 있다. RMR 분류법에서 6가지 요소는 다음과 같다.
(1) 암석의 일축압축강도
(2) RQD (Rock Quality Designation)
(3) 불연속면의 간격
(4) 불연속면의 상태
(5) 지하수의 상태
(6) 불연속면의 방향성의 영향을 고려하기 위한 보정
RMR 분류법에서는 RMR값에 따라 암반을 Table 1과 같이 1등급에서 5등급까지 구분한다.
Table 1. Rock Quality Classification using RMR rating
| RMR rating | 81~100 | 61~80 | 41~60 | 21~40 | ≤20 |
| Classification | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ |
| Rock quality | Very good | Good | Fair | Poor | Very poor |
Q 분류법은 Barton et al.(1974)에 의해 제시된 암반 분류법으로서 절리의 방향성보다 절리면 간격, 절리면 상태를 중요하게 고려한 방법으로 아래 6가지 분류 요소를 근간으로 한다.
(1) RQD
(2) 절리군 수
(3) 절리면 거칠기
(4) 절리면 풍화도
(5) 절리내 지하수 감소계수
(6) 응력저감계수
여기서 Q값은 0.001~1,000까지 분포할 수 있으며, Q값이 클수록 공학적으로 양호한 지반이다.
이상의 RMR 분류법 및 Q 분류법은 터널을 설계하기 위한 기본 데이터이다. 설계 시의 지반조사로는 암반의 모든 특성을 파악하기 어렵기 때문에, 시공 중 위의 분류법으로 암반 특성을 파악하고 보강하면서 터널 굴진을 해야 한다. 그러나 터널 막장면에 노출된 절리 방향과 길이 등을 모두 관찰하고 이를 지질도로 정리하기 위해서는 숙련된 기술과 많은 시간이 필요하다. 따라서 터널 페이스매핑(Face Mapping)을 통해서 취득하는 정보의 질이 떨어지고 정보의 양이 부족하게 된다. 이와 같은 문제점을 극복하고 더 많은 정보를 체계적으로 얻기 위하여 조사선법(Scanline Method)과 조사창법(Window Method) 등이 고안되었다(Priest, 1993). 두 방법 모두 암반의 절리 특성을 정확하게 조사할 수 있지만 현장에서 실제 이용하기에는 여러 가지 불편한 점이 있다. 특히 조사시간이 길고 얻는 정보가 부족한 문제점이 있다.
터널 페이스매핑 개선 방법으로 디지털 사진(Kim, 2011)이나 LIDAR(Light Detection and Ranging) 스캔(Kim and John, 2009) 등의 디지털 기술을 이용하여 암반의 특성을 분석하려는 연구가 이루어지고 있다. 디지털 사진 방법(Kim, 2011)은 사진기로 촬영한 터널 막장면 사진으로부터 소프트웨어를 이용하여 점군을 생성하고 터널 막장면에 분포한 여러 절리의 특성을 추출한다. 이 방법은 디지털 사진으로부터 3차원 좌표를 만드는 과정이 복잡하다.
LIDAR 스캔 방법(Kim and John, 2009)은 좌표 값이 3차원으로 스캔되므로 좌표 값에 대한 별도의 처리과정이 필요하지 않은 장점이 있다. LIDAR의 스캔결과는 레이저가 투사된 점을 3차원 좌표 값으로 표시한 것으로 투사간격에 따라 수백만 개 이상의 점에서 좌표 값이 측정된다. 이로부터 암반 내 절리의 방향, 길이, 간격 등을 구할 수 있다. 다만 장비가격이 디지털 사진기보다 훨씬 비싼 단점이 있다.
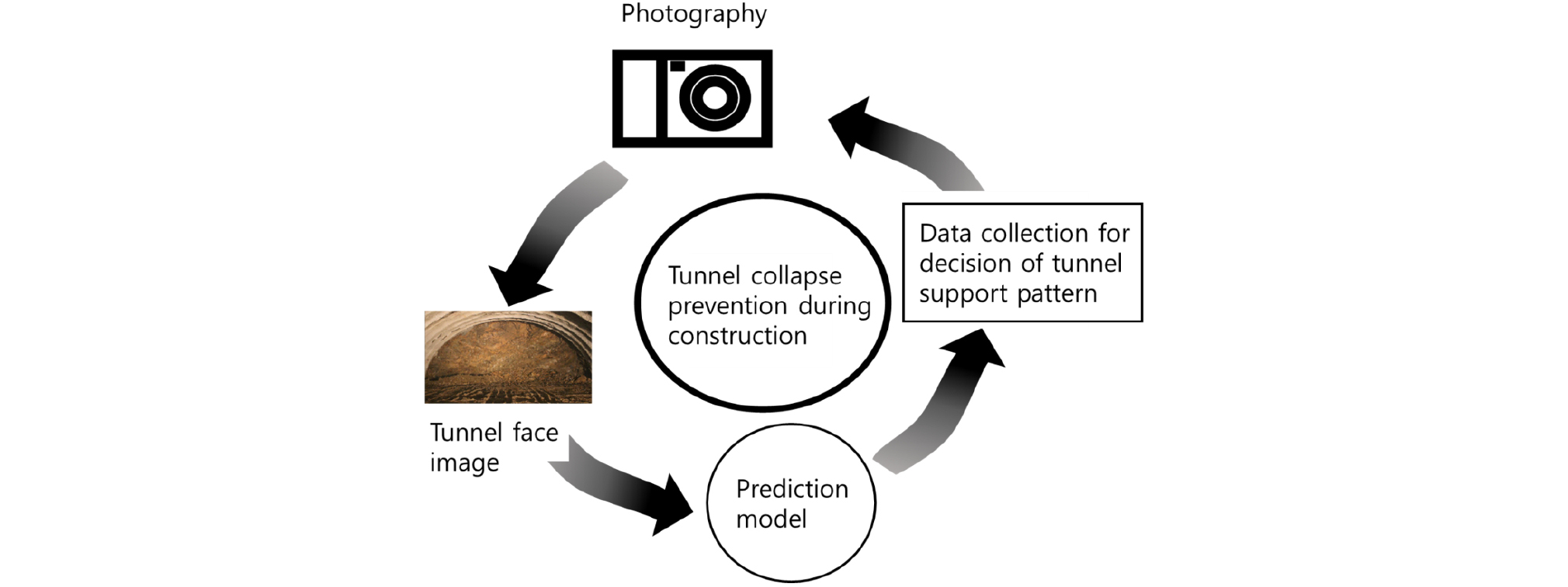
최근 딥러닝 기술은 프로그래밍으로는 해결하기 어려웠던 시각과 청각 같은 지각의 문제에서 괄목할 만한 성과를 내고 있다(Chollet, 2018). 특히 이미지 판독 기술은 의료분야에서 암진단에 높은 정확도를 나타내고 있고, 완전한 자율주행 자동차의 개발도 곧 이루어질 것으로 기대되고 있다. 그러나 지반공학 분야에서 딥러닝 기술이 적용된 사례는 미미하다. 본 연구에서는 딥러닝 기법 중 이미지 분석에 성능이 뛰어난 합성곱 신경망(Convolutional Neural Network, CNN) 알고리즘을 활용하여 터널 막장면 이미지로부터 암반의 특성을 신속하게 분석하는 기술을 개발하는데 목적이 있다. 이 기술은 전문가에 따라 발생하는 터널의 암반특성 평가의 차이를 줄이고, 터널 시공 중 붕락사고를 사전에 예방하는데 기여할 수 있을 것으로 기대된다(Fig. 1).
2. 예측 모델
2.1 합성곱 신경망 알고리즘
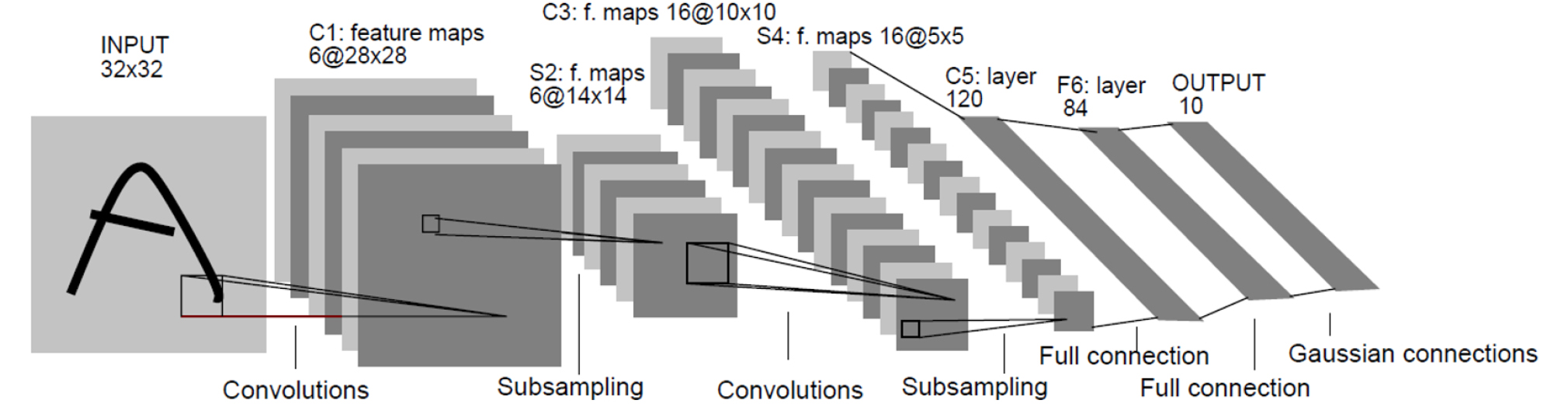
Hubel and Wiesel(1959)은 고양이 머리에 전극을 부착하여 서로 다른 시각적 자극을 주었을 때 어떻게 반응하는지 관찰하였다. 고양이에게 어떤 이미지를 보여주었더니 그림을 읽어 들이는 뉴런들이 동시에 동작하는 것이 아니라, 특정 그림의 특정 부분에 대해서만 동작하는 것을 알게 되었다. 어떤 뉴런은 수직선의 이미지에만 반응하고, 다른 뉴런은 수평선이 있을 때만, 또 다른 뉴런들은 특정 각도의 선에 반응한다는 것이다. 또한 시각 피질은 여러 층으로 구조화 되어있고, 각 층은 선, 윤곽선, 형태, 전체 객체 등 이전 층에서 감지된 특징들을 그 위에 쌓는다는 것을 관찰하였다. 이러한 아이디어가 바로 합성곱 신경망으로 점차 진화되어 왔으며, Lecun et al.(1998)에서는 손글씨 숫자를 인식하는데 사용한 LeNet-5가 소개되면서 합성곱 신경망이 등장하게 되었다.
합성곱 신경망은 Fig. 2(Lecun et al., 1998)와 같이 하나 또는 여러 개의 합성곱 층과 그 위에 올려진 일반적인 인공 신경망 층들로 이루어져 있으며, 가중치(Weight)와 통합 계층(Pooling Layer)들을 추가로 활용한다. 이러한 구조 덕분에 합성곱 신경망은 2차원 구조의 입력 데이터를 충분히 활용할 수 있다. 다른 딥러닝 구조들과 비교해서, 합성곱 신경망은 영상, 음성 분야 모두에서 좋은 성능을 보여준다. 또한 다른 인공 신경망 기법들보다 쉽게 훈련되는 편이고 적은 수의 파라미터를 사용한다는 이점이 있다(Chollet, 2018).
합성곱 신경망의 핵심 특징은 학습된 패턴의 평행 이동 불변성이다. 이 특징은 이미지의 어떤 위치에서 특정 패턴을 학습하였다면 다른 위치에서도 이 패턴을 인식할 수 있게 한다. 근본적으로 우리가 사물의 특징을 파악하는 것과 같은 방법이다. 따라서 적은 수의 훈련 샘플을 사용해서 일반화 능력을 가진 샘플을 학습할 수 있다. 합성곱 신경망의 또 다른 특징은 패턴의 공간적 계층 구조를 학습할 수 있는 것이다. 첫 번째 합성곱 층이 에지 같은 작은 지역 패턴을 학습한다. 두 번째 합성곱 층은 첫 번째 층의 특성으로 구성된 더 큰 패턴을 학습하는 방식이다. 이런 특징으로 매우 복잡하고 추상적인 시각적 개념을 효과적으로 학습할 수 있다(Chollet, 2018).
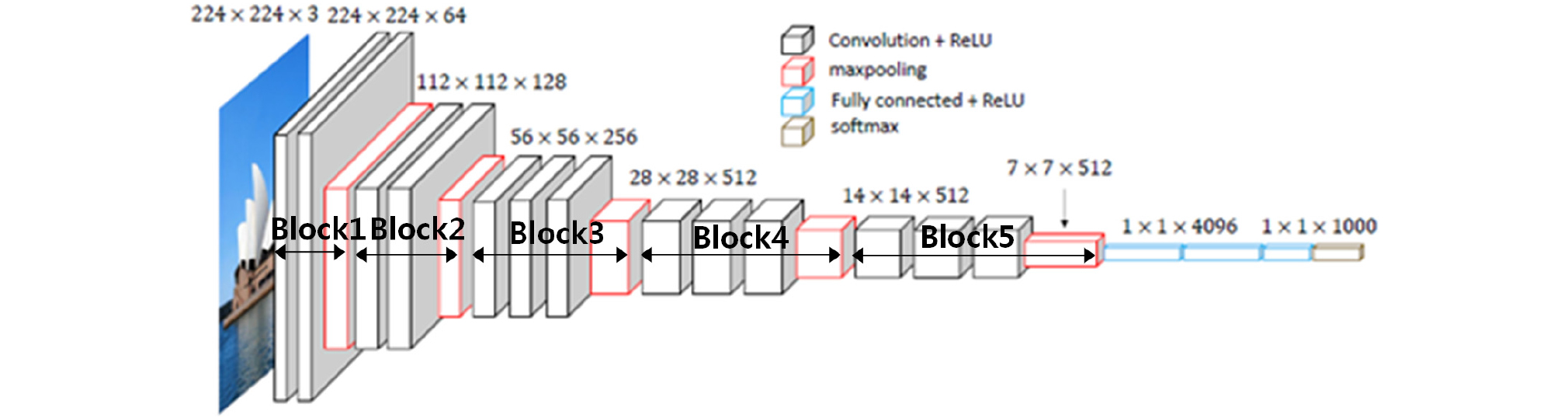
본 논문에서는 사전 훈련된 VGG16 모델을 활용하였다(Simonyan and Zisserman, 2015). 이 모델은 옥스포드 대학의 연구팀에 의해 개발되었고, 합성곱 신경망의 간단한 구조로 이루어져 있음에도 높은 성능을 나타낸다. VGG16 모델은 Fig. 3에 나타낸 것과 같이 13개의 합성곱 층과 3개의 완전 연결(Fully Connected) 계층의 구조이며, 합성곱 층을 거쳐서 추출된 특징들은 서브 샘플링의 과정을 거친다. 서브 샘플링이란 고해상도 사진을 보고 물체를 판별할 수 있지만 작은 사진을 가지고도 그 사진의 내용이 어떤 사진인지 판단할 수 있는 원리로, 합성곱 층을 거쳐서 추출된 특징을 인위적으로 사이즈를 줄이는 작업이다. 서브 샘플링은 전체 데이터의 사이즈를 줄여 연산을 적게 할 수 있고 과적합(Overfitting)을 방지할 수 있는 장점이 있다. VGG16 모델에서는 서브 샘플링 방법으로 맥스플링(Max Pooling)이 적용되었다(Gardezi et al., 2017). 맥스플링은 정해진 픽셀마다 최대값을 뽑아내는 것으로, 데이터의 크기를 줄일 수 있고 과적합을 방지할 수 있다. 합성곱 층을 통해서 특성맵이 추출되는데 이 특성맵에 활성화 함수(Activation Function)로 ReLU 함수가 사용되었다(Nair and Hinton, 2010). 활성화 함수란 입력 신호의 총합을 출력 신호로 변환하는 함수를 말하며, 사용된 ReLU 함수는 입력이 0 이상이면 입력을 그대로 출력하고, 0 이하이면 0을 출력하는 함수 이다. ReLU 함수를 식 (1)에 나타낸다(Jarrett et al., 2009).
| $$ReLU(x)=max(0,x)$$ | (1) |
완전연결 계층은 입력신호를 직렬화하여 이미지에 대한 분류(Classification) 결과를 얻는다. 완전연결 계층의 마지막 활성화 함수로는 Softmax가 사용되었다. Softmax(Bishop, 2006)는 입력된 값을 0~1 사이의 출력값으로 모두 정규화하며 출력 값들의 총합은 항상 1이 되는 특성을 가진 함수이다. Softmax 함수를 식 (2)에 나타내었다.
| $$y_k=\frac{e^{a_k}}{\sum_{i=1}^ne^{a_i}}$$ | (2) |
여기서 n은 출력 층의 뉴런 수, ak는 k번째 입력신호, 분모는 모든 입력신호의 지수함수 합이며, yk는 k번째 출력을 뜻한다.
Keras에서는 1,400만개의 레이블된 다양한 종류의 이미지와 1,000개의 클래스로 이루어진 ImageNet 데이터셋에서 사전에 학습되어 있는 VGG16, ResNet50 등의 파라미터 가중치를 제공한다(Chollet, 2018). 본 연구에서는 예측 성능이 뛰어나고 상대적으로 간결한 모델인 VGG16을 활용하였다. 그러나 ImageNet 원본 데이터셋은 대부분 동물이나 생활 용품으로 이루어진 이미지로 터널의 막장면 데이터셋과는 많은 차이가 있다. 이를 해결하기 위하여 지보패턴 예측에는 VGG16 모델의 사전 학습된 합성곱 층의 가중치(Weight)만을 활용하였으며, VGG16의 사전 학습된 합성곱 층에 학습되지 않은 새로운 4개의 완전연결 계층을 연결하여 학습시켰다. 완전연결 계층의 마지막 활성화 함수로는 Softmax를 사용하였고, 5개의 타입으로 분류할 수 있게 하였다.
2.2 입력 이미지
학습을 위한 입력 이미지 데이터셋을 Table 2에 나타낸다. 각 이미지는 5가지 타입으로 레이블 되었으며, 이는 Table 1의 RMR 총점을 이용한 암반분류 등급과 일치한다. 예측모델 학습에는 총 1,469개의 이미지가 사용되었으며, 과적합을 방지하기 위한 검증 이미지로 338개의 이미지를 별도로 마련하였다. 또한 모델 학습 후 학습에 사용하지 않은 473개의 이미지 데이터로 예측 정확도를 평가하였다.
Table 2. Data sets of input images
| Type | Training set | Validation set | Test set |
| Type 1 | 17 | 6 | 8 |
| Type 2 | 525 | 124 | 157 |
| Type 3 | 307 | 61 | 101 |
| Type 4 | 435 | 96 | 135 |
| Type 5 | 185 | 51 | 72 |
| Total | 1,469 | 338 | 473 |
입력 이미지의 적합한 크기를 결정하기 위하여 입력 이미지 크기를 변화시키면서 VGG16 모델의 사전 학습된 합성곱 층의 가중치는 동결하여 재학습이 이루어지지 않도록 하고 추가된 새로운 4개의 완전연결 계층만을 학습시켰다. 그 결과를 Table 3에 나타내었다. Case No.1과 Case No.2를 비교하면 입력 이미지 크기가 줄어들지만 예측 정확도는 거의 일치 하고, 훈련시간은 매우 적어지는 경향을 보인다. 그러나 입력 이미지 크기가 300×180 픽셀보다 더 작아지면 예측 정확도는 감소하고 오히려 훈련시간이 증가하는 경향을 나타냈다. 따라서, 입력 이미지의 크기가 300×180 픽셀 이하의 이미지에서는 정보의 손실이 발생한다고 판단되어, 본 연구에서는 모든 입력 이미지의 크기를 300×180 픽셀로 고정하였다. 전형적인 입력 이미지의 샘플을 Fig. 4에 나타내었다.
Table 3. Calculation results to determine the size of input images
| Case No. |
Image size (width×height, Pixel) | Loss rate | Accuracy |
Training time (Minute) |
| 1 | 900×540 | 0.753 | 0.761 | 307.6 |
| 2 | 300×180 | 0.670 | 0.773 | 24.6 |
| 3 | 100×60 | 0.644 | 0.748 | 30.0 |
| 4 | 80×48 | 0.699 | 0.701 | 31.8 |
2.3 학습 방법
모델을 재사용하기 위하여 미세조정(fine-tuning) 방법을 이용하였다(Chollet, 2018). 주어진 문제에 맞게 재사용 모델의 가중치를 조정하기 때문에 미세조정이라 부른다. 그러나 새로운 4개의 완전연결 계층이 미리 훈련되지 않은 상태에서 모델 전체를 학습시키면 사전 학습된 표현들이 망가지게 되므로 다음과 같은 단계로 모델의 미세조정을 진행하였다.
(1) VGG16 모델의 사전 학습된 합성곱 층에 새로운 4개의 완전연결 계층을 추가한다.
(2) VGG16 모델의 사전 학습된 합성곱 층을 동결(freezing)하여 학습이 이루어지지 않도록 한다.
(3) 막장면 이미지로 새로 추가한 4개의 완전연결 계층을 훈련한다.
(4) VGG16 모델의 사전 학습된 합성곱 층의 일부 층을 동결 해제한다.
(5) 동결을 해제한 층과 새로 추가한 4개의 완전연결 계층을 미세조정 방법으로 훈련한다.
이와 같은 미세조정 방법은 새로운 문제가 원래 학습된 이미지와 완전히 다른 종류의 것이더라도 매우 효과적으로 작동하며, 작은 데이터셋을 가진 문제에도 효율적으로 작동하는 것으로 알려져 있다(Chollet, 2018).
2.4 학습에 사용된 하드웨어 및 OS
합성곱은 행렬 계산의 반복작업으로 이루어져 있고, 이와 같은 행렬 계산에는 그래픽카드(GPU)가 고사양일수록 빠른 처리능력을 나타낸다. 이번 연구에 사용된 컴퓨터 하드웨어를 Table 4에 나타내었다. 연산에 사용된 그래픽카드는 NVIDIA GeForce GTX 1050Ti이며 그래픽카드 메모리는 4GB이다.
Table 4. Computer hardware and operating system
| Hardware | Specification |
| GPU | NVIDIA GeForce GTX 1050Ti, Memory: 4 GB |
| CPU | Intel Core i7-6700k |
| RAM | 32 GB |
| Operating system | 64 bit Windows 7 |
3. 예측 결과
3.1 훈련 정확도
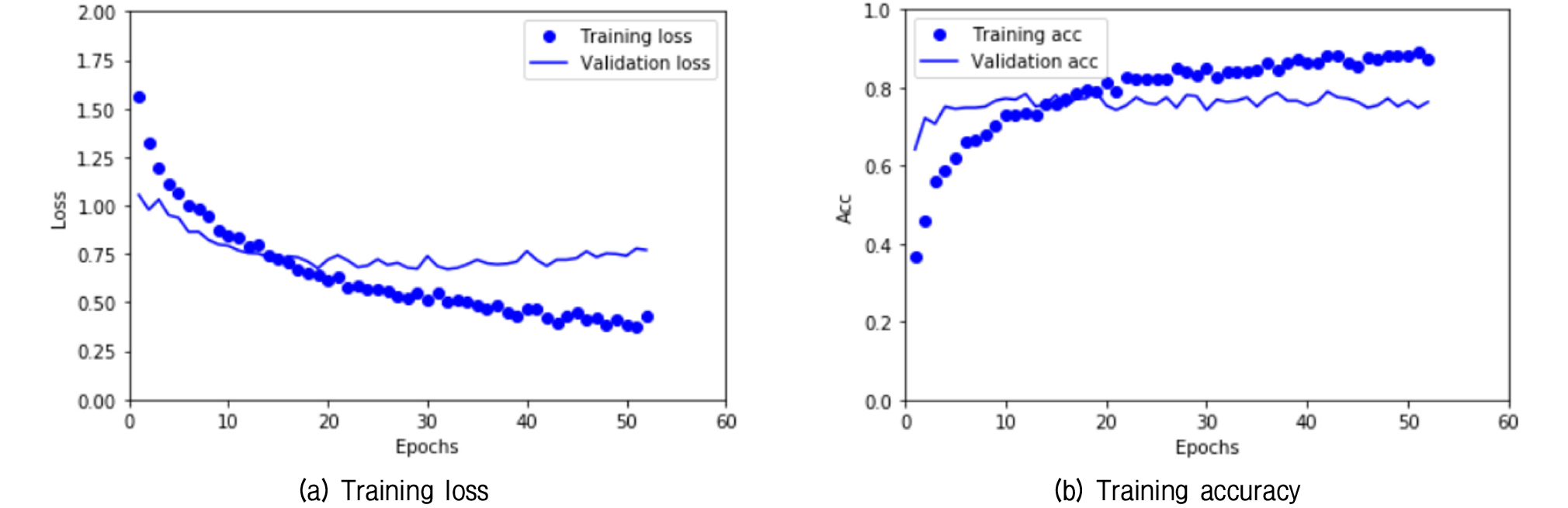
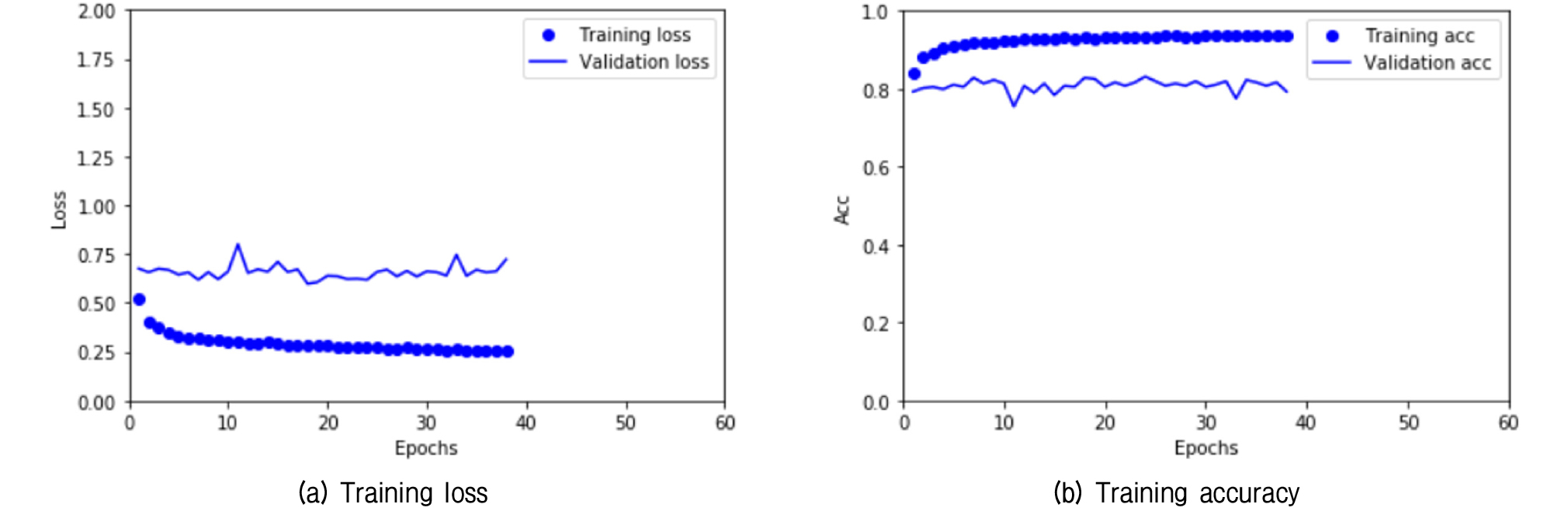
먼저 Table 2의 입력 이미지 데이터셋으로 VGG16 모델의 사전 학습된 합성곱 층을 동결한 후 새로 추가한 4개의 완전연결 계층을 훈련한 훈련 손실과 정확도 곡선을 Fig. 5에 나타내었다. 여기에서 손실이란 오차를 의미하며 정답에 가까워질수록 손실 값은 작아진다. 정확도는 분류하고자 하는 데이터셋 중에서 정답으로 분류한 수의 확률을 나타낸다. 훈련 손실은 지속적으로 감소하나 검증 손실은 훈련 초기 단계에 최저치에 도달하고 있다. 훈련 정확도는 훈련 단계가 증가함에 따라서 지속적으로 증가하나 검증 정확도는 빠른 시점에서 80%정도에 머무른다. 훈련 이미지가 부족하여 빠르게 과적합이 일어나고 있다고 판단된다.
앞서 제시한 미세조정 방법으로 완전연결 계층의 학습된 가중치를 사용하고 Fig. 3에서 나타낸 합성곱 층의 Block 1, 2는 동결하여 가중치가 학습되지 않도록 동결하고, Block 3, 4, 5는 동결 해제하여 미세조정으로 재학습하는 경우의 훈련 손실과 정확도 곡선을 Fig. 6에 나타내었다. 여기에서 Block 1과 Block 2는 2개의 합성곱 층과 1개의 맥스플링으로 이루어졌고, Block 3, 4, 5는 3개의 합성곱 층과 1개의 맥스플링으로 이루어져 있다. 학습 시에는 미세조정 하는 3개의 Block 층에서 학습된 표현을 조금씩 수정하기 위하여 학습률(Learning Rage, LR)을 낮추었다. 학습률이란 한번 갱신하는 가중치의 값을 말하는데 학습률이 너무 작게하면 학습되는 속도가 너무 작아서 많은 학습시간이 걸리고, 너무 크면 최적의 값을 계속 지나치게 된다. 본 연구에서는 학습률을 미세조정에서 일반적으로 사용하는 LR=10-5로 하였으며 원활하게 학습되는 것을 확인하였다. 이는 변경량이 너무 크면 사전 학습된 가중치에 나쁜 영향을 끼칠 수 있기 때문이다. Fig. 6에서 훈련 손실과 훈련 정확도는 약간 향상되고 있지만, 검증손실과 검증 정확도는 거의 변화가 없는 것처럼 보인다. 이러한 현상은 미세조정하는 Block을 변화시켜도 비슷한 양상을 보였다. 다만 미세조정하는 Block이 많아지면 훈련해야 할 파라미터가 많아지므로 훈련 횟수(Epoch)가 증가하는 경향을 보였다.
미세조정 Block 수에 따른 손실율과 정확도를 Table 5에 나타낸다. 여기에서 손실율과 정확도는 훈련 데이터셋으로 훈련한 후에 시험 데이터셋으로 손실율과 정확도를 확인한 결과이다. 미세조정 Block이 많아지면 손실율이 작아지고 정확도는 증가하는 경향을 보인다. 그러나 미세조정 Block이 3, 4, 5이상일 경우에는 손실율이나 정확도가 향상되지 않는다. 이는 미세조정하여야 할 합성곱 Block 수가 많아지면 많아질수록 훈련해야 할 파라미터 수가 증가하고 이로 인해 과적합이 일어나기 때문인 것으로 예상된다. 따라서 훈련시간 단축 및 정확도 향상을 휘해서는 Block 3, 4, 5까지만 미세조정하는 것이 적합할 것으로 판단된다. Table 5에 나타낸 바와 같이 입력 데이터에 대하여 가장 좋은 정확도는 0.839를 기록하였다. 같은 모델로 미세조정 방법을 사용하지 않고 랜덤 가중치값을 초기치로 훈련하였을 때 결과값은 손실율이 0.759이고, 정확도는 0.767이였다. 따라서 미세조정 방법은 합성곱 신경망 기법에서 효과적으로 정확도를 향상시킬 수 있음을 알 수 있다.
Table 5. Loss rate and accuracy by the number of fine-tuning blocks
| Fine-tuning block | Loss rate | Accuracy |
| 0 (Fixed in all blocks) | 0.674 | 0.774 |
| 5 | 0.639 | 0.803 |
| 4,5 | 0.605 | 0.814 |
| 3,4,5 | 0.554 | 0.839 |
| 2,3,4,5 | 0.555 | 0.837 |
| 1,2,3,4,5 | 0.589 | 0.837 |
3.2 클래스 활성화 맵
이미지의 어느 부분이 합성곱의 최종 분류 결정에 기여하는지 이해하는 데 유용한 방법으로 클래스 활성화 맵(Class Activation Map) 시각화가 있다(Chollet, 2018). 이 기법은 입력 이미지에 대한 클래스 활성화의 히트맵(Heatmap)을 만든다. 히트맵은 클래스에 대해 입력이미지의 각 위치가 얼마나 중요한지 알 수 있게 해 준다. 이 기법은 클래스에 대한 각 채널의 중요도로 가중치를 부여하여 입력 이미지가 클래스를 활성화하는 정도에 대한 공간적인 맵을 만드는 것이다.
4 타입으로 분류되는 입력 이미지에 대한 클래스 활성화 히트맵을 Fig. 7에 나타내었다. 원본 이미지를 확인하면 하부는 연암질 암반이 출현하나, 부분적으로 파쇄/풍화대가 발달하고 있다. 천단부 상태는 풍화암에서 연암으로 변화하는 경계부에 해당하여 4 타입으로 구분할 수 있다. 클래스 활성화 히트맵에서도 파쇄대가 발달하는 곳이 활성화되어, 예측모델은 90% 확률로 4 타입으로 예측되었다.
5 타입으로 분류되는 이미지에 대한 클래스 활성화 히트맵을 Fig. 8에 나타내었다. 막장면은 전반적으로 풍화 정도가 심하고, 대부분의 불연속면에 점토질이 협재되어 있을 뿐 아니라, 중앙부 불연속면은 매우 미끄러운 상태의 단층활면으로 보인다. 암질은 풍화암으로 하부 버럭이 대부분 토사 및 세편화되어 있어 5 타입으로 판정된다. 예측 결과의 히트맵은 불연속면을 따라 요철이 가장 심한 부분을 표시하였으며, 5 타입으로 판정되었다. 지질기술자의 판단기준인 점토질 협재, 단층활면(Slickenside) 등과는 상이한 측면이 있다.
5 타입으로 분류되었지만 4 타입으로 예측된 경우의 클래스 활성화 히트맵의 예를 Fig. 9에 나타내었다. 막장면은 풍화암과 연암의 경계 정도의 암질로 평가된다. 터널과 직교하며 수직으로 발달하는 불연속면으로 인하여 막장면에는 불연속면이 잘 인지되지 않으나, 벽면은 요철이 심하게 나타난다. 모델의 클래스 활성화 히트맵으로 보면 수직 절리보다는 벽면의 요철부와 중앙부의 뚜렷한 불연속면이 활성화되었고 4 타입으로 판정되었다. 모델은 상대적으로 절리에서 활성화되는 것으로 보인다.
4. 결 론
본 연구에서는 딥러닝 기법을 활용하여 터널막장 이미지로부터 암반등급을 5개로 분류하는 기술을 개발하였다. 예측 결과에 대한 정확도를 평가한 결과 80% 이상의 높은 정확도를 보였으며, 향후 실제 현장에 적용 가능성이 있음을 확인하였다. 본 연구의 결과를 정리하면 다음과 같다.
(1) 사전 훈련된 VGG16 모델을 활용하여 미세조정 방법으로 터널막장 이미지를 학습시킨 결과, 훈련 데이터가 1,469개로 한정적임에도 불구하고 83.9%의 높은 예측 정확도로 암반등급을 분류할 수 있었다.
(2) 클래스 활성화 히트맵 기법으로 모델이 막장면의 절리, 요철 등 불연속면에서 활성화되는 것을 확인하였다.
(3) 입력 이미지의 타입이 다르게 예측된 경우에도 가까운 타입으로 예측되는 경향이 있었다.
(4) 향후 데이터 축적을 통해 전문가에 따른 편차를 줄인 암반등급 분류 방법으로 활용 가능할 것으로 판단된다.