1. 서 론
2. Coupled Eulerian-Lagrangian(CEL) 기법
3. CEL 기법을 활용한 유한요소해석 모델의 극한 파괴 상태 기준 제시
3.1 비배수 상태의 지반 위에 놓인 연속기초(Strip Footing)의 극한 지지력 산정 문제
3.2 CEL 모델링
3.3 해석 결과
3.4 설정된 물리량 기준의 적합성 검증
4. 결 론
1. 서 론
현재 대부분의 지반 구조물 설계는 전통적인 Terzaghi(1943)의 한계평형법(Limit Equilibrium Approach)을 따르고 있다. 현재까지 수많은 한계평형법 이론들이 제안되었지만, 모든 이론에서 공통적으로 필요한 사항은 극한 파괴 상태(Ultimate Failure Condition)에서 나타나는 파괴 전단면(Slip Line)을 찾아야 한다는 점이다. Griffith and Lane(1999)은 유한요소해석을 이용하여 모어 쿨롬 소성 모델의 점착력(c')과 내부마찰각(')을 일정한 비율로 계속 감소시켜서 사면의 최종 안전율과 파괴 전단면을 찾을 수 있는 강도 감소법(Strength Reduction Method)을 제안하였다. 강도 감소법은 비교적 간단하고 객관적인 방법으로 주어진 극한 파괴 상태에 놓인 지반 구조물의 파괴 전단면을 특정할 수 있다는 점에서 다수의 지반 공학 문제에서 폭넓게 사용되고 있다(Zienkiewicz and Tayor, 1989; Griffith and Lane, 1999; Luan et al., 2003; Bui et al., 2011; Chok et al., 2015; El-Garhy and Elsawy, 2017; Chen and Zhang, 2018).
유한요소해석을 이용한 강도 감소법에서 지반의 안전율을 정확하게 구하기 위해서는 극한 파괴 상태(Ultimate Failure Condition)에 대한 명확한 정의가 필요하다. Zienkiewicz and Taylor(1989)와 Griffith and Lane(1999)은 비선형 유한요소해석의 수치 해(Numerical Solution)가 일정 반복 횟수 이내에 수렴하지 않으면 극한 파괴 상태에 도달하였다고 간주하였으며, 이후 대부분의 관련 연구(Luan et al., 2003; Gu et al., 2014; Dai et al., 2017)에서도 유사한 방법으로 극한 파괴 상태 도달 여부를 판단하고 있다.
라그랑주 요소(Lagrangian Elements)를 사용하여 연속체를 표현하는 기존의 유한요소해석 방법은 대변형 발생 시 유한요소 격자망의 뒤틀림이 강성행렬의 악조건(Ill-condition)을 야기하고 이로 인해 해의 비수렴(Non-convergence of Solution) 상황이 발생할 수 있다. 따라서 라그랑주 요소를 사용하는 FEM 해석에서는 Zienkiewicz and Taylor(1989)와 Griffith and Lane(1999)의 방법으로 극한 파괴 시점을 적절하게 감지할 수 있다.
최근 FEM 기법의 빠른 발전과 함께 연속체의 대변형 상태를 해석할 수 있는 다양한 기법이 제안되고 있다. 이 중 과도한 소성 변형이 빈번하게 발생하는 연약지반의 대변형 상태를 적절하게 표현할 수 있는 기법은 Coupled Eulerian-Lagrangian(CEL) 기법이다. CEL 기법은 상대적으로 강성이 작아 대변형이 예상되는 재료에 대해서는 오일러 요소(Eulerian Elements)를 사용하고 그렇지 않은 재료에 대해서는 라그랑주 요소를 사용하여 복합 해석하는 FEM 해석 기법이다. 따라서 CEL 기법을 이용하여 지반은 오일러 요소로 그리고 기초구조물은 라그랑주 요소로 모델링하면 연약지반이 극한 파괴 상태에 도달하여도 오일러 방법의 특성에 의해 앞서 언급한 해의 비수렴 상황은 발생하지 않는다. 따라서 강도감소법을 이용하여 안전율을 찾기 위해 CEL 기법을 사용한다면 해의 비수렴 상황을 가정하였던 Zienkiewicz and Taylor(1989)와 Griffith and Lane(1999)의 방법을 이용하여 극한 파괴 시점을 찾기는 어렵다. 하지만 CEL 기법을 활용한 유한요소해석 모델의 극한 파괴 상태를 평가하는 연구는 미비하여 관련 연구가 필요한 실정이다.
본 연구에서는 CEL 기법을 이용하여 지반 재료의 변형을 모델링할 때 지반의 극한 파괴 상태를 정량적으로 감지할 수 있는 물리량 기준을 제시하고자 한다. 정확한 이론해가 존재하는 연속기초(Strip Footing)의 극한 지지력 산정 문제를 CEL 기법으로 해석하였다. 기초에 작용하는 하중이 극한 파괴 상태 지지력의 이론값에 도달할 때 소성 변형률, 전단응력과 에너지 등 다양한 물리량들이 어떻게 반응하는지 관측하고 분석하였다. 분석 결과로부터 지반의 극한 파괴 상태를 감지할 수 있는 정량적 물리량 기준을 설정하였다. 또한 설정된 기준을 이용하여 서로 다른 해석 조건에 대한 극한 파괴 상태를 적절하게 감지할 수 있는지 조사하였다.
2. Coupled Eulerian-Lagrangian(CEL) 기법
CEL 기법은 물체의 거동을 표현하기 위해 라그랑주 방법의 장점과 오일러 방법의 장점을 접목시킨 수치해석 기법으로 주로 대변형 해석기법에서 사용된다.
라그랑주 방법은 요소의 절점을 재료 안에 구속하여 재료가 변형을 일으키면 요소도 함께 변화한다. 즉 요소 경계와 물질 경계가 일치한다. 따라서 라그랑주 방법으로 정의된 요소들은 각각 오직 한 가지 재료로 이루어진다. 라그랑주 방법은 접촉면의 경계가 명확하기 때문에 표면이나 경계에서의 거동을 추적하기 용이하다. 하지만 대변형 해석과 같이 짧은 시간 안에 급격한 변형을 일으키는 문제에서는 유한요소 격자망의 과도한 일그러짐 문제가 발생할 수 있다. 심각하게 일그러진 유한요소 격자망은 수치해석적으로 강성 행렬의 악조건(Ill-condition)을 야기시키며 해석이 수행되지 않을 수도 있다.
오일러 방법은 재료가 변형을 일으켜도 요소의 절점은 변화하지 않고 공간상의 위치를 고수한다. 오일러 방법으로 정의된 요소들은 서로 다른 두 가지 재료로 구성될 수 있으며, 각 재료의 체적비로 재료의 상태를 표현한다. 오일러 방법의 계산 절차는 다음과 같다. 먼저 라그랑주 방법을 이용하여 주어진 절점 변위에 따라 요소망을 변형시킨다. 이후 주어진 구성 방정식(Constitutive Equation)을 이용하여 서로 연결된 두 요소를 통과하는 재료의 흐름(Material Flow)을 계산한다. 계산이 끝나면 변형된 요소망을 다시 초기 상태로 원위치 시킨 후 계산된 재료의 흐름을 고려하여 각 요소에서 재료가 차지하는 체적비를 갱신한다. 따라서 오일러 방법에서는 유한요소 격자망의 과도한 일그러짐 문제가 발생하지 않으며, 대변형 해석에서 재료의 급격한 변형을 효과적으로 표현할 수 있다.
CEL 기법은 라그랑주 방법과 오일러 방법을 모두 사용하여 요소를 정의한다. 상대적으로 강성이 커서 변형이 적게 일어나는 요소는 라그랑주 방법으로, 변형이 크게 발생하는 요소는 오일러 방법으로 정의하여 유한요소 격자망의 과도한 일그러짐 발생을 억제하고 재료 경계면에서의 거동을 추적할 수 있게 한다.
3. CEL 기법을 활용한 유한요소해석 모델의 극한 파괴 상태 기준 제시
3.1 비배수 상태의 지반 위에 놓인 연속기초(Strip Footing)의 극한 지지력 산정 문제
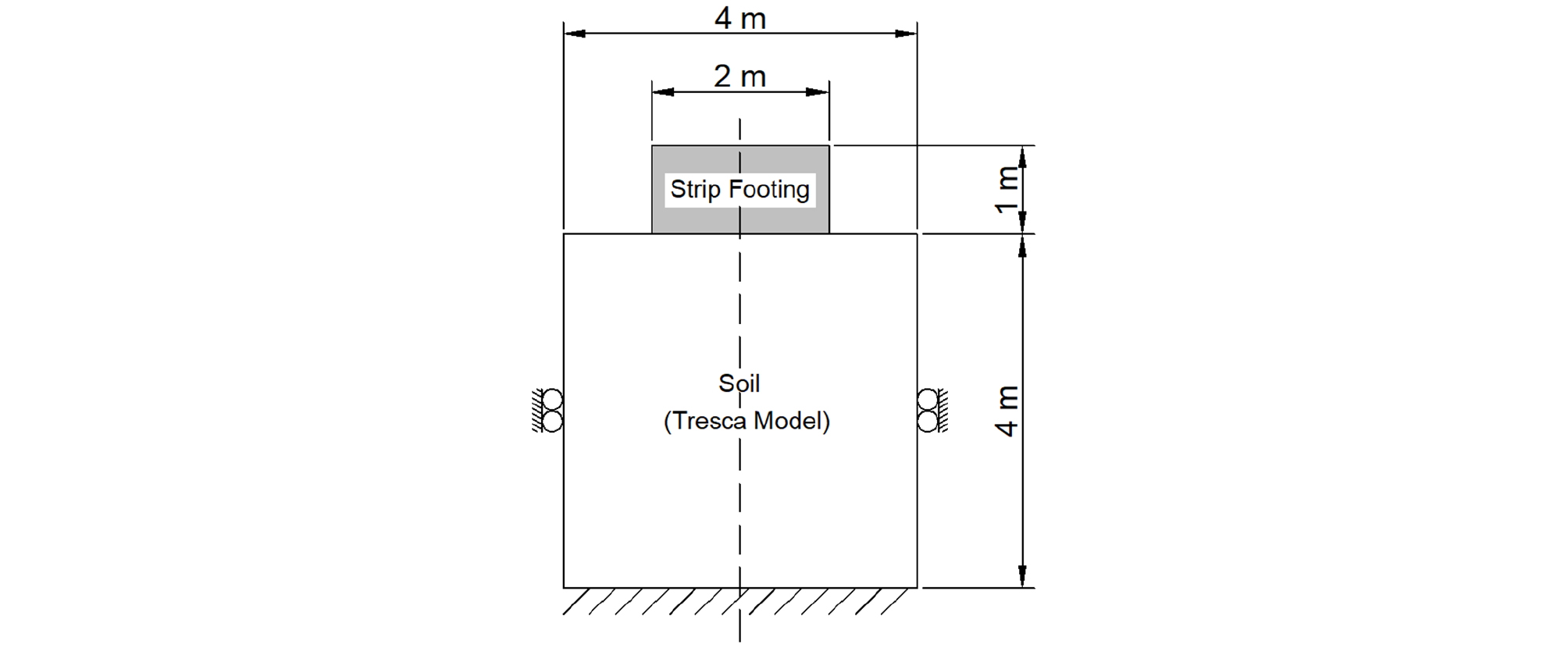
지반의 극한 파괴 상태를 정량적으로 감지할 수 있는 물리량 기준을 설정하기 위해 정확한 이론해가 존재하는 연속기초 문제를 선정하였다. Fig. 1에 보인 바와 같이 평면 변형률 조건에서 지반 영역은 폭 4m, 높이 4m이며, 기초는 폭 2m, 높이는 1m로 설정하였다. 지반은 전체 영역에서 하나의 비배수 전단강도를 가지는 비배수 상태에 놓인 점성토로 가정하였으며 자중은 고려하지 않았다. 대상 지반의 비배수 전단강도는 10kPa로 가정하였다. 비배수 상태의 점성토 거동을 모사하기 위해 Tresca 모델을 사용하였다. Tresca 모델에서 이러한 지반상태를 모사하기 위해 내부마찰각 는 0, 점착력 c는 10kPa로 설정하였다. 재료 모델에 필요한 물성치를 Table 1에 정리하였다.
Table 1. Material properties of strip footing model
| Property |
Young's modulus, E (kPa) | Poisson's ratio, ν | Friction angle, (°) |
Dilation angle, ψ (°) |
Cohesion, c (kPa) |
| Value | 2980 | 0.49 | 0 | 0 | 10 |
자중의 영향이 없는 비배수 상태의 점성토 지반 위에 연속기초가 놓이게 되면 Hill(1950)의 파괴 전단면 이론(Slip Line Theory)을 이용하여 기초의 최대 관입 압력(Maximum Punch Pressure), 즉 기초의 극한 지지력을 다음 식 (1)로 표현할 수 있다.
| $$\mathrm p=(2+\pi)c_u$$ | (1) |
여기서, p는 최대 관입 압력, cu는 비배수 전단강도이다. Table 1에서 비배수 전단강도 cu를 10kPa로 정하였으므로
| $$\mathrm p=(2+\pi)\times10=51.4\;\mathrm{kPa}$$ | (2) |
즉, 기초의 재하 하중이 51.4kPa에 도달하면 이론적으로 지반은 극한 파괴 상태에 도달한다.
3.2 CEL 모델링
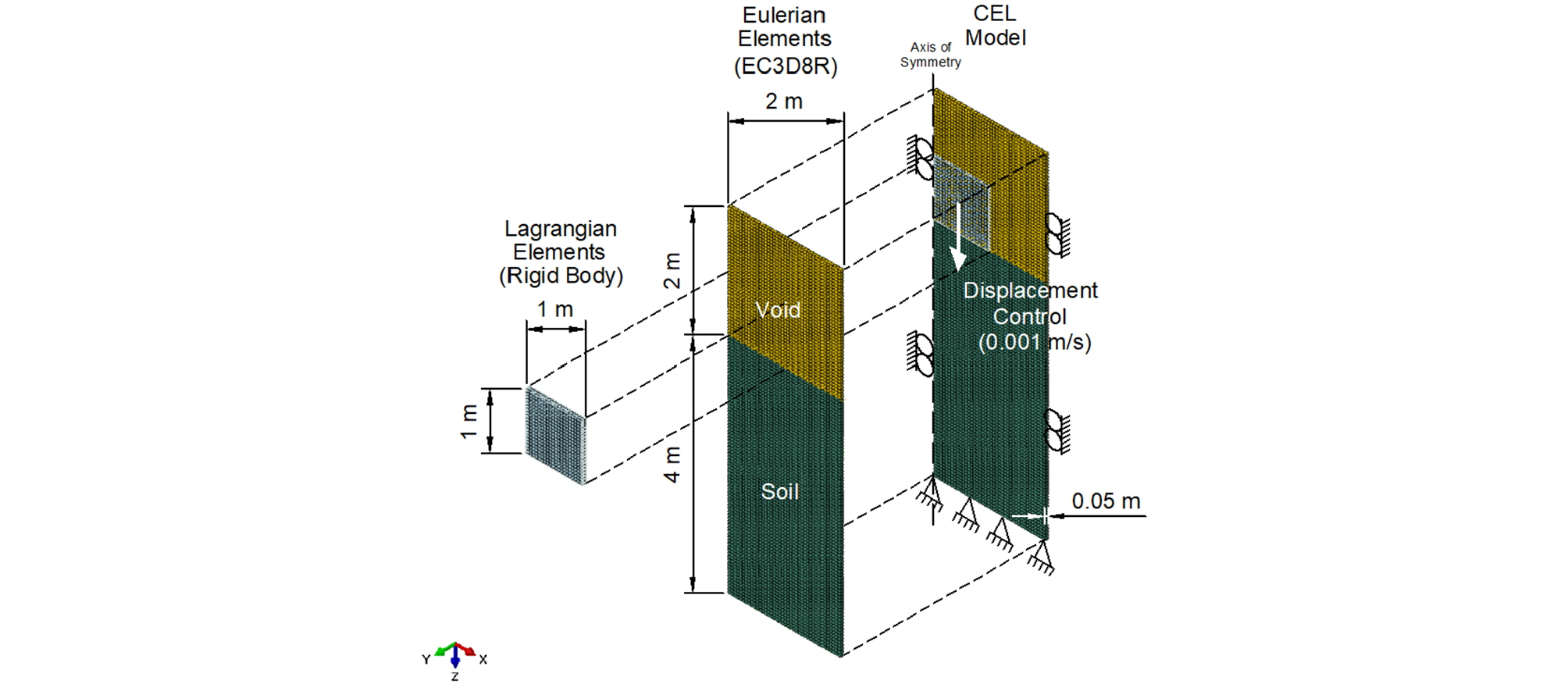
CEL 기법을 이용하여 연속기초 문제를 모델링하기 위해 상용 유한요소해석 프로그램인 ABAQUS/Explicit(2017)을 이용하였다. Fig. 2는 CEL 모델의 해석 영역과 경계조건을 보여준다. ABAQUS/Explicit(2017)에서 CEL 기법은 3차원 요소에 대해서만 제공되기 때문에 두께가 0.05m인 3차원 요소를 모델링한 후 평면 변형률 조건을 구현하기 위해 평면의 방향 축(y축)에 대해서 변위가 발생하지 않게끔 구속하였다. 해석 모델의 양 측면에서는 수평 변위를 구속하였다. 바닥면에서는 수평 및 연직 방향 변위를 모두 구속하였다.
CEL기법을 이용한 모델링에서 연속기초는 라그랑주 요소를 사용하여 강체로 모사하였다. 지반 영역은 오일러 요소를 사용하여 모사하였다. 여기서 오일러 요소는 지반 영역뿐만 아니라 지표면 위의 영역도 함께 모델링하여, 연속기초가 지반 내부로 관입되는 과정에서 지반 재료의 질점(Material Points)이 충분히 이동할 수 있도록 하였다. 해석 영역의 모든 요소는 평면 변형률 조건의 평면상에서 0.05m × 0.05m의 정사각형이 되도록 구성하였다.
라그랑주 요소로 모델링한 연속기초와 오일러 요소로 모델링한 지반 사이의 접촉 조건(Contact Condition)은 기초 저면과 지반 사이의 거친 접촉면(Rough Contact), 기초 측면과 지반 사이의 무마찰 접촉면(Frictionless Contact)으로 모델링하였다.
기초를 0.001m/s의 속도로 150초 간 총 0.15m를 지반 내에 관입시키면서 관측된 기초의 반력을 3.1절에서 계산된 극한지지력 51.4kPa과 비교하였다. 지반의 극한 파괴 상태 도달 시점을 감지할 수 있는 정량적인 물리량을 찾기 위해, 지반 영역에 대한 최대 소성 전단변형률과 최대 전단응력을 관측하였으며, 해석 시간에 따른 총 에너지, 내부 에너지, 운동 에너지, 소성 소산 에너지의 양과 변화속도를 조사하였다.
3.3 해석 결과
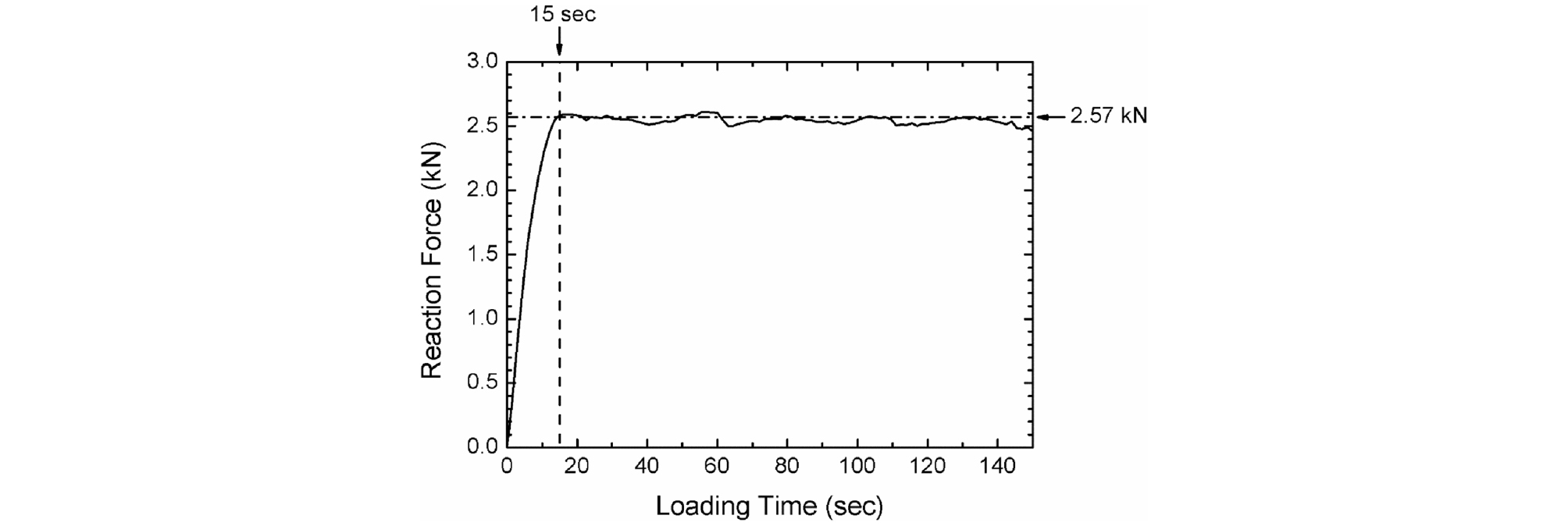
Fig. 3은 관입 재하 중 해석 시간에 따라 얻은 기초 반력의 변화를 보여준다. 앞서 설명한 바와 같이 기초의 단면적은 폭 1m × 두께 0.05m = 0.05m2이다. 따라서 Hill의 이론식에 의해 계산된 극한 지지력은 51.4kPa × 0.05m2 = 2.57kN이다. Fig. 3에 보인 바와 같이 기초의 반력이 2.57kN에 도달하면 반력의 크기가 더 이상 증가하지 않으며 계산된 극한 지지력의 수준을 유지하는 것을 확인할 수 있다. Fig. 3에서 알 수 있듯이 지반이 극한 파괴 상태에 도달하는 재하 시점은 15초이다.
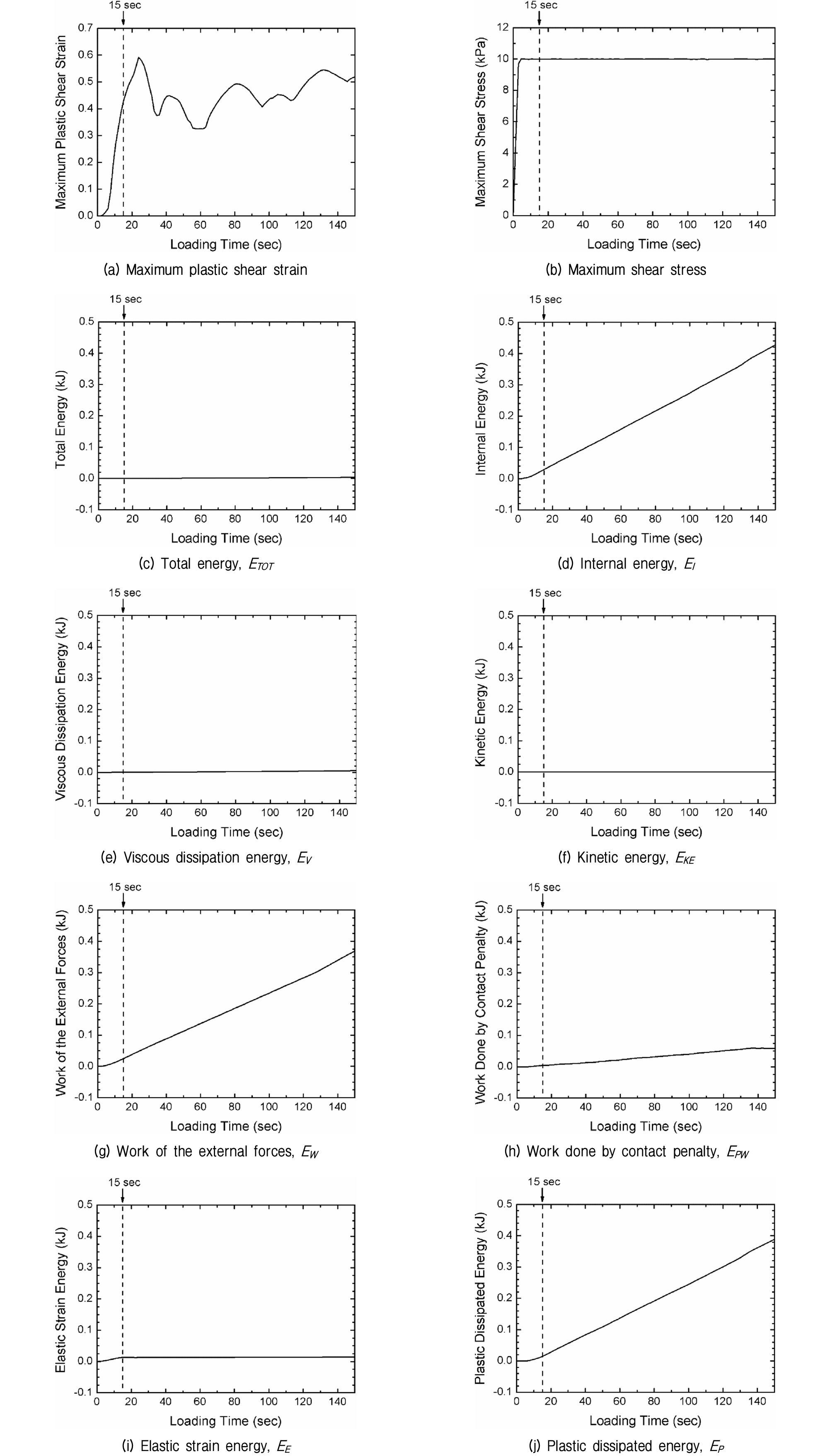
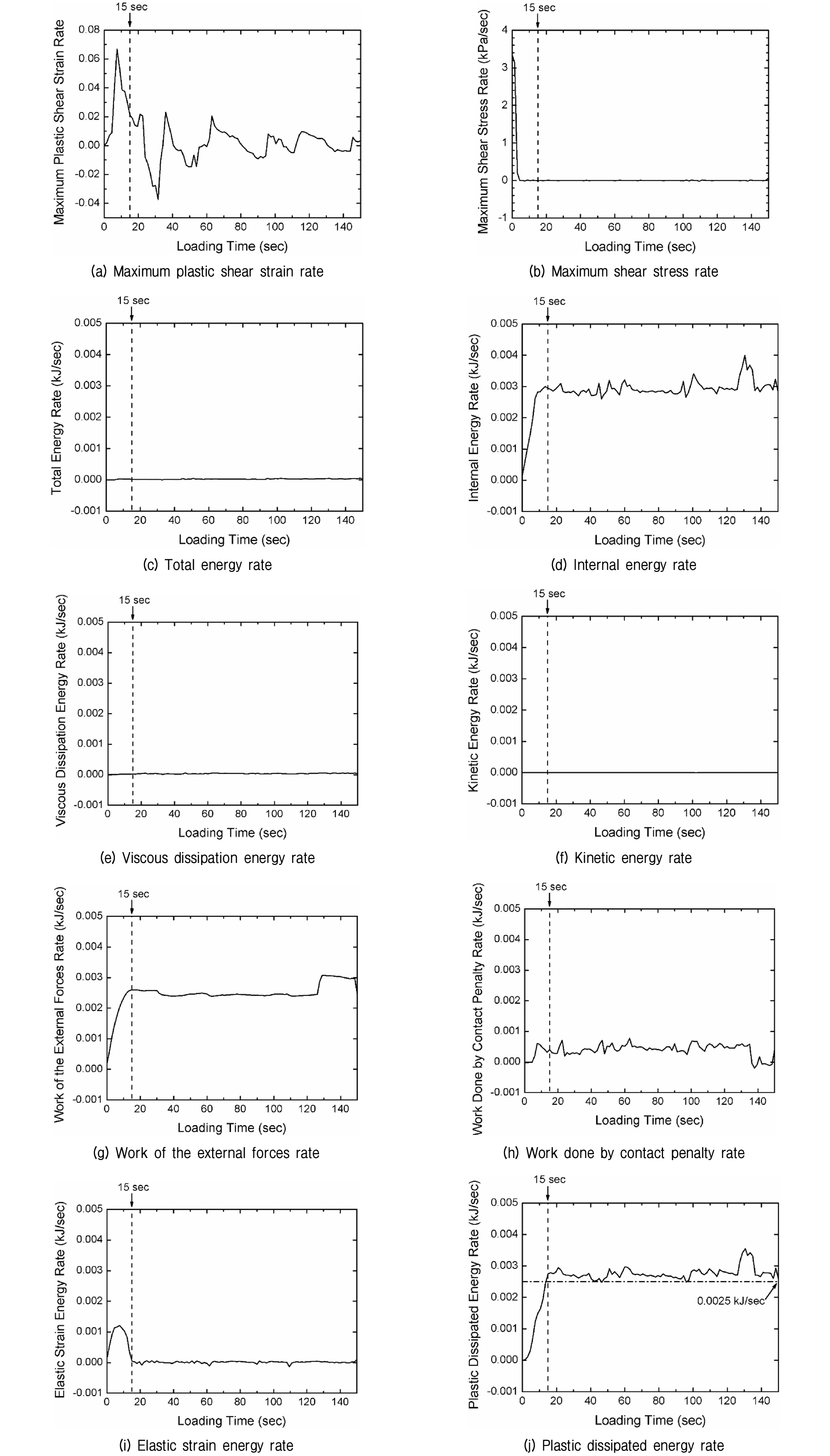
이론적으로 소성 전단 파괴가 시작되는 시점(즉, 재하 시점 15초)에서 특정 물리량이 급격하게 변화한다면, 그 물리량을 극한 파괴 상태를 판단할 수 있는 기준으로 정할 수 있다. Fig. 4는 전체 해석 영역에 대해서 재하 시간에 따른 최대 소성 전단변형률(Maximum Plastic Shear Strain), 최대 전단응력(Maximum Shear Stress), 총 에너지(Total Energy), 내부 에너지(Internal Energy), 재료의 점성에 의해 소산된 에너지(Viscous Dissipation Energy), 운동 에너지(Kinetic Energy), 외력에 의한 일(Work of the External Forces), 접촉 페널티에 의한 일(Work Done by Contact Penalty), 탄성 변형률 에너지(Elastic Strain Energy), 소성 소산 에너지(Plastic Dissipated Energy)의 변화를 보여준다. Fig. 4(a)에서는 최대 소성 전단변형률이 재하 시간 24초까지 선형적으로 증가하는 양상을 보였다. Fig. 4(b)에서 최대 전단응력은 재하 시간 3초가 되면 10kPa에 도달하였고 이후 일정한 값을 유지하였다.
본 해석 문제에서 에너지 평형 상태는 다음과 같이 표현할 수 있다.
| $$E_{TOT}=E_I+E_V+E_{KE}-E_W-E_{PW}$$ | (3) |
여기서, ETOT는 총 에너지(Total Energy), EI는 내부에너지(Internal Energy), EV는 재료의 점성에 의해 소산된 에너지(Viscous Dissipation Energy), EKE는 운동에너지(Kinetic Energy), EW는 외력에 의한 일(Work of the External Forces), EPW는 접촉 페널티에 의한 일(Work Done by Contact Penalty)이다. 각 에너지들의 정의는 다음과 같다.
| $$E_I=\int_0^t\left(\int_V\;\;\underset={\sigma^I}\;:\;\underset={\dot\varepsilon}dV\right)\mathrm{dt}$$ | (4) |
| $$E_V=\int_0^t\left(\int_V\;\;\underset={\sigma^V}\;:\;\underset={\dot\varepsilon}dV\right)\mathrm{dt}$$ | (5) |
| $$E_{KE}=\int_0^t\left(\int_V\;\;\rho\underline v\cdot\underline v\;dV\right)\mathrm{dt}$$ | (6) |
| $$E_W=\int_0^t\left(\int_S\;\;\underline v\cdot\underline{t^W}\;dS+\int_V\;\;\underline f\cdot\underline v\;dV\right)\mathrm{dt}$$ | (7) |
| $$E_{PW}=\int_0^t\left(-\int_S\;\;\underline v\cdot\underline{t^{PW}}\;dS\right)\mathrm{dt}$$ | (8) |
여기서, 는 내부 응력 텐서(Internal Stress Tensor), 는 변형률 속도 텐서(Strain Rate Tensor), 는 점성 응력 텐서(Viscous Stress Tensor), ρ는 질량 밀도, v는 속도 벡터, tW는 표면에 작용하는 분포 하중 벡터(Surface Distributed Load Vector), f는 체적력 벡터(Body Force Vector), tPW는 접촉 페널티 트랙션 벡터(Contact Penalty Traction Vector), t는 시간, V는 체적, S는 표면적을 의미한다.
에너지 평형 조건에 의해서 총 에너지, ETOT는 상수에 가깝게 크게 변화하지 않아야 한다. Fig. 4(c)에 보인 바와 같이 ETOT의 변화폭은 0∼4J로 매우 작은 값이며 수치 오차를 고려한다면 에너지 평형 상태를 만족한다 할 수 있다. 재료의 점성에 의해 소산된 에너지, EV와 운동 에너지, EKE의 크기 변화 역시 상대적으로 매우 작으며, 접촉 페널티에 의한 일, EPW가 0∼0.05kJ로 소폭 증가하는 양상을 보인다. 반면 내부에너지, EI와 외력에 의한 일, EW는 0∼0.4kJ로 눈에 띄게 증가하였다. 해석 결과를 종합해보면 외력에 의한 일과 접촉 페널티에 의한 일이 내부에너지로 전환되어 에너지 평형 상태가 유지됐다고 볼 수 있다.
본 해석 문제에서 내부에너지, EI는 다음과 같이 표현할 수 있다.
| $$E_I=E_E+E_P$$ | (9) |
여기서, EE는 탄성 변형률 에너지(Elastic Strain Energy), EP는 소성 소산 에너지(Plastic Dissipated Energy)를 의미한다. 탄성 변형률 에너지와 소성 소산 에너지의 정의는 다음과 같다.
| $$E_E=\int_0^t\left(\int_V(1-d)\underset={\sigma^u}:\underset={\varepsilon^{\dot el}}\;dV\right)\mathrm{dt}$$ | (10) |
| $$E_P=\int_0^t\left(\int_V(1-d)\underset={\sigma^u}:\underset={\varepsilon^{\dot el}}\;dV\right)\mathrm{dt}$$ | (11) |
여기서, d는 연속체 손상 계수(Continuum Damage Parameter), 는 비손상 응력 텐서(Undamaged Stress Tensor), 는 탄성 변형률 속도 텐서(Elastic Strain Rate Tensor), 는 소성 변형률 속도 텐서(Plastic Strain Rate Tensor)를 의미한다.
지반이 극한 파괴 상태에 도달하면 내부에너지는 대부분 비탄성 소산 에너지 즉, 소성 소산 에너지가 차지하게 된다. Fig. 4(d)와 Fig. 4(j)를 비교해보면 내부에너지 EI와 소성 소산 에너지 EP의 크기와 변화 양상이 거의 유사한 것을 확인할 수 있다. 재하시간에 따른 각종 물리량의 변화에서는 재하시간 15초 전후에서 확연한 차이가 나타나는 특이한 물리량의 변화는 찾기 어렵다.
Fig. 5는 Fig. 4에 제시한 물리량들을 시간에 대해 미분하여 물리량의 변화속도를 정리한 그림이다. Fig. 5(j)에 도시한 바와 같이 소성 소산 에너지, EP의 변화속도가 재하시간 15초 전후에서 가장 뚜렷한 차이를 보였으며 이때의 소성 소산 에너지의 변화속도는 0.0025kJ/sec이다. 해석 결과를 바탕으로 본 연구에서는 지반의 극한 파괴 상태를 감지할 수 있는 물리량 기준을 다음과 같이 설정하였다.
| $$\frac{dE_P}{dt}>0.0025\;kJ/sec\;(Ultimate\;Failure\;Condition)$$ | (12) |
3.4 설정된 물리량 기준의 적합성 검증
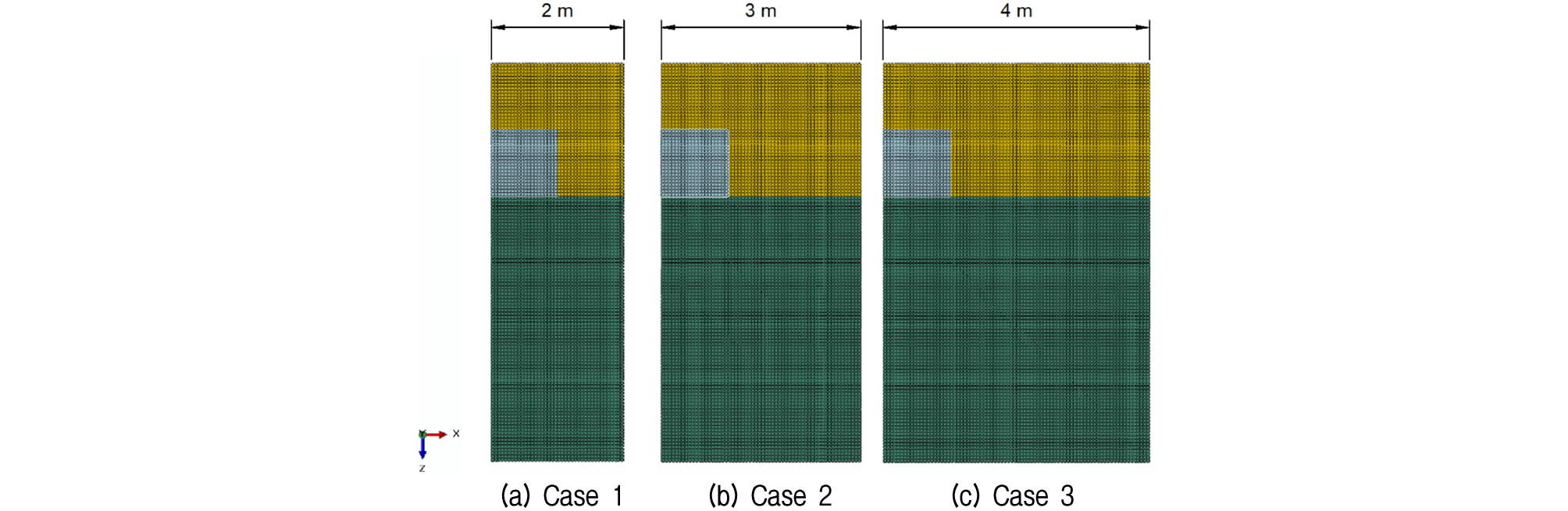
서로 다른 해석 조건에서 지반이 극한 파괴 상태가 될 때에 본 연구에서 제시한 물리량이 정량적으로 일정하게 감지가 된다면 기준으로써 적합하다고 할 수 있다. 설정된 물리량 기준의 적합성을 검증하기 위해 해석 조건을 다르게 설정하여 해석 결과를 비교 검토하였다. Table 2와 Fig. 6은 해석 조건을 보여준다. 오일러 방법으로 모델링한 지반 요소의 폭을 2m, 3m, 4m의 총 3가지로 서로 다르게 설정하여 결과를 비교 분석하였다. 지반 요소의 폭을 제외한 모든 해석 조건은 3.2 절의 해석 모델과 동일하다.
Table 2. Analysis conditions of the strip footing model
| Cases | The total width of analysis model |
| Case 1 | 2 m |
| Case 2 | 3 m |
| Case 3 | 4 m |
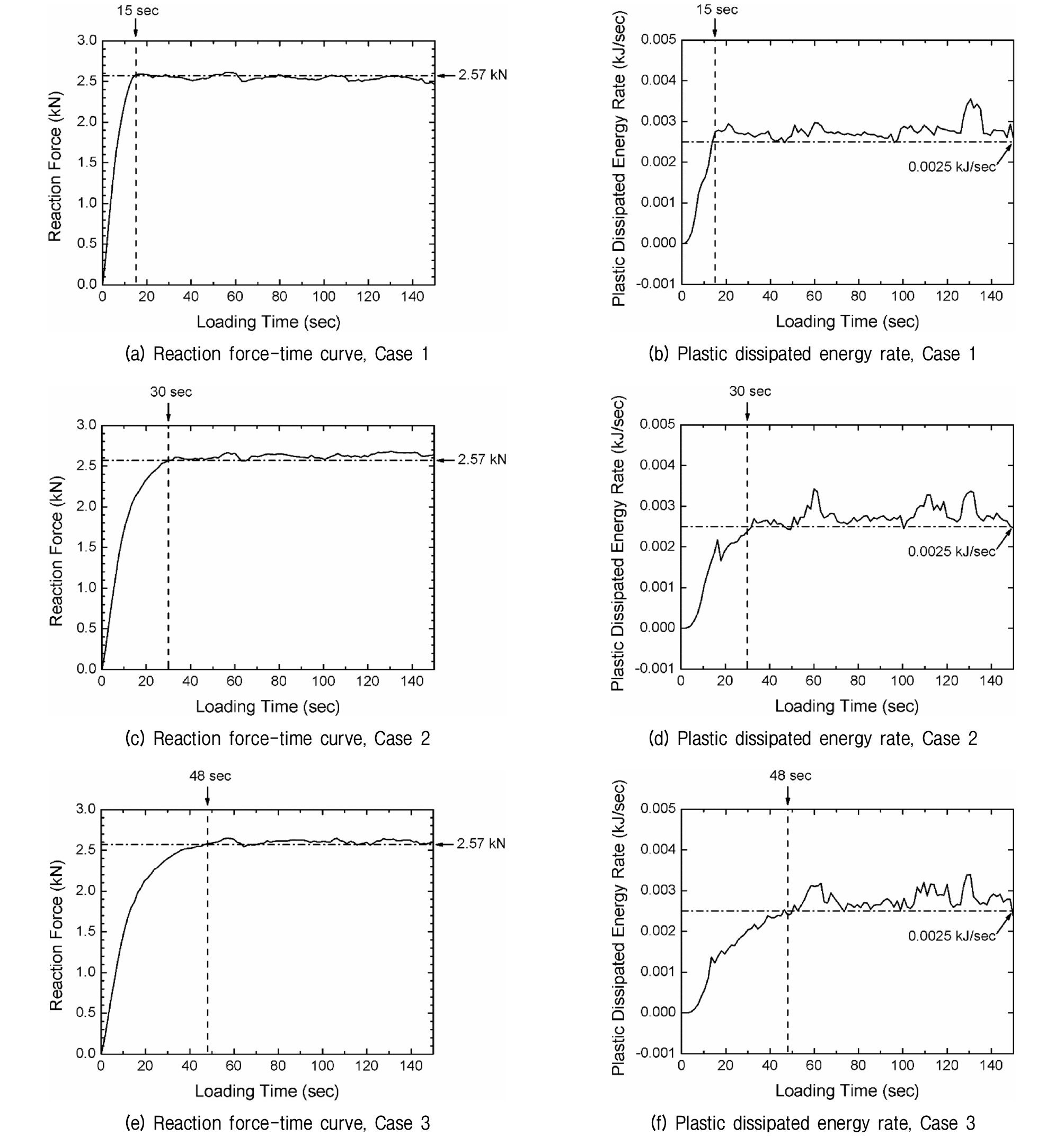
Fig. 7(a), Fig. 7(c), Fig. 7(e)는 해석 조건에 따른 시간 대비 기초의 반력을 보여준다. 모든 해석 조건에서 기초의 반력이 지반의 이론적 극한 지지력인 2.57kN에 도달하면 기초 반력의 크기는 크게 변화하지 않으며 현재의 하중 수준을 유지하는 경향을 나타낸다. 지반 요소의 폭이 증가함에 따라 극한 지지력에 도달하는 시점 즉, 소성 전단 파괴가 시작되는 시점이 늦어진다. Case 1은 재하시점 15초, Case 2는 30초, Case 3는 48초에서 소성 전단 파괴가 나타났다.
Fig. 7(b), Fig. 7(d), Fig. 7(f)는 해석 조건에 따른 시간 대비 소성 소산 에너지의 변화속도를 보여준다. 모든 해석 조건에서 소성 전단 파괴가 일어나는 시점, 즉 15초, 30초, 48초일 때 소성 소산 에너지의 변화속도가 동일하게 0.0025kJ/sec로 측정되었다. 모든 해석 조건이 본 연구에서 설정한 물리량 기준을 만족하므로, 극한 파괴 상태를 감지하는 기준으로 소성 소산 에너지의 변화속도가 적합한 물리량이라 할 수 있다.
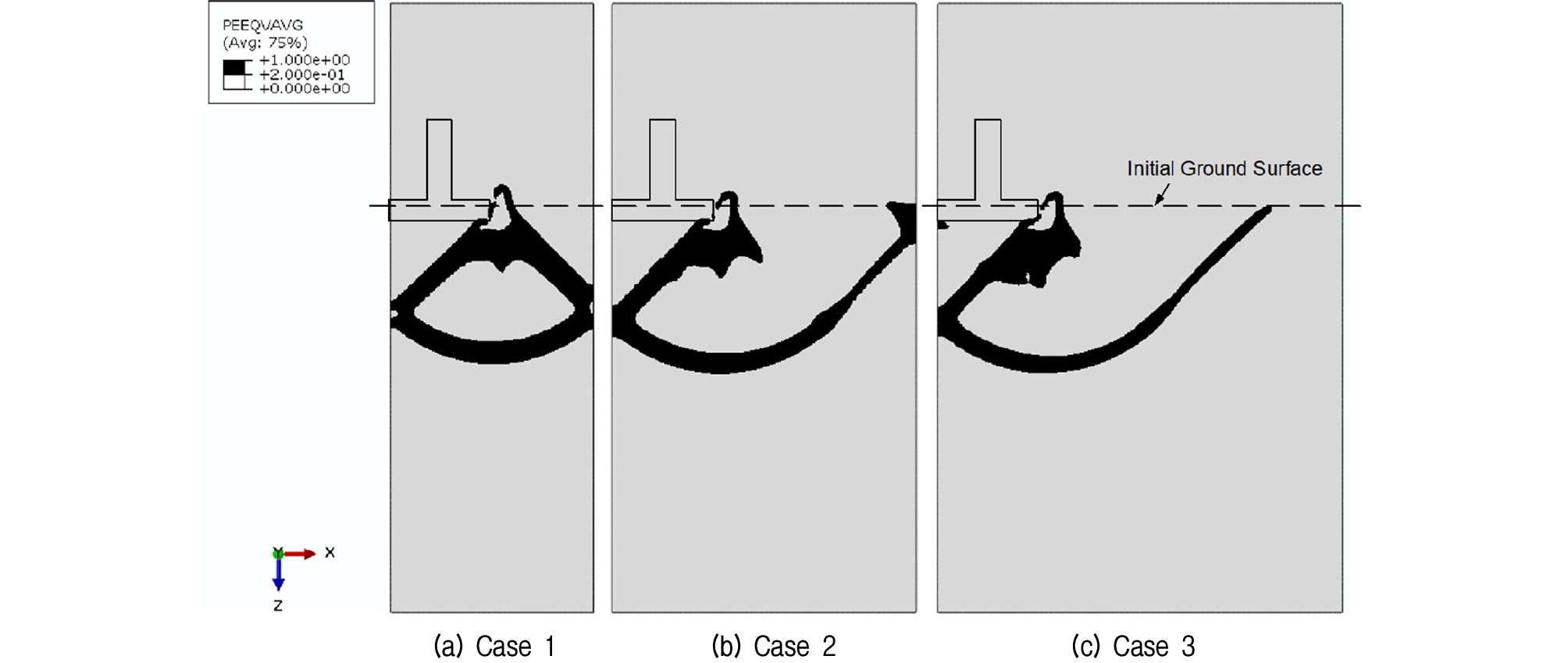
본 해석 모델의 결과를 이용하여 일반적인 지반 구조물 설계에 필요한 파괴 전단면을 손쉽게 확인할 수 있다. Fig. 8은 각 조건에서 기초의 재하가 완료되었을 때 등가 소성 변형률(Equivalent Plastic Strain)의 분포를 보여준다. 검은색으로 표시된 영역은 등가 소성 변형률의 20% 이상 소성 변형이 일어난 영역이다. Fig. 8에서 파괴 전단면을 확인할 수 있으며, 해석 영역이 넓어짐에 따라 파괴 전단면의 진전 양상을 파악할 수 있다.
4. 결 론
본 연구에서는 CEL 기법을 이용한 유한요소해석 모델에서 지반의 극한 파괴 상태를 감지할 수 있는 정량적 물리량 기준을 제시하기 위해 수치해석을 실시하였다. 정확한 이론해가 존재하는 연속기초의 극한 지지력 산정 문제를 CEL 기법으로 해석하였으며 다양한 물리량이 극한 파괴 상태에서 어떻게 변화하는지 관측하고 분석하였다. 최대 소성 전단변형률, 최대 전단응력, 총 에너지, 내부 에너지, 운동 에너지, 소성 소산 에너지의 시간에 따른 변화를 관측하였으며 관측된 물리량의 변화속도를 비교 검토하였다. 여러 물리량 가운데 소성 소산 에너지의 변화속도가 소성 전단 파괴가 시작되는 시점에서 뚜렷하게 변화하는 것을 확인하였다. 해석 결과를 바탕으로 본 연구에서는 소성 소산 에너지의 변화속도가 0.0025kJ/sec를 넘어서면 지반이 극한 파괴 상태가 된다는 물리량 기준을 제시했다. 지반의 폭이 2m, 3m, 4m인 총 3가지의 해석 조건에 대해서도 동일한 기준에 의해 지반의 극한 파괴 상태를 감지할 수 있음을 확인하였다.