1. 서 론
잔교식 안벽은 말뚝으로 지지되는 항만 구조물로서 항만 화물의 운송에 이용되는 중요 구조물이다. 잔교식 안벽은 화물 운송을 위한 상판을 수심이 깊은 해상까지 연결하고, 이 상판은 말뚝구조물로 지지된다. 잔교식 안벽의 일반적인 형태는 말뚝 또는 기둥(column)으로 지지되는 상판(deck), 뒤채움을 위한 옹벽 및 제방으로 구성되며, 때로는 횡방향력에 효과적으로 저항하기 위해 경사말뚝을 설치하기도 한다.
그런데, 잔교식 안벽을 지지하는 말뚝기초는 수심을 확보하기 위하여 일반적으로 경사지반에 설치되며, 파압, 접안하중 그리고 지진 등 복잡한 하중조건을 받는다. 이러한 다양한 설계조건에 대한 말뚝의 거동을 분석하기 위하여 지반-말뚝 상호작용을 적절히 모사하는 것이 필요하다. 실무적으로 지반-말뚝 상호작용은 정적 또는 반복수평 하중실험 결과를 근거로 제시된 p-yp 곡선(p=지반의 비선형 수평저항력, yp=말뚝의 변위)으로 모사하고 있다(Matlock and Reese, 1960; Matlock, 1970; Reese and Welch, 1975; API, 2000).
그런데, 대부분의 p-yp 곡선은 정적인 하중 조건에서 제안되었기 때문에 지진과 같은 동적하중을 받는 말뚝조건에 적용하기 어렵다. 그러므로, 일부 연구자들이 동적 원심모형실험 등을 수행하여 동적 p-y 곡선(y=말뚝과 지반의 상대변위)을 제안한 바 있다(Yang et al., 2011; Yoo et al., 2013; Choi et al., 2015; Nguyen et al., 2018). 동적 p-y 곡선은 기존의 p-yp 곡선과 비교하여 지진하중을 받는 말뚝의 거동을 합리적으로 모사할 수 있다. 그러나, 대부분의 실험이 수평지반 조건에 대하여 수행되었으며, 항만 잔교식 안벽을 지지하는 말뚝과 같이 경사지반에 대한 p-y 곡선 그리고 개별말뚝 사이의 동적 상호작용 등에 대한 연구는 아직 미흡하다.
또한, 지진하중을 받는 말뚝은 Fig. 1과 같이 상부구조물의 관성력(inertia force)과 지반변위에 의한 운동학적 힘(kinematic force)의 영향을 모두 받는다.
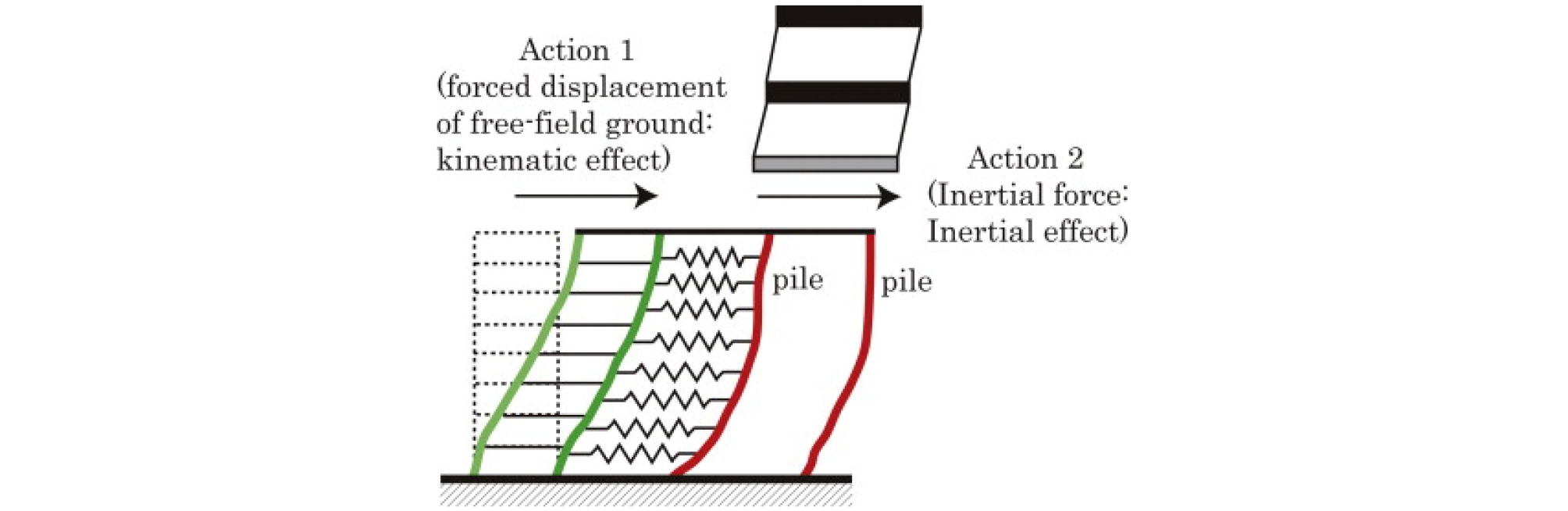
Fig. 1.
Inertial and kinematic forces acting on piles under dynamic loading (adopted from Kojima et al., 2014)
관성력과 운동학적 힘의 상호작용은 구조물의 강성, 지반 물성값 그리고 입력파의 특성 등에 의해 영향을 받을 수 있다. Kim et al.(2004)는 중력식 안벽에 대한 1-g 진동대 실험을 수행하여 벽체에 작용하는 하중 성분 사이의 위상관계를 분석한 바 있다. 그 결과 벽체의 관성력과 동적 토압은 초기에 관성력과 180° 위상차를 보이지만 배면지반 내 과잉간극수압이 증가하면서 배면지반이 연약해지면 동적 토압이 관성력과 동일한 위상으로 변하는 것을 관찰하였다. Nakamura(2006), Al Atik and Sitar(2010), and Shin et al.(2019)도 벽체의 최대 관성력과 배면 동적 토압 사이에 위상 차이가 존재한다고 제시하였다.
이 후 Yoo et al.(2017) 등은 일련의 원심모형실험을 수행하여 지진하중을 받는 단일말뚝의 관성력과 운동학적 힘에 대하여 연구하였다. 그 결과, 상부구조물의 관성력에 의한 말뚝 변위와 지반변위에 의한 운동학적 힘은 초기에는 반대 위상이었지만 지반 액상화가 발생한 이후에는 동일한 위상으로 변하는 것을 관찰하였다. 이는 이전의 연구자들이 중력식 안벽에서 관찰한 벽체 관성력과 배면 토압 사이의 위상변화와 동일한 경향이다.
지진하중을 받는 무리말뚝을 대상으로 관성력과 운동학적 힘의 상관관계를 분석한 연구는 매우 부족한 실정이다. 그러므로, 본 연구에서는 경사지반에 설치된 단일말뚝과 무리말뚝에 대하여 동적원심모형실험을 수행하고, 말뚝의 동적 p-y 곡선 및 말뚝의 관성력과 운동학적 힘의 상호작용을 분석하였다. 단일말뚝과 2열×2행 무리말뚝을 동일한 토조에 함께 설치하였으며 경사지반은 건조 실리카 모래로 조성하였다. 그리고, 상부 구조물의 관성력을 모사하기 위하여 말뚝 두부에 알리미늄 상판을 고정하였다. 관성력과 운동학적 힘의 상호작용은 상판의 변위와 토조 변위의 위상관계를 이용하여 분석하였다. 그리고, 말뚝의 휨모멘트와 지반 가속도 측정결과를 이용하여 동적 p-y 곡선을 산정하고 경사지반 및 무리말뚝 효과가 말뚝-지반 상호작용에 미치는 영향을 분석하였다.
2. 원심모형실험 프로그램
본 실험은 한국과학기술원(KAIST)에서 보유하고 있는 원심모형실험 시설을 이용하였다. 본 시험기의 회전 반경은 5m, 최대 원심력은 240 g-ton을 가할 수 있다. 실험에 적용된 원심가속도는 34g로서 이는 모형과 원형 사이의 길이 상사비 34에 해당한다. 모형체 제작을 위하여 Wood(2004)와 Madabhushi(2014)가 제안한 상사법칙을 적용하였다. 본 논문에서 표시한 단위는 모두 상사법칙을 적용하여 원형구조물의 값으로 환산하여 표기하였다.
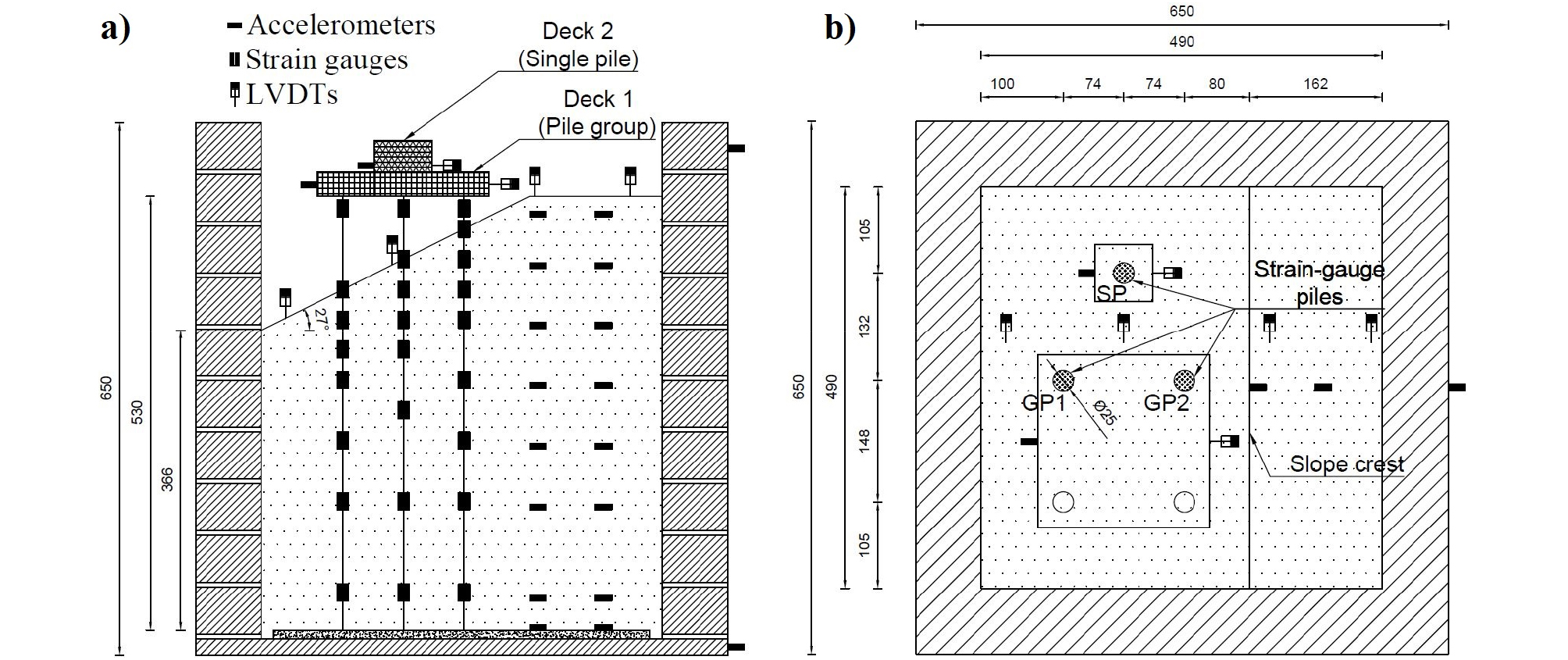
Fig. 2는 원심모형실험 단면으로서 동일한 토조 내에 2열×2행의 무리말뚝과 단일말뚝을 함께 설치하였다. 지반은 건조 실리카 모래로서 지반 경사는 27°이다. 모형 말뚝은 알루미늄 관으로 제작하였으며, 제원은 외경 25mm, 두께 2mm, 길이 530mm이며 상사법칙을 적용한 원형말뚝의 치수는 외경 0.85m, 두께 68 mm, 길이 18m에 해당한다. 본 연구는 횡방향 지진력에 대한 말뚝의 휨강성이 중요하므로 휨강성에 대한 상사법칙을 적용하였다. 무리말뚝의 상판(Deck 1)은 현장 잔교식 안벽의 말뚝 1본 당 작용하는 하중을 고려하여 상판의 두께를 결정하였다. 상판(Deck 1)은 가로와 세로 각각 7.14m의 정방향 형상으로 두께는 1.97m이며, 밀도 2.69ton/m3의 알루미늄판을 이용하여 제작하였다. 단일말뚝의 상판(Deck 2)은 무리말뚝에 적용된 상판질량의 1/4을 적용하여 말뚝 1본당 작용하는 축하중은 동일하다. Table 1에 모형 말뚝과 상부구조물의 물성값을 정리하였다.
Table 1. Material properties of pile and deck (in prototype scale)
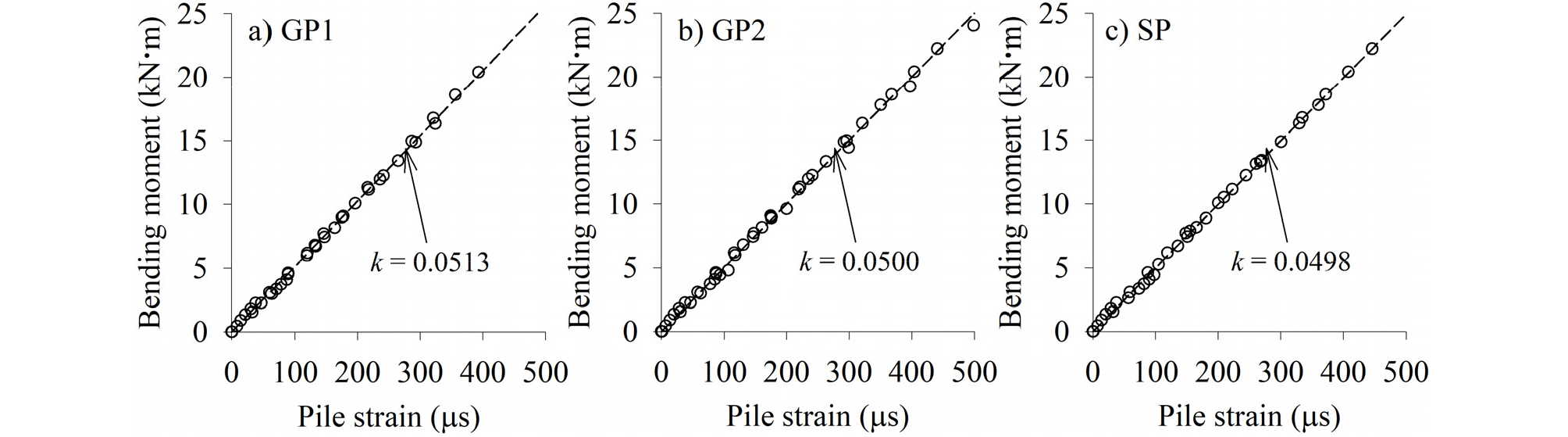
단일말뚝(SP)과 무리말뚝 중 2본(GP1, GP2)에 대하여 변형률계를 설치하여 휨모멘트를 측정하였다. 변형률계는 말뚝 당 8쌍 또는 9쌍을 설치하였다. 말뚝의 휨강성(EI)값은 개별 말뚝에 대해 Fig. 3과 같이 보정 실험을 수행하여 산정하였다. 말뚝 선단을 수평으로 고정한 상태에서 말뚝 머리에 무게추를 매달면서 휨모멘트를 증가시켰다. 이 때 말뚝에서 계측된 변형률과 이론적으로 계산된 휨모멘트 값의 관계를 이용하여 휨강성을 결정하였다.
실험에 사용한 토조는 ESB(Equivalent Shear Beam) 토조이다. ESB 토조는 강성링들 사이에 고무를 적층하여 제작한다. ESB 토조의 횡방향 강성은 지반의 강성과 유사하고 진동시 벽체의 횡방향 변위가 발생하므로 강성벽체와 흙 사이의 충돌에 의해 발생하는 반사파 및 교란효과를 감소시킨다. 토조의 크기는 모형스케일로 49cm(폭) × 49cm(길이) × 63cm(높이) 이다.
모형지반에 이용된 흙은 건조 실리카 모래로서 Table 2에 흙의 물성값을 정리하였다. 모형체 제작의 순서는 ① 말뚝 선단을 토조 바닥면에 회전 고정시킴, ② 건조 낙사법을 이용하여 낙사장치의 노즐폭, 모래낙하높이, 이동속도 등을 조정하면서 상대밀도 약 50%의 균일한 지반 조성, ③ 지반 조성 중 계획된 위치에 가속도계 설치, ④ 진공청소기로 모래를 흡입하여 경사지반 제작(경사=27°), ⑤ 상판과 말뚝 머리부의 회전구속 연결, ⑥ 변위계 설치 등의 순서로 진행하였다.
Table 2. Properties of model ground
| Properties | Values |
| Relative density (%) | 50.0 |
| Unit weight (kN/m3) | 13.94 |
| Internal friction angle (degree) | 38.0 |
| Specific gravity | 2.65 |
| Soil classification (USCS) | SP |
| Mean grain size D50 (mm) | 0.237 |
계측기는 말뚝체에 발생하는 휨모멘트 분포를 측정하기 위한 변형률계, 상판의 수평변위 및 지표면 침하를 계측하는 LVDTs, 그리고 지반의 깊이별 가속도 분포와 상판구조물의 가속도 측정을 위한 가속도계 등을 설치하였다. 특히, 말뚝 변형률계의 선은 말뚝 내부의 빈 공간을 통해 말뚝 머리로 빼내어 주변 흙에 미치는 영향을 제거하였다.
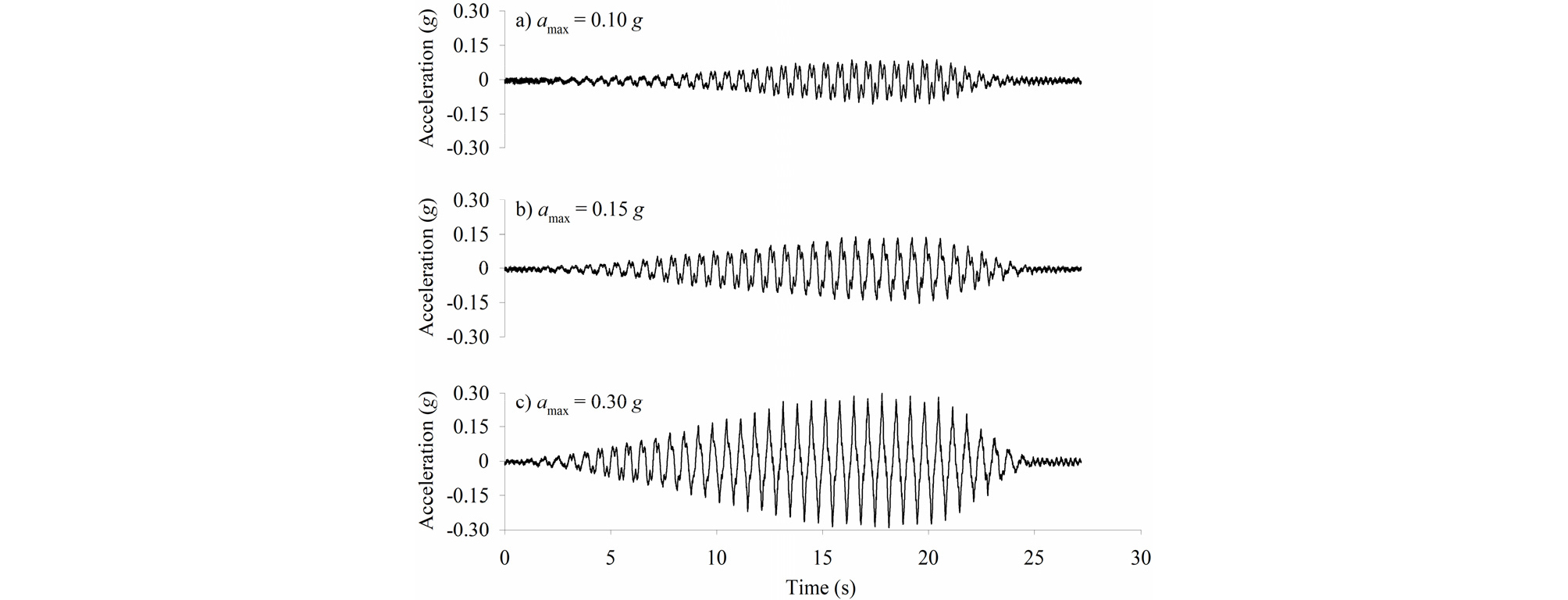
입력지진파는 Fig. 4와 같이 sine 파를 가하였는데 주파수 1.5Hz로 고정시킨 상태에서 진폭은 선형적으로 증가시켰다. 최대 가속도 진폭은 0.10g, 0.15g, 0.30g로 변화시키며 3가지 지진파를 순차적으로 가하였다. 지진하중 크기에 따른 말뚝거동 및 위상변화를 관찰하기 위해서 sine 파의 진폭을 선형적으로 증가시켰으며, sine 파의 주파수 1.5Hz는 일반적인 지진파의 주요 주파수 범위를 고려하여 결정하였다. Fig. 4는 실제 토조 바닥면에 입력된 지진파인데 가진 시스템의 특성에 의해 잡음 신호가 함께 입력되면서 완전한 sine 파형으로 가진되지 못하였다.
3. 실험 결과
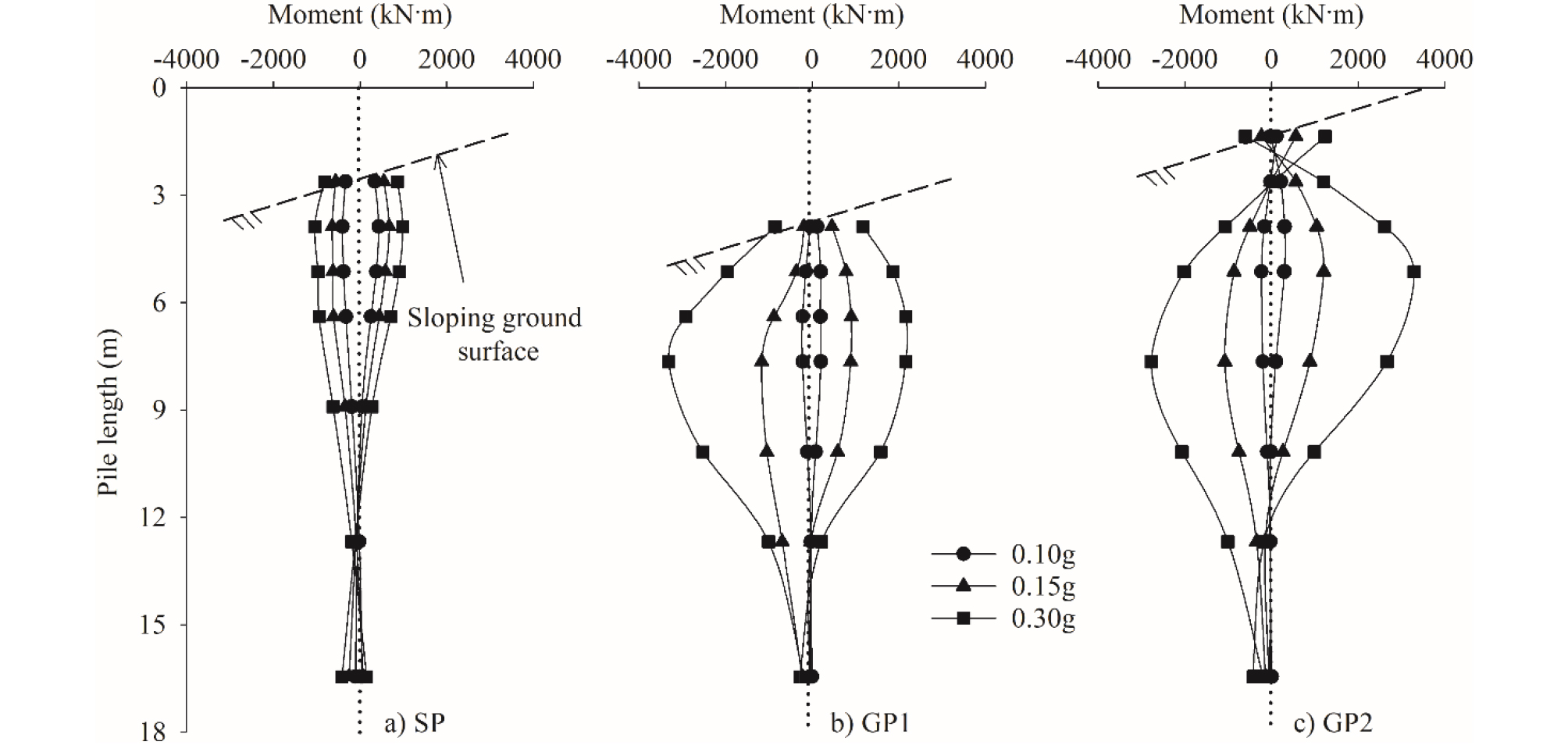
Fig. 5는 입력지진파의 최대진폭이 각각 0.10g, 0.15g, 0.30g일 때 단일말뚝과 무리말뚝의 최대 휨모멘트 분포곡선이다. 무리말뚝(GP1, GP2)의 최대 휨모멘트는 단일말뚝(SP)과 비교하여 진폭 0.10g, 0.15g, 0.30g에서 각각 평균 약 0.5배, 1.74배, 3.3배로 증가하였다.
입력가속도 진폭이 0.10g일 때 단일말뚝의 최대 휨모멘트가 무리말뚝의 약 2배로 증가한 이유는 무리말뚝의 경우 무리말뚝 배열에 의해 말뚝 두부의 회전발생이 크게 억제되지만 단일말뚝의 두부는 회전이 자유롭기 때문으로 판단된다. 그리고, 입력가속도 진폭이 0.15g와 0.30g로 증가하였을 때 무리말뚝의 휨모멘트가 단일말뚝에 비하여 각각 1.74배와 3.3배로 증가하였다. 무리말뚝의 휨모멘트가 크게 발생한 이유는 가속도 진폭이 커지면서 지반과 말뚝 사이의 운동학적 힘의 영향이 커졌고 그 영향이 단일말뚝과 무리말뚝에 서로 다르게 발생하였기 때문으로 판단된다.
말뚝과 지반 사이의 운동학적 힘은 지반과 말뚝 사이의 상대 변위 관계에 의해 발생한다. 진동 중 지반의 변위가 말뚝의 변위보다 크면 지반이 말뚝을 미는 하중을 발생시키고, 지반의 변위가 말뚝의 변위보다 작으면 지반이 말뚝을 지지하는 저항력을 발휘한다.
말뚝과 지반의 변위는 흙의 강성, 말뚝-구조물의 휨강성, 그리고 입력지진파의 크기 등 여러 가지 요인들에 의해 영향을 받는다. 본 실험에서는 말뚝의 변위는 상판의 변위와 직접적으로 비례하고 지반의 변위는 입력파의 변위에 비례하는 것으로 가정하였다. 그러므로, 말뚝과 지반 사이의 운동학적 상관관계를 분석하기 위하여 상판의 변위와 입력파 변위를 분석하였다.
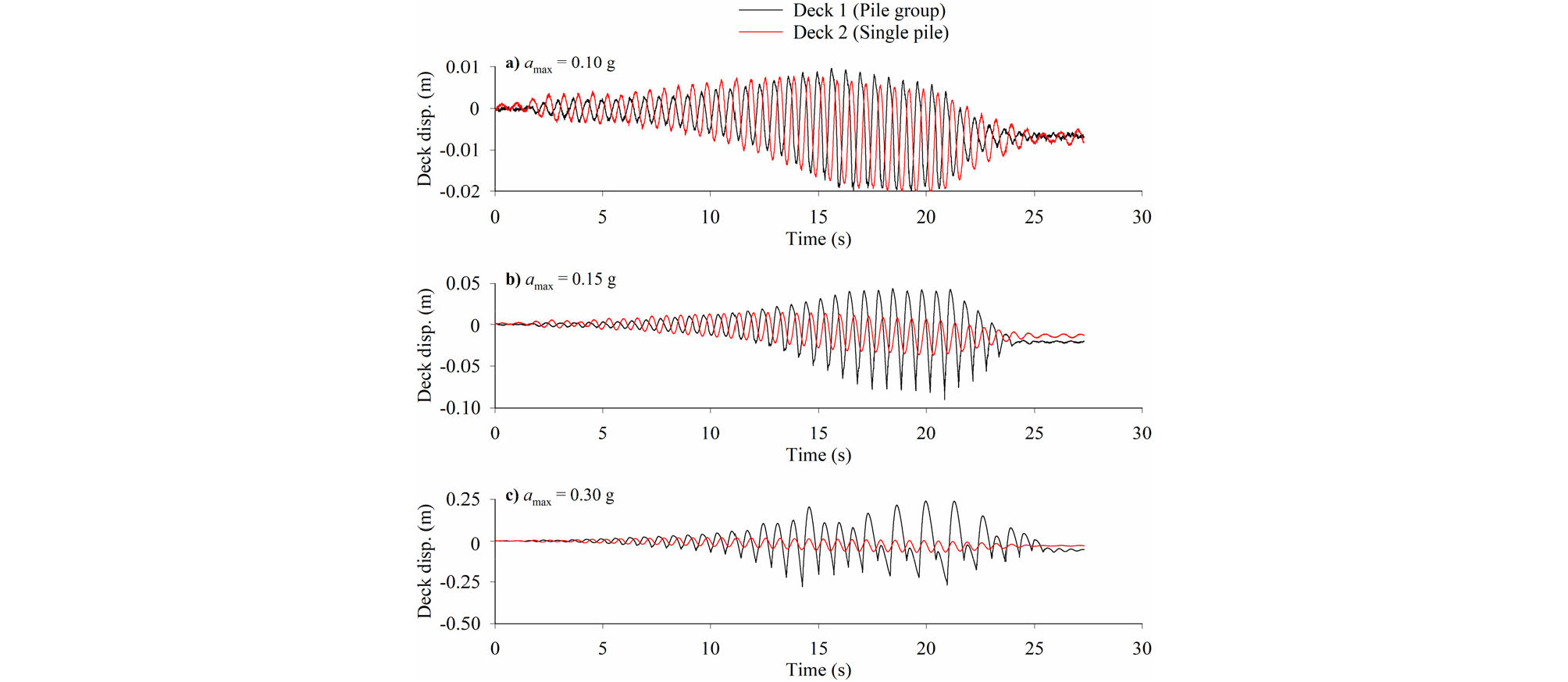
Fig. 6은 입력지진파 최대진폭이 각각 0.10g, 0.15g, 0.30g일 때 단일말뚝과 무리말뚝 상판의 변위 시간이력이다. 전체적인 경향을 보면 무리말뚝 상판과 단일말뚝 상판의 변위는 서로 반대의 위상차를 보여주고 있으며 입력가속도 진폭이 증가하면서 위상차가 점차 감소하였다. 그리고, 0.10g일 때 무리말뚝과 단일말뚝의 상판변위 진폭은 유사하지만 0.15g와 0.30g일 때 무리말뚝의 변위진폭이 단일말뚝보다 크게 증가하였다. Fig. 6(c)에서 무리말뚝 상판 변위 측정결과가 불규칙한 것은 관성력이 커지면서 무리말뚝 두부와 상판의 연결부가 일부 파손되었기 때문이다.
진동이 끝났을 때 경사지반의 측방변형에 의해 상판에 잔류변위가 발생하였다. 무리말뚝 상판(Deck 1)과 단일말뚝 상판(Deck 2)의 잔류변위는 0.10g일 때 각각 7mm와 8mm, 0.15g일 때 각각 21mm와 14mm, 그리고 0.30g일 때 52mm와 28mm 발생하였다. 즉, 0.10g일 때 무리말뚝의 잔류변위는 단일말뚝보다 1mm 작았지만, 0.15g와 0.30g일 때 무리말뚝의 잔류변위는 단일말뚝과 비교하여 평균적으로 각각 1.5배와 1.9배로 증가하였다.
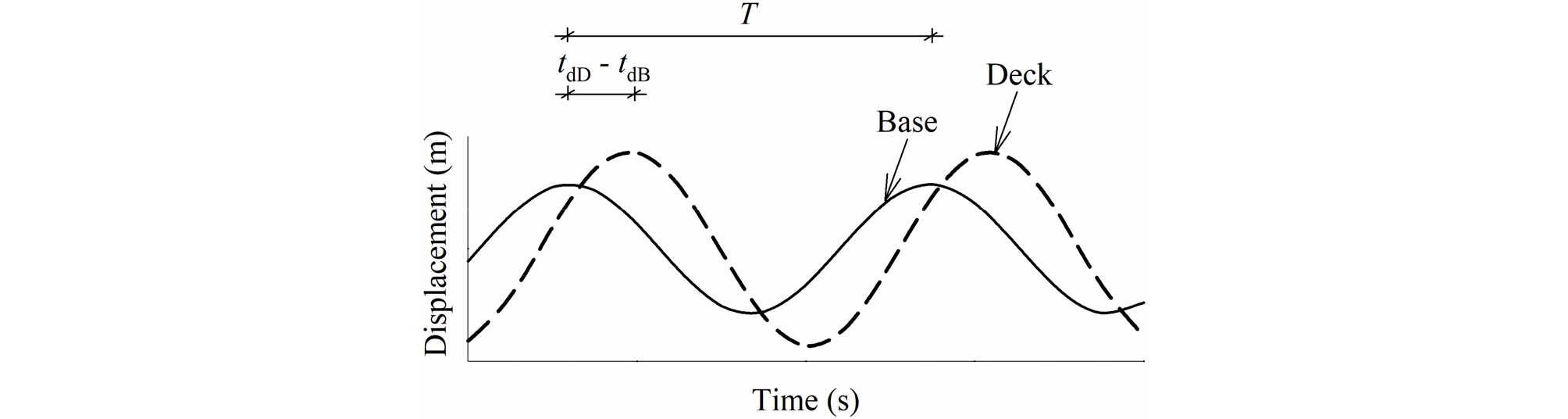
말뚝과 지반의 운동학적 상호작용를 분석하기 위하여 Fig. 6의 상판과 입력파 변위에 대한 위상관계를 분석하였다. Fig. 7은 변위 위상차에 대한 정의를 보여준다. 먼저, 입력파와 상판 변위 시간이력에서 진폭이 최대가 되는 점을 선택한다. 그리고 변위 위상차는 입력파 변위와 상판 변위의 최대 진폭점의 시간 차이를 이용하여 식 (1)을 이용하여 계산할 수 있다.
| $$\psi_p=2\pi\frac{t_{dD}-t_{dB}}T$$ | (1) |
여기서, ψp=변위 위상차(radian), tdD = 상판변위 최대 진폭점 발생시간, tdB = 입력파 변위 최대진폭점 발생시간, T=파주기(= 0.667 sec)
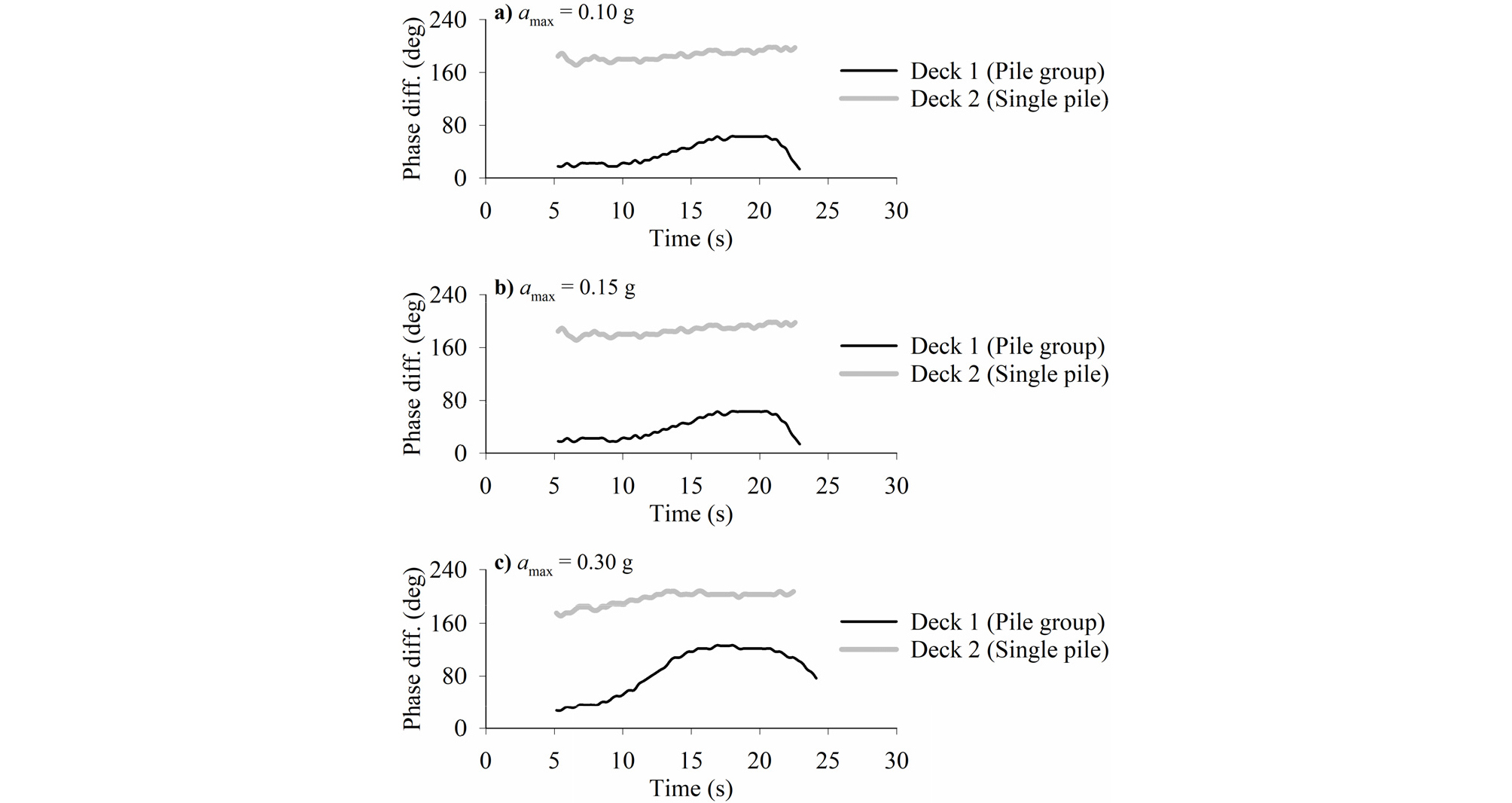
Fig. 8는 입력파 변위에 대한 상판 변위의 위상각 차이의 분석 결과이다. 위상각 차이의 (+)값은 입력파가 먼저 가해진 후 상판의 변위가 위상각 차이만큼 이 후에 발생하는 것을 의미한다. 입력가속도의 진폭이 약 15초까지 증가하면서 무리말뚝(Deck 1)의 위상차는 입력가속도 진폭에 비례하여 증가하는 경향을 보여주지만 단일말뚝(Deck 2)은 진폭에 관계없이 유사한 위상차를 보여준다. 입력가속도 진폭이 최대가 되었을 때 무리말뚝(Deck 1)과 단일말뚝(Deck 2)의 위상각 차이는 각각 평균적으로 80°와 180°였다. 무리말뚝의 경우 가속도 진폭이 작은 경우 무리말뚝의 수평강성이 크기 때문에 입력파와 위상차가 거의 동일하지만 가속도 진폭이 증가하면 주변 흙이 말뚝을 밀어주는 운동학적 힘이 증가하면서 위상차가 커지게 된다.
진동 중 지반의 변위와 입력파(토조)의 변위가 동일한 위상각을 가진다고 가정하면 단일말뚝 상판(Deck 2)과 말뚝 주변지반 변위의 위상차가 정반대(180°)이므로 단일말뚝이 진동 중 주변 흙에 의해 지지되는 효과가 발생하는데, 이러한 효과는 Yoo et al.(2017)의 실험에서도 유사한 결과가 얻어졌다. 반면에, 무리말뚝 상판(Deck 1)은 주변 지반이 말뚝을 밀어주는 효과가 발생하므로 주변지반이 말뚝에 추가적인 하중을 가하게 된다.
그러므로, Fig. 5의 단일말뚝과 무리말뚝의 휨모멘트 발생 차이는 다음과 같이 설명할 수 있다. 진폭이 0.10g일 때는 무리말뚝 두부의 회전구속 효과에 의해 무리말뚝의 최대 휨모멘트가 단일말뚝보다 약 0.5배로 작게 발생하였지만, 진폭이 0.15g와 0.30g일 때 지반변위가 증가하고 운동학적 힘이 말뚝에 추가적인 하중으로 작용하면서 무리말뚝의 최대 휨모멘트가 단일말뚝과 비교하여 각각 평균 1.74배, 3.3배로 증가하였다.
4. p-y 곡선의 산정
말뚝과 지반 사이의 동적 상호작용을 분석하기 위하여 말뚝 휨모멘트와 지반 가속도 계측자료 등을 이용하여 실험 p-y 곡선을 산정하였다. p는 말뚝과 지반 사이의 반력, y는 말뚝과 지반 사이의 상대변위로 정의된다.
실험 p-y 곡선을 산정하는 절차는 다음과 같다. 우선, 말뚝 변형률 측정값은 주파수 필터링 기법을 통해 여러 가지 전기적 신호에서 발생할 수 있는 측정 노이즈를 제거하였다. Low-pass 필터링 기법을 적용하여 고주파 노이즈를 제거하였으며 사면 변위에 의해 발생하는 잔류 변형률 성분은 제거하지 않았다(Nguyen et al., 2018). 필터링된 변형률 값은 보정계수를 곱하여 각 깊이에서의 휨모멘트 값 M(i)를 계산하였다. 그리고, 특정 시점에서 얻어진 이산화된 휨모멘트 값들을 이어주는 휨모멘트 곡선식 M을 산정한 후, 식 (1)과 식 (2)를 적용하여 휨모멘트 곡선식을 2번 미분 또는 2번 적분하면 횡방향 지반반력 p와 말뚝의 변위 yp값을 산정할 수 있다. 그리고, 말뚝과 지반 사이의 상대변위 y는 말뚝변위 yp에서 지반변위 ys를 빼서 산정한다.
| $$p=\frac{d^2M}{dz^2}$$ | (2) |
| $$y_p=\int\int\frac M{EI}dzdz$$ | (3) |
여기서, M = 휨모멘트 곡선식, EI = 말뚝의 휨강성, z = 지표면 아래의 깊이, yp= 말뚝변위
지금까지 많은 연구자들이 이산화된 말뚝의 휨모멘트 측정값을 부드럽게 연결해주는 휨모멘트 곡선식 함수를 제안한 바 있다. Brandenberg et al.(2010)과 Haiderali and Madabhushi(2016)는 여러 형태의 휨모멘트 곡선식을 비교한 결과 cubic spline 곡선식이 가장 좋은 결과를 준다고 제안하였다. 그러므로 본 연구에서는 cubic spline 곡선식을 적용하여 p-y 곡선을 산정하였다. p-y 곡선 산정을 위해 적용한 경계조건 및 가정사항은 다음과 같다.
① 지표면과 말뚝선단 위치의 지반반력 p=0으로 적용
② 말뚝 선단은 토조바닥면에 부착하여 회전을 고정시킴. 그러므로, 말뚝 선단의 변위와 회전각은 0으로 적용함. 이 경계조건은 휨모멘트 곡선식을 적분(1번 적분 말뚝회전각, 2번 적분 말뚝변위)할 때 적용함
③ 자유장 지반의 변위 ys는 지반 가속도계에서 측정된 가속도 시간이력을 2번 적용하여 산정함. 이 때, 가속도계 사이에 위치한 지반의 변위는 선형분포로 가정하여 선형보강법을 적용하여 계산함
④ 말뚝과 지반 사이의 상대변위 y는 말뚝 변위 yp에서 지반변위 ys를 빼서 산정함
⑤ 동적 p-y 곡선은 지반저항력 p와 말뚝-지반 상대변위 y의 관계로부터 산정함
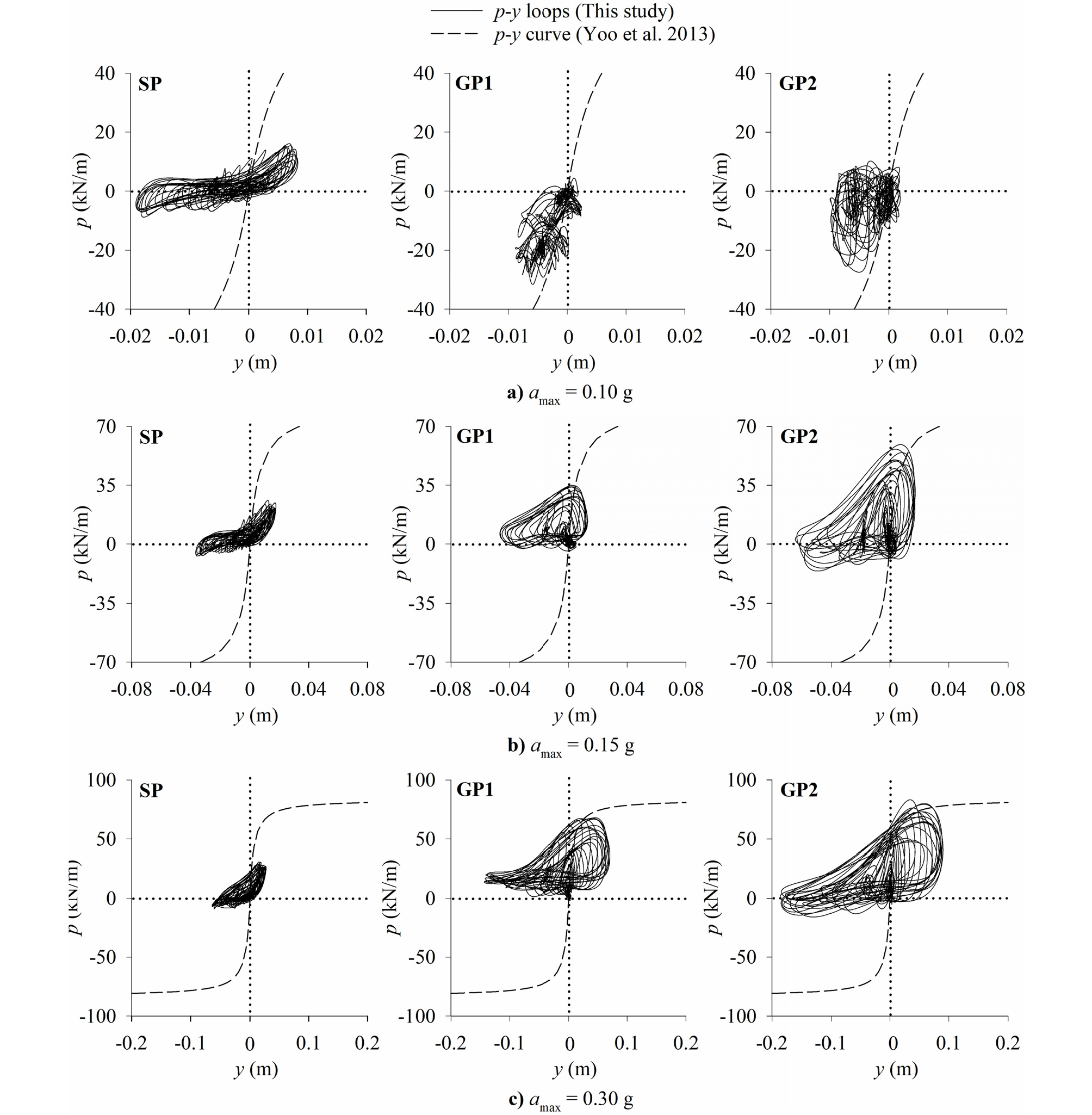
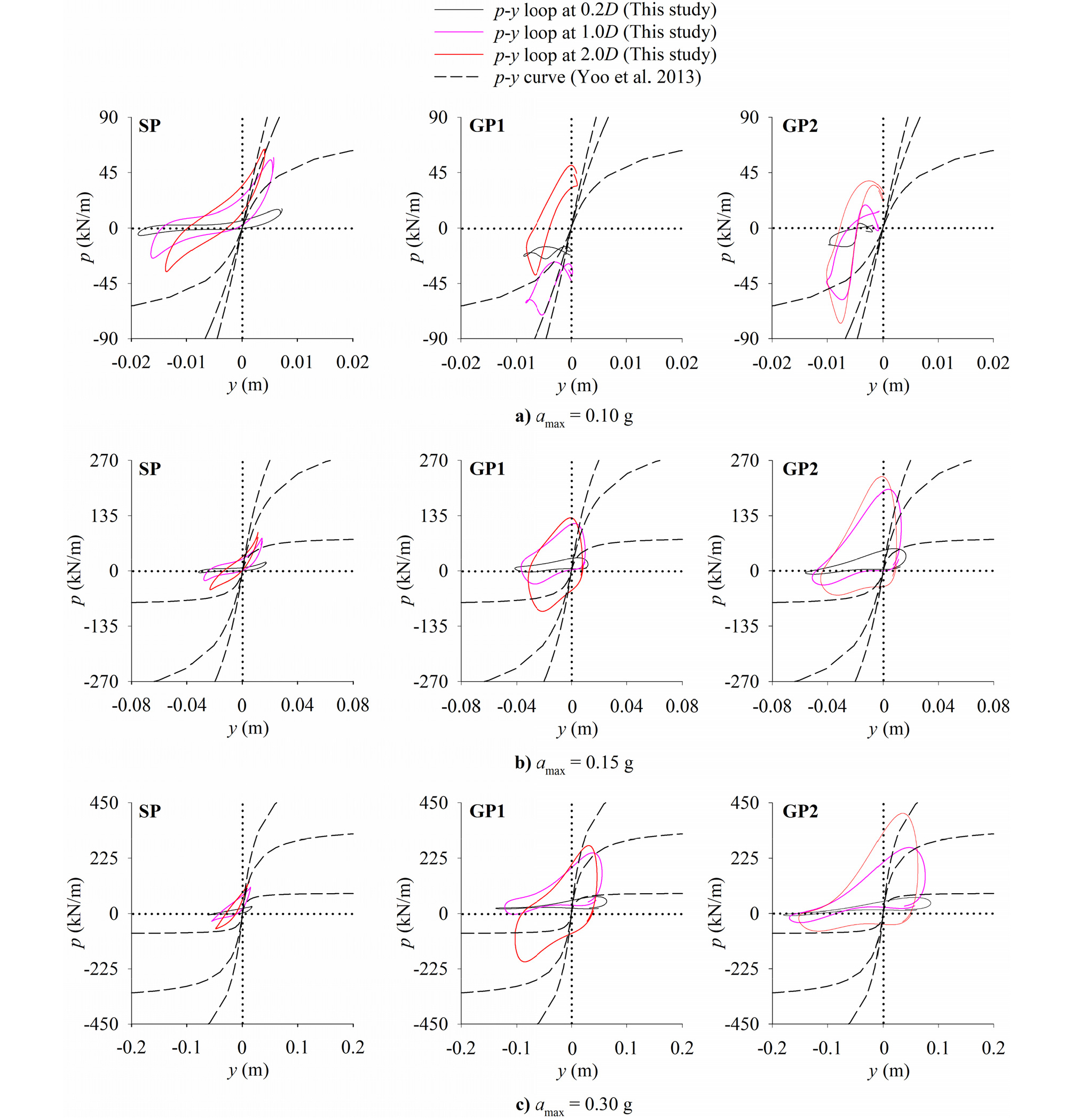
Fig. 9는 지반 깊이 0.2D(D=말뚝 직경)에서 얻어진 동적 p-y 곡선으로서 전체 진동시간에서의 값을 나타내었다. 진폭 0.10g일 때 단일말뚝의 경우는 1사분면(+y 값, +p 값)과 3사분면(-y 값, -p 값)에 정점이 위치하며 대칭 형상을 보여주었다. 그러나, 곡선이 점차 왼쪽(경사 하향 방향)으로 이동하는 경향이 나타났다. 그 이유는 y값을 산정할 때 yp값은 휨모멘트 측정자료로부터 산정하여 말뚝 잔류변위를 포함한 값이지만 ys값은 가속도 측정자료를 2번 적분하여 산정하므로 지반 잔류변위 영향을 반영하지 못하기 때문이다. 그러므로, Fig. 9의 y값은 말뚝 잔류변위의 영향이 포함되어 있으므로 잔류변위에 비례하여 곡선이 점차 왼쪽으로 이동하였다. 무리말뚝의 p-y 곡선은 휨모멘트 값이 단일말뚝의 평균 0.5배로 작게 발생하였기 때문에 곡선의 형상이 제대로 관찰되지 못하였다.
진폭 0.15g일 때 단일말뚝은 0.10g의 결과와 유사하게 1사분면(+y 값, +p 값)과 3사분면(-y 값, -p 값)에 정점이 위치하며 대칭 형상을 보여주지만, 무리말뚝의 p-y 곡선은 경사 하향으로 편향된 형태를 보여준다. 단일말뚝과 무리말뚝의 p-y 곡선 형상을 보면 말뚝이 지반 경사 상향으로 움직일 때(+y 값)의 지반 저항력(p)의 최대 크기는 하향으로 움직일 때(-y 값)와 비교하여 크게 증가하였으며 경사 상향의 변위(+y)값이 경사 하향 변위(-y)와 비교하여 크게 감소하였다. 이것은 지반 경사의 영향으로 말뚝이 경사 상향으로 움직일 때의 지반저항력이 경사 하향으로 움직일 때의 지반저항력과 비교하여 증가하였기 때문으로 판단된다. 또한, 진동 중 경사 하향의 지반 잔류변위가 발생하면서 말뚝을 하향으로 밀어주는 힘이 증가하면서 곡선의 p값이 상향으로 증가하였다. 이러한 영향으로, 경사 하향의 y 최대값은 무리말뚝의 경우 거의 2사분면(-y 값, +p 값)에 위치하였다. 그리고, p-y 곡선은 진동이 지속됨에 따라 말뚝의 잔류변위가 누적되기 때문에 왼쪽으로(-y방향)으로 이동하였다.
이와 같이 본 실험의 p-y 곡선은 지반 경사(진동방향에 따른 지반 저항력 차이), 지반의 잔류변위, 단일말뚝과 무리말뚝의 운동학적 힘(말뚝 모멘트 발생크기의 차이) 등 다양한 요인에 의해 매우 복잡한 형상을 보이게 된다.
Fig. 10은 깊이에 따른 동적 p-y 곡선으로 특정 시점에서의 대표적인 곡선만을 나타내었다. 곡선의 원점과 정점을 연결하는 경사는 지반 강성(soil stiffness) 값을 의미한다. 지반 강성 값은 깊이가 0.2D~2.0D로 깊어짐에 따라 구속압이 증가하면서 계속하여 증가하였다. 동적 p-y 곡선의 형상은 깊이가 깊어짐에 따라 점차 일반적인 p-y 곡선의 형상(1사분면과 3사분면에 정점이 위치하는 대칭 형상)과 유사해졌다.
Fig. 9와 Fig. 10에서 Yoo 등(2013)이 단일말뚝에 대하여 제안한 동적 p-y 곡선을 점선으로 표시하고 본 실험의 결과와 비교하였다. Yoo 등(2013)은 수평지반에 설치된 단일말뚝에 대한 원심모형실험을 수행하여 동적 p-y 곡선 산정식을 제안한 바 있다.
단일말뚝의 경우 Yoo 등의 곡선과 비교하여 말뚝이 경사 상향 또는 하향 방향으로 움직일 때 모두 지반 저항력이 작게 발생하였다. 그 이유는 말뚝이 경사 하향으로 움직이는 경우 지반의 저항력이 작기 때문으로 판단된다. 그리고, 말뚝이 경사 상향으로 움직이는 경우 본 연구에서 가속도를 2번 적분하여 산정한 흙의 변위 ys는 경사지반의 잔류변위 발생을 고려하지 못하는데 잔류변위에 의한 실제 ys증가를 고려하면 곡선의 경사가 증가할 수 있다.
무리말뚝의 경우에도 말뚝이 경사 하향으로 움직일 때 지반저항력은 Yoo 등의 곡선과 비교하여 작게 발생하였다. 그러나, 무리말뚝이 경사면 상향으로 움직일 때 무리말뚝의 지반 저항력이 Yoo 등의 곡선과 비교하여 크게 증가하였다. 그 이유는 운동학적 상호작용에 의한 단일말뚝과 무리말뚝의 변위 위상 차이 때문으로 판단되며, 이것은 지반의 강성, 기초시스템의 강성 그리고 입력가속도 진폭 등이 복합되어 발생하게 된다. 그리고, 단일말뚝과 마찬가지로 흙의 변위 ys 산정시 경사지반의 잔류변위 발생을 고려하지 못하였기 때문에 이를 고려하면 무리말뚝의 p-y 곡선의 경사가 증가할 수 있다.
5. 결 론
본 연구에서는 건조 사질토 경사 지반에 설치된 단일말뚝과 2×2 무리말뚝에 대한 원심모형실험을 수행하여 단일말뚝과 무리말뚝의 동적 거동과 지반-말뚝 상호작용을 분석하였다. 본 연구에서 얻어진 결론 및 요약은 다음과 같다.
(1) 무리말뚝의 최대 휨모멘트는 단일말뚝과 비교하여 진폭 0.10g, 0.15g, 0.30g에서 각각 평균 약 0.5배, 1.74배, 3.3배로 증가하였다. 입력가속도 진폭이 작은 경우(0.10g) 무리말뚝의 회전 구속에 의해 휨모멘트가 감소하였지만 입력가속도 진폭이 증가하면서(0.15g, 0.30g) 지반과 말뚝 사이의 운동학적 힘이 증가하면서 무리말뚝의 휨모멘트가 크게 발생하였다.
(2) 입력가속도 진폭이 최대가 되었을 때 무리말뚝과 단일말뚝 상판변위는 입력파 변위에 대하여 평균적으로 80°와 180°의 위상각 차이가 발생하였다. 단일말뚝의 변위는 말뚝 주변지반 변위와 정반대의 위상차를 가지므로 주변 흙의 운동학적 힘이 저항력으로 발휘되지만, 무리말뚝의 주변 지반은 말뚝에 추가적인 하중을 가하게 된다.
(3) 단일말뚝과 무리말뚝의 운동학적 힘의 차이에 의해 단일말뚝의 동적 p-y 곡선은 무리말뚝과 비교하여 곡선의 지반 강성과 최대 정점값이 작게 발생하였다. 그리고, 동적 p-y 곡선은 지반 경사(진동방향에 따른 지반 저항력 차이), 지반의 잔류변위, 단일말뚝과 무리말뚝의 운동학적 힘(말뚝 모멘트 발생크기의 차이) 등 다양한 요인에 의해 매우 복잡한 형상을 보이게 된다.