1. 서 론
2. 구성 모델
2.1 압밀 거동
2.2 변형률 분해 및 탄성 거동
2.3 한계상태
2.4 경계면
3. 수치해석
3.1 캘리브레이션
3.2 해설결과 및 토의
4. 요약 및 결론
1. 서 론
최근 신재생 에너지에 대한 관심과 더불어, 지중 열교환기 및 지중 축열기에 대한 관심이 증가하고 있다. 지중 열교환기를 여름철에 구동할 경우 온수가 지속적으로 지중을 통과하여 지반과 열교환을 하여, 지반에 잔열이 축척되어 지반의 온도가 지속적으로 올라갈 수 있다. 또한, 지중 축열기는 80도 이상의 고온수를 지반에 장기적으로 보관하여 겨울철에 난방에 활용하는 기술로, 축열기 인근 지반의 온도를 크게 상승시킬 수 있다. 하지만, 이러한 기술들에 대해서 현재까지 지반의 열전도도 및 열용량 등 열적 특성에만 초점을 맞추고 있으며, 온도의 변화에 따른 지반의 역학적 특성의 변화에는 면밀한 검토가 이루어지고 있지 않다.
극성을 띄는 미세 입자로 구성된 점성토의 압밀 및 전단거동을 포함한 역학적 거동은 온도에 큰 영향을 받는다(Abuel-Naga et al., 2007; Brochard et al., 2017; Graham et al., 2001; Hamidi et al., 2014; Neaupane et al., 2005; Plum and Esrig, 1969; Sultan et al., 2002). 온도에 따른 점성토의 역학적 거동에 대한 기존 연구(Abuel-Naga et al., 2007; Brochard et al., 2017; Graham et al., 2001; Neaupane et al., 2005; Plum and Esrig, 1969; Sultan et al., 2002)에 따르면, 점성토의 정규압밀선(Normal Consolidation Line, NCL)은 간극비 e와 평균유효응력 p'(= σ'kk/3, σ'ij은 유효응력(= σij – uδij), u은 간극수압)에 평면에서 온도가 증가할수록 아래쪽으로 이동을 한다. 이는 고정된 p' 아래에서 온도가 증가할 때, 점성토가 압축되거나 간극수가 배수된다는 것을 의미한다. 또한, 이는 동일한 간극비 e를 가지는 정규압밀 점성토의 경우, 온도가 높을수록 더 작은 선행압밀 유효응력 p'c을 가짐을 의미하며, 동일한 선행압밀 유효응력 p'c를 가지는 점성토의 간극비는 온도가 높아질수록 작아짐을 의미한다.
점토의 전단거동에 대하여 Hamidi et al.(2014)은 평균 유효응력 p'와 von Mises 응력 q(= ((3/2)sijsij)1/2, sij은 축차응력(= σ'ij – p'δij))의 공간에서 한계상태면(Critical State Surface, CSS)이 온도의 영향을 받을 수 있다고 제안한 반면, Abuel-Naga et al.(2007)와 Graham et al.(2001)은 온도가 한계상태면에 의미있는 영향을 주지 못한다고 발표하였다. 또한 Abuel-Naga et al.(2007)은 간극비 e와 평균 유효응력 p' 평면에서 한계상태선(Critical State Line, CSL)은 온도의 영향을 받지 않는다고 보고하였으나, Graham et al.(2001)은 온도가 증가함에 따라 정규압밀선 만큼은 아니지만 한계상태선이 e-p' 공간에서 아래쪽으로 약간 이동한다고 하였다. 상기 기존 연구를 종합해 볼 때, 점성토의 선행압밀 유효응력 p'c와 한계상태 유효응력 p'cs는 온도의 함수임을 알 수 있다.
이러한 점성토의 온도의 영향을 받는 역학적 거동을 수치적으로 모사하기 위하여 Modified Cam Clay(MCC) 모델을 기반으로 한 구성 모델(Graham et al., 2001; Hamidi et al., 2014; Wang et al., 2016)이 제안되어 왔다. 하지만, p'-q 평면 상에서 타원 형태를 갖는 항복면(혹은 경계면)을 가지는 MCC 모델의 특성상 한계상태 유효응력 p'cs과 선행압밀 유효응력 p'c의 비율은 0.5로 고정되어, 다양한 온도 하에서 전단거동을 현실감있게 모사하기 위하여는 복잡한 유동(Flow), 경화(Hardening), 발달(Evolution) 법칙 등이 필요하다.
본 연구는 이러한 복잡한 법칙 없이 간단하고 엄밀하게 점성토의 온도에 따른 역학적 거동을 모사할 수 있는 경계면을 제안한다. 또한, 제안된 경계면을 Bangkok 점성토에 대한 실험결과를 바탕으로 한 경계면 보정과정을 제시한다. 본 연구는 삼축조건을 기반으로 하여 경계면의 정식화를 제시하며, 이는 응력 불변량인 평균유효응력 p'와 von Mises 응력 q와 변형률 불변량인 부피 변형률 εvol(= εkk, εij은 변형률)과 전단변형률 εq(= ((2/3)eijeij)1/2, eij는 축차변형률(= εij – (1/3)εkkδij))을 기반으로 한다.
2. 구성 모델
2.1 압밀 거동
평균 유효응력 p'과 간극비 e의 공간에서 정규압밀선은 수학적으로 다음과 같이 표현된다.
여기서 enc는 정규압밀선 상에서의 간극비, pA는 기준압(= 100kPa), N은 p' = pA 일 때의 enc, 그리고 λ은 NCL의 e-lnp' 공간상에서의 기울기이다. 식 (1)을 간극비 e를 독립변수로 다시 쓰면 다음과 같다.
여기서 p'c는 선행압밀 유효응력이다. Abuel-Naga et al.(2007), Graham et al.(2001), Neaupane et al.(2005), Plum and Esrig(1969), Sultan et al.(2002)에 따르면, 온도가 상승함에 따라 정규압밀선은 e-lnp' 공간에서 동일한 기울기를 유지한 채 아래쪽으로 평행 이동한다. 이는 식 (2)에서 N 값이 온도의 함수로 표현됨을 의미한다. 본 연구에서는 이러한 온도 변화에 대한 거동 특성을 고려하기 위하여 다음과 같이 N을 온도의 선형 함수로 정의하였다.
여기서 T는 온도, Tref는 기준온도, Nref는 T = Tref일 때의 N, α는 온도의 따른 N의 변화를 반영하는 양의 재료상수이다. 식 (3)을 이용하여 본 연구에서는 온도가 상승할수록 N은 선형적으로 감소하며, 온도가 하강할수록 N은 선형적으로 증가하도록 설정하였다.
팽창 혹은 재압축 영역에서의 간극비 e와 평균유효응력 p'의 관계는 흔히 다음과 같은 팽창선(Swelling Line)으로 가정한다.
여기서, eoc는 팽창선에서의 간극비, enc,c는 정규압밀선에서 p' = p'c 일 때의 간극비, κ는 팽창선의 e-lnp' 공간에서의 기울기를 나타내는 상수이다.
2.2 변형률 분해 및 탄성 거동
본 연구에서는 부피 및 전단 변형률 증분은 다음 식과 같이 탄성 및 소성 변형률 증분의 합으로 가정하였다.
여기서 위첨자 e와 p는 각각 탄성 및 소성 변형률 증분을 나타낸다. Hooke의 법칙을 따를 때, 응력증분 불변량 dp', dq와 탄성 변형률 불변량 dεevol과 dεeq 사이의 관계는 다음과 같다.
여기서 K와 G는 각각 체적탄성계수(Bulk Modulus)와 전단탄성계수(Shear Modulus)이다. 점성토는 흔히 팽창 혹은 재압축 영역에서 탄성거동을 하는 것으로 가정하며, 이를 따라 본 연구에서는 체적탄성계수 K를 다음과 같이 κ의 함수로 가정하였다.
본 연구에서 점성토의 전단탄성계수 G는 체적탄성계수 K와 포아송 비 ν를 이용하여 다음과 같이 산정하였다.
2.3 한계상태
흙의 한계상태는 p'-q 평면과 같은 응력공간에서 정의되는 한계상태면(Critical State Surface)과 e-lnp' 공간에서 한계상태선(Critical State Line)으로 정량화할 수 있다(Woo et al., 2017; Woo and Salgado, 2015). 한계상태면은 p'-q 평면에서 흔히 다음과 같은 선형함수로 정의된다.
여기서, Mc는 한계상태면의 p'-q 평면에서의 기울기를 나타내는 한계상태 응력비이다. Hamidi et al.(2014)은 한계상태면이 온도의 영향을 소량 받는다고 보고한 반면, Graham et al.(2001)과 Abuel-Naga et al.(2007)은 한계상태면이 온도에 의해 의미 있는 영향은 받지 않는다고 하였다. 본 연구에서는 Graham et al.(2001)과 Abuel-Naga et al.(2007)를 따라 한계상태면은 온도의 영향을 받지 않는 것으로 가정하였다.
많은 선행 연구(Abuel-Naga et al., 2007; Chakraborty et al., 2013; Graham et al., 2001)에서 e-lnp' 평면에서 한계상태선은 정규압밀선과 평행하다고 가정하며, 이 때, 한계상태선은 다음 식과 같이 정의된다.
여기서 ecs는 한계상태선 상에서의 간극비, pA는 기준압(= 100kPa), Γ은 p' = pA 일 때의 ecs이다. 식 (10)을 간극비 e를 독립변수로 다시 쓰면 다음과 같다.
Abuel-Naga et al.(2007)은 한계상태선이 온도의 영향을 거의 받지 않는다고 하였으나, Graham et al.(2001)은 한계상태선도 정규압밀선과 마찬가지로 온도가 증가함에 따라서 아래쪽으로 이동한다고 보고하였다. 본 연구에서는 Graham et al.(2001)의 연구결과를 고려하여 정규압밀선의 경우와 유사하게 식 (10)의 Γ를 다음과 같은 온도의 선형함수로 설정하였다.
여기서 Γref는 T = Tref일 때의 Γ이며, β는 Γ의 온도에 따른 변화를 나타내는 양의 상수이다.
2.4 경계면
MCC 모델 파괴면은 응력 공간인 p'-q 평면에서 타원으로 표현되며, 이를 구성하기 위해서는 타원의 꼭지점과 오른쪽 끝단의 p'과 q가 필요하다. MCC 모델에서 경계면의 오른쪽 끝단은 선행압밀 평균유효응력 p'c에 대응하며, 따라서 그 좌표는 (p'c, 0)이다. MCC 모델 타원의 꼭지점의 좌표를 설정하기 위해서는 전단 파괴시 응력경로를 살펴볼 필요가 있다. MCC 모델에서 연합유동법칙(Associated Flow Rule)을 적용할 경우, 비배수 전단시 응력경로는 파괴면에 도달한 이후, 파괴면을 따라 이동하면서 최종적으로는 항복면의 꼭지점에 도달한다. 따라서 타원의 꼭지점은 한계상태시 응력상태를 나타내며 그 좌표는 (p'cs, Mcp'cs)가 된다. MCC 모델에서는 타원을 경계면으로 사용하므로 꼭지점의 p' 좌표는 경화(Hardening) 및 발달(Evolution) 법칙을 고려하지 않는다면 항상 타원 오른쪽 끝점의 절반(p'cs = 0.5p'c)이지만, 이 관계는 점성토에서 항상 성립하지는 않는다(Chakraborty et al., 2013). 따라서 MCC 모델을 이용하여, 점성토의 역학적 거동을 실제와 유사하게 모사하기 위하여 복잡한 유동, 경화, 전개 법칙 등을 필요로 한다.
본 연구에서는 Graham et al.(2001)을 따라, 한계상태선이 정규압밀선 만큼은 아니지만 온도가 증가함에 따라 아래로 이동함을 가정하였다. 따라서, p'cs/p'c 비는 온도변화에 따라 변화하며, 따라서 타원 형상을 갖는 MCC 모델의 파괴면을 이용하여 이를 모사하기 위해서는 훨씬 복잡한 흐름, 경화, 및 발달 법칙이 필요하다(Graham et al., 2001; Hamidi et al., 2014).
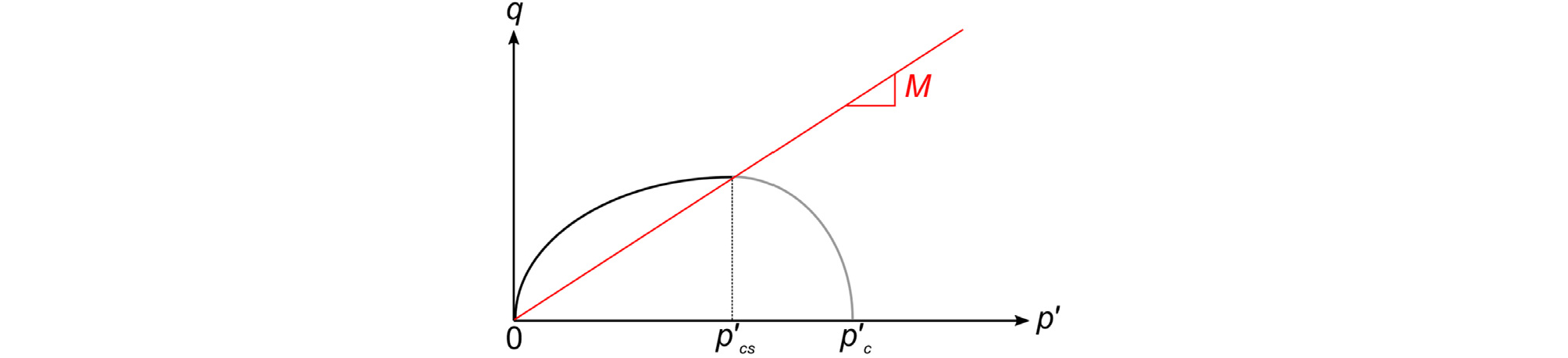
본 연구에서는 점성토의 열-역학적 거동을 간단하게 실제와 유사하게 모사하기 위하여, MCC 모델을 기반으로 왜곡 경계면을 새롭게 제안한다. Fig. 1은 본 연구에서 제안된 경계면을 p'-q 평면에 개념적으로 보여준다. Fig. 1에서 p' ≤ p'cs이면, 경계면의 왼쪽 끝단은 원점에 위치하고, 오른쪽 끝단의 좌표가 (2p'cs, 0)이며 꼭지점이 (p'cs, Mcp'cs)인 타원의 p' ≤ p'cs 영역에 해당한다. 만약 p' > p'cs 이면, 경계면은 왼쪽 끝단의 좌표가 (2p'cs – p'c, 0)이고, 오른쪽 끝단의 좌표가 (p'c, 0)이며, 꼭지점이 (p'cs, Mp'cs)인 타원의 p' > p'cs 영역에 해당한다. 이 경계면을 수학적으로 표현하면 다음과 같다.
3. 수치해석
3.1 캘리브레이션
본 연구에서는 제안된 경계면 모델을 이용하여 점성토의 열-역학적 거동을 모사하기 위해서는 Nref, λ, κ, ν, Γref, M, α, β을 실내실험을 통해서 산정해야 한다. 본 논문에서는 이를 위해 Abuel-Naga et al.(2007)이 Bangkok clay를 대상으로 수행한 실험적 연구 결과를 활용하였다.
Fig. 2는 Abuel-Naga et al.(2007)가 수행한 25°C와 70°C 온도에서 Bangkok clay의 등압 압밀 실험의 결과를 이용하여 e-p' 공간에서 정규압밀선 관련 계수인 Nref, λ, κ의 보정 과정을 보여준다. 본 연구에서는 기준 온도 Tref를 25°C로 설정하였으며, Fig. 2로 부터 Nref는 25°C에서의 N인 1.86로 설정하였다. Fig. 2에서 온도가 70°C으로 상승하면, 정규압밀선은 아래쪽으로 이동하여, N값은 1.76으로 감소한다. 이 값들을 식 (3)에 대입하면, 온도에 따른 정규압밀선의 이동 정도를 나타내는 α는 2.22e-3으로 산정된다. 정규압밀선의 기울기 λ와 팽창곡선의 기울기 κ는 Fig. 2에서 보이듯이 온도가 변화하더라도 크게 변하지 않음을 알 수 있다. 따라서, 본 연구에서는 Fig. 2로부터 λ, κ를 각각 0.405와 0.055로 설정하였다.
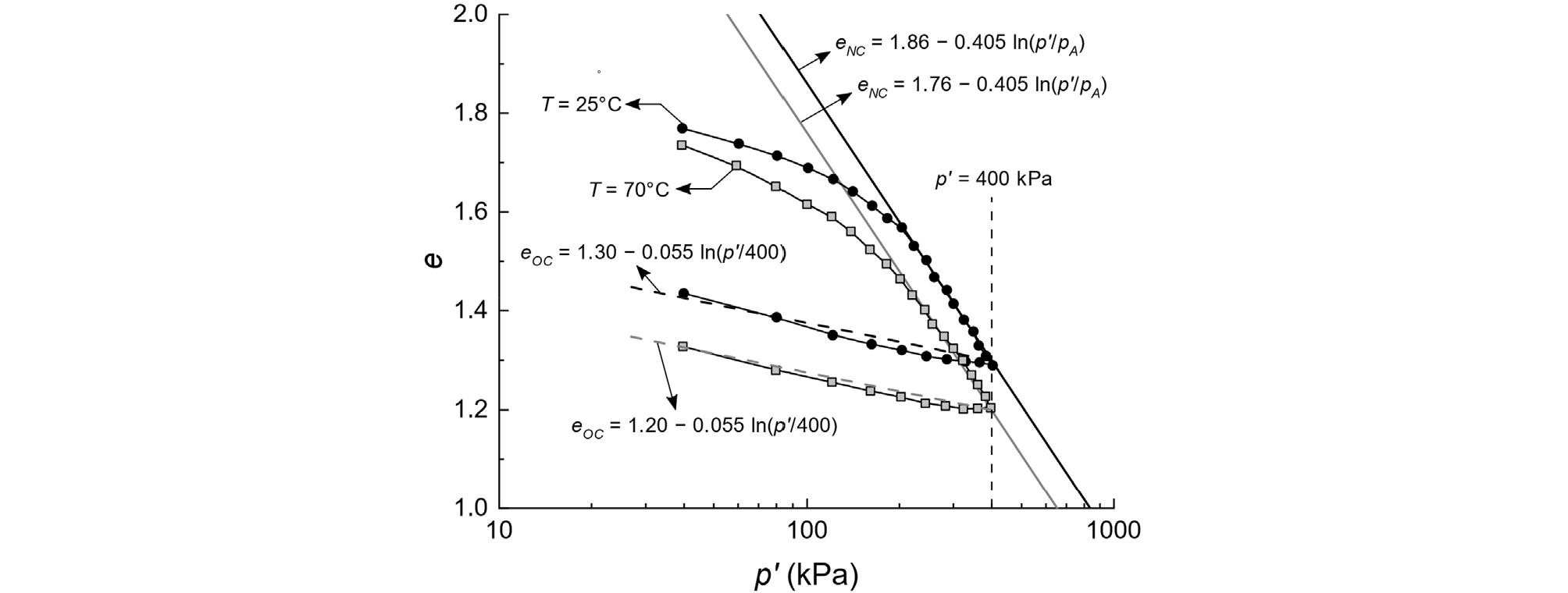
Fig. 2
Calibration of normal consolidation and swelling lines with respect temperature for soft Bangkok clay (experimental data from Abuel-Naga et al. (2007))
Fig. 3은 제안된 모델에서 p'-q 공간에서 한계상태면의 기울기인 M의 Bangkok 점토에 대해 보정한 결과를 보여준다. Fig. 3에서 심볼은 25°C와 70°C의 온도에서 수행한 비배수 삼축압축 시험(Abuel-Naga et al., 2007)에서 응력경로의 최종 목적지, 즉 한계상태 응력 상태를 나타낸다. Fig. 3에서 보이듯, 한계상태면의 기울기 M은 온도의 영향을 크게 받지 않으며, 본 연구에서는 Abuel-Naga et al.(2007)가 Bangkok 점토에 대하여 제안한 0.8로 M을 설정하였다. Fig. 4는 Bangkok 점토에 대해 한계상태선 계수인 Γref와 β의 보정 결과를 보여준다. Fig. 4에서 T = Tref = 25°C일 때, Γ는 1.66이므로, Γref = 1.66로 설정할 수 있다. 온도가 70°C 일 때, 한계상태선은 e-lnp' 공간에서 아래로 약간 이동하여 Γ는 1.62로 감소한다. 이러한 경향성을 바탕으로 본 연구에서는 식 (12)로부터 β는 8.89e-4로 결정하였다. 또한, Fig. 4는 e-lnp' 공간에서 한계상태선의 기울기가 정규압밀선의 기울기와 동일함을 보여준다. 본 연구에서 수행한 수치해석에서 점성토의 배수 포아송비 ν는 0.3으로 가정하였으며, Table 1은 Bangkok 점토에 대해서 Nref, λ, κ, ν, Γref, M, α, β을 산정한 결과를 보여준다.
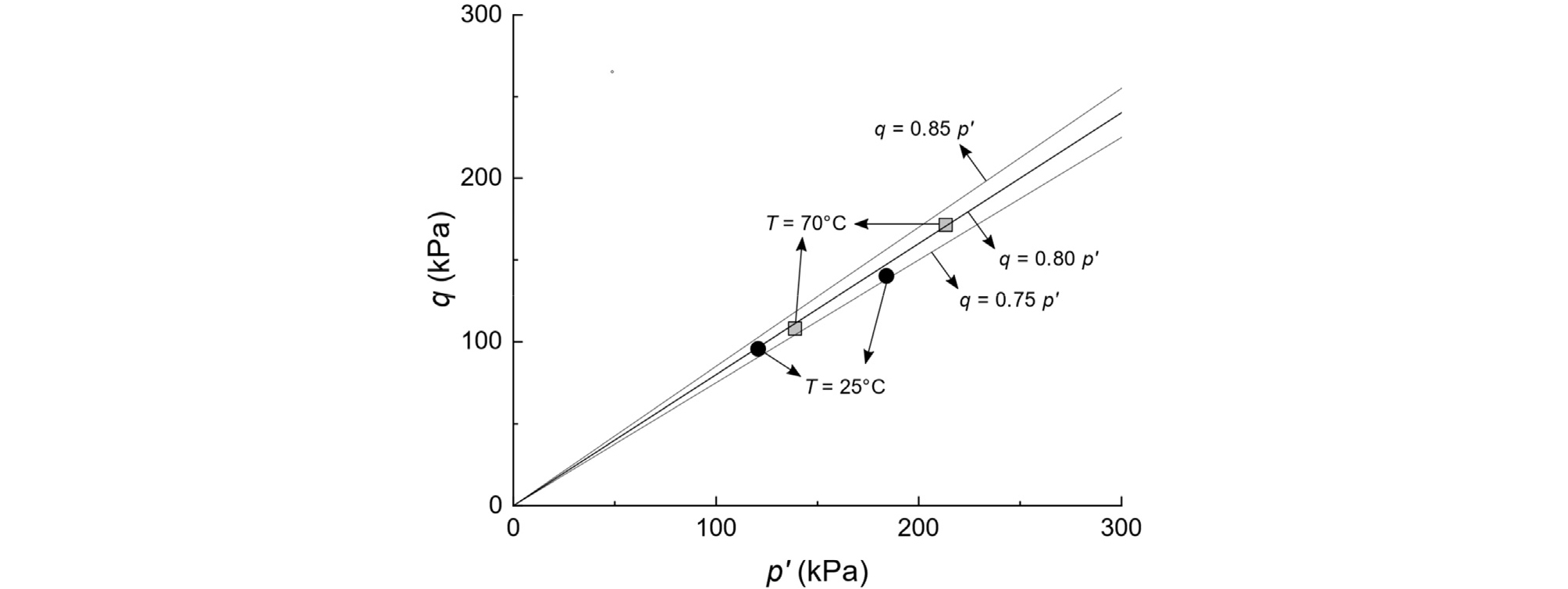
Fig. 3
Calbiration of critical state surface in the p'-q plane with respect to temperature for soft Bangkok clay (experimental data from Abuel-Naga et al. (2007))
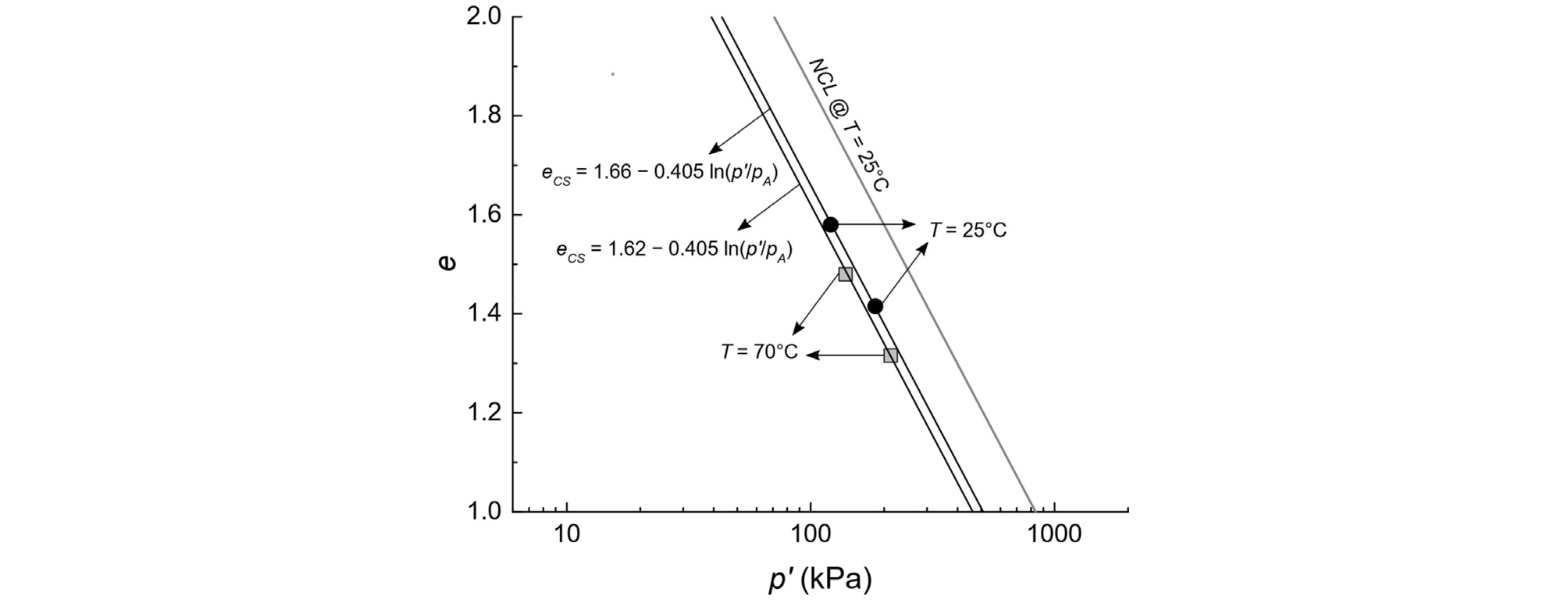
Fig. 4
Calbiration of critical state line in the e-lnp' plane with respect to temperature for soft Bangkok clay (experimental data from Abuel-Naga et al. (2007))
Table 1.
Model parameters of soft Bangkok clay used for the distorted bounding surface in this study
| Parameters | Value |
| Nref | 1.860 |
| Λ | 0.405 |
| Κ | 0.055 |
| ν | 0.300 |
| Γref | 1.660 |
| Mc | 0.800 |
| α | 2.22e-3 |
| β | 8.89e-4 |
3.2 해설결과 및 토의
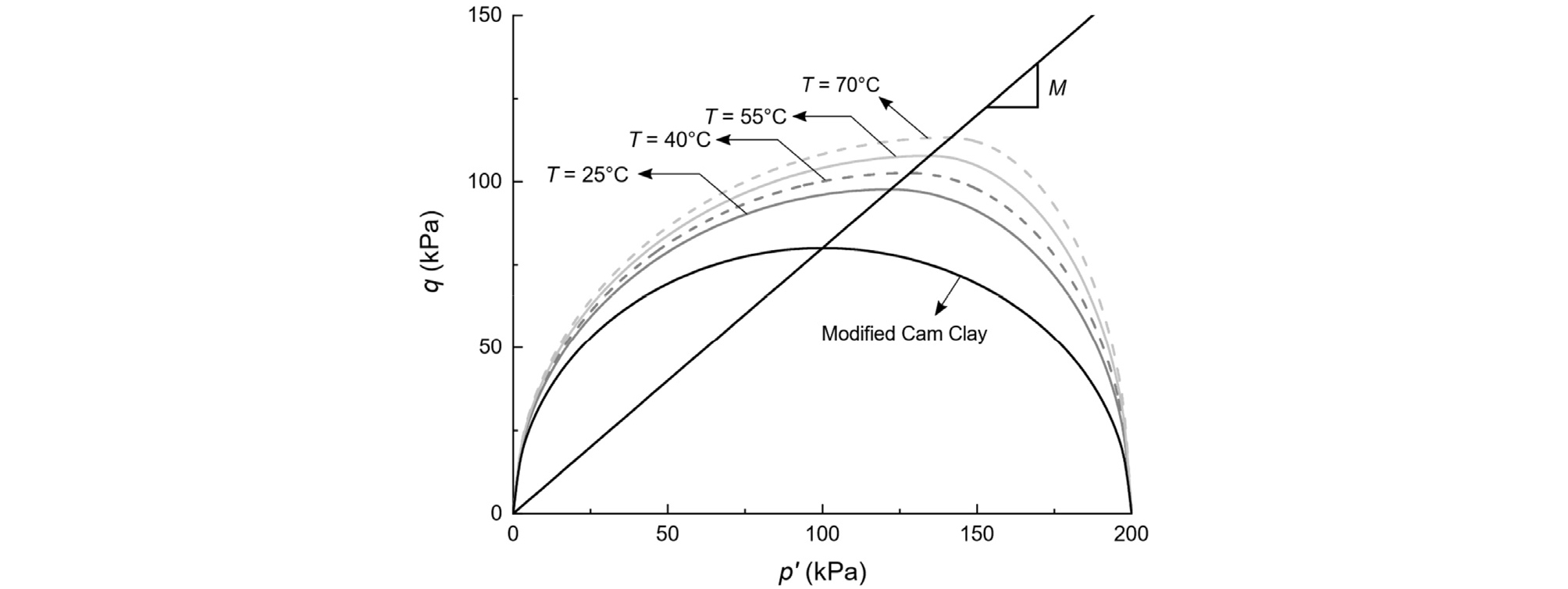
Fig. 5는 다른 온도에서 조성된 동일한 선행압밀 평균유효응력 p'c을 가지는 점성토의 경계면을 보여준다. Fig. 5에서 보이듯이 본 연구에서 제안한 경계면은 온도가 높아질수록 왜곡이 커진다. 온도가 높아질 때, e-lnp' 공간에서 식 (3)의 α가 식 (12)의 β보다 크므로(Table 1), 정규압밀선은 한계상태선 보다 더 많이 하향으로 이동한다. 따라서, p'c가 동일하다면, 정규압밀 점성토에서 온도가 높아질수록 p'cs는 p'c에 가까워진다. 반면에 온도는 한계상태면의 기울기 M에 영향을 거의 미치지 않으므로, 경계면의 꼭지점에서의 비율 qcs/p'cs(= M)은 일정하다.
본 연구에서는 Fig. 5와 같이 제안된 항복면을 검증하기 위하여, Abuel-Naga et al.(2007)에 의하여 수행된 등방압밀 비배수 삼축압축시험(CIUTXC) 결과에 대하여 다양한 요소 해석을 수행하였다. 비배수 삼축압축 시험에서는 배수를 허용하지 않아 압밀이 발생하지 않으므로, 본 요소해석에서 p'c와 M에 발달 법칙(Evolution Rule)은 적용하지 않았다. 즉, 해석과정에서 p'c와 M은 고정된다.
Fig. 6은 p'c = 200kPa에서 온도 T가 20°C와 70°C일 때, 정규압밀 Bangkok 점성토에 대한 CIUTXC 실험 데이터(심볼)와 수치해석결과(실선)를 보여준다. Fig. 6(a)은 실험 및 해석 결과를 축변형률 (Axial Strain)과 von Mises 응력(삼축조건에서는 축차응력) q의 공간에 도시하며, Fig. 6(b)는 이를 p'과 q의 공간에 도시한다. Fig. 7은 p'c = 300kPa에서 온도 T가 20°C와 70°C일 때, 정규압밀 Bangkok 점성토에 대한 CIUTXC 실험 데이터(심볼)와 수치해석결과(실선)를 보여준다. Fig. 7(a)은 실험 및 해석 결과를 축변형률과 q의 공간에 도시하며, Fig. 7(b)는 이를 p'과 q의 공간에 도시한다.
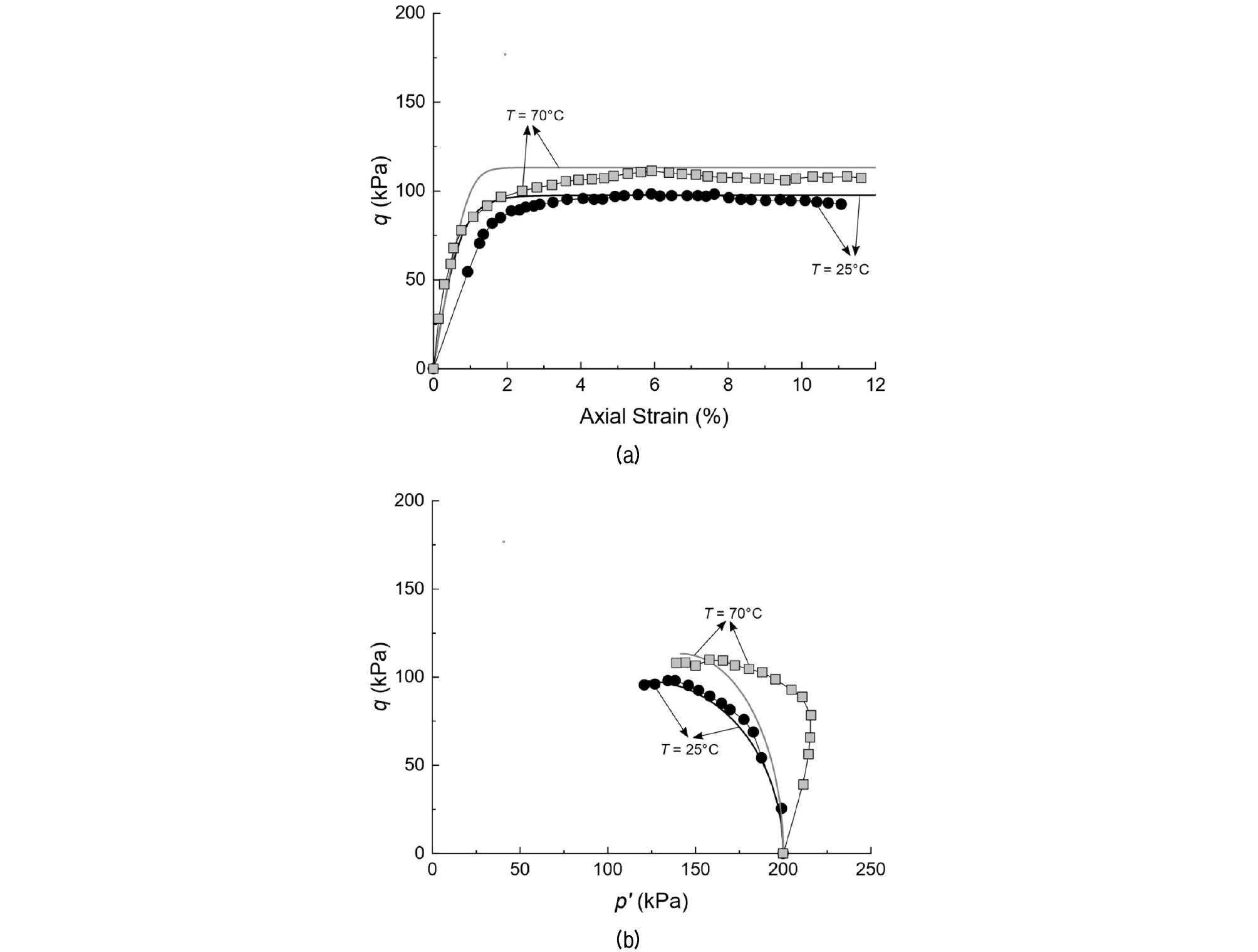
Fig. 6
Experimental data (symbols) and simulation results (lines) of CIUTXC for soft Bangkok clay with initial p' = 200 kPa (experimental data from Abuel-Naga et al. (2007)): (a) Axial strain vs. von Mises stress q, (b) mean effective stress p' vs. q
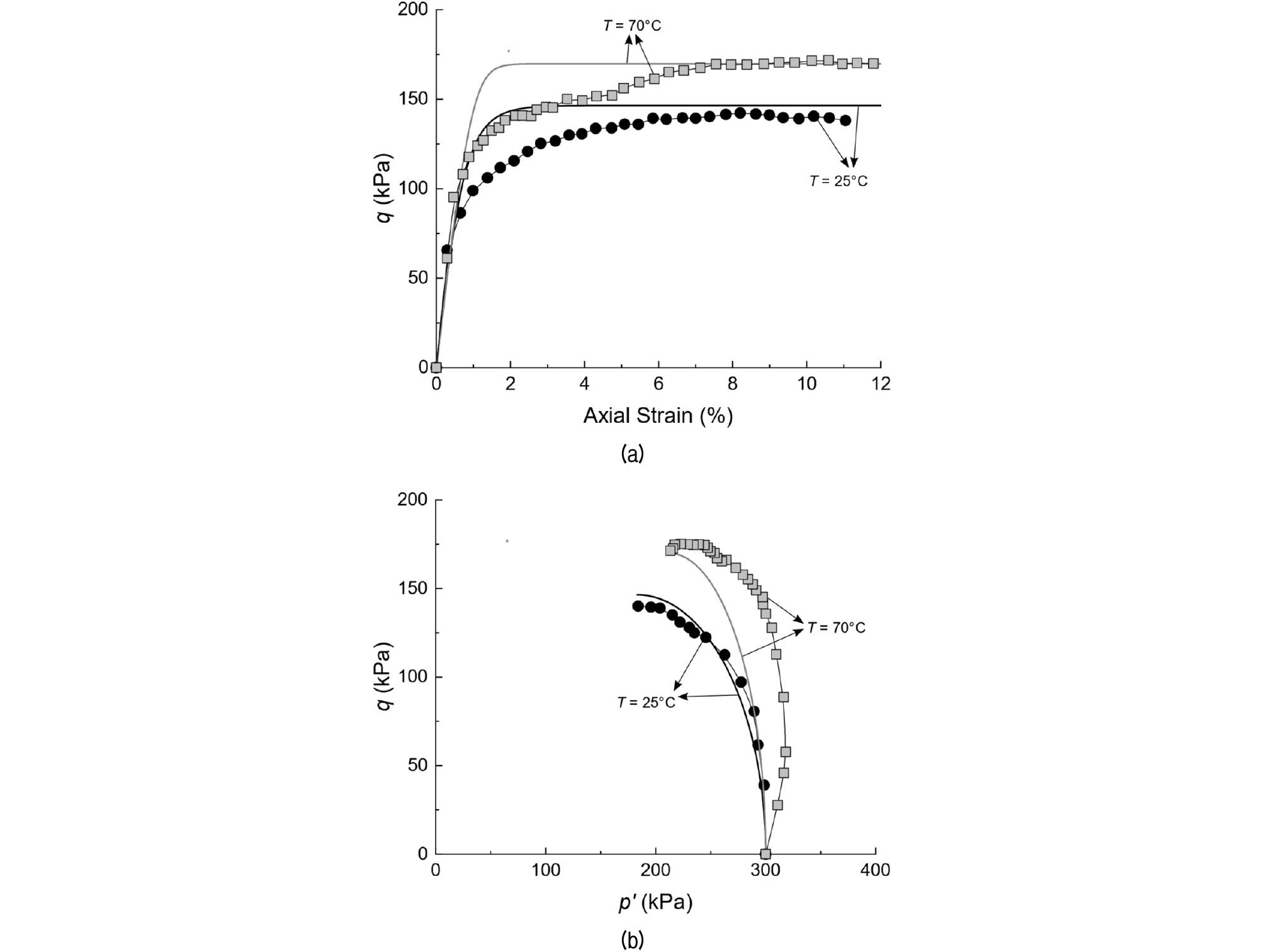
Fig. 7
Experimental data (symbols) and simulation results (lines) of CIUTXC for soft Bangkok clay with initial p' = 300 kPa (experimental data from Abuel-Naga et al. (2007)): (a) Axial strain vs. von Mises stress q, (b) mean effective stress p' vs. q
Fig. 6과 Fig. 7에서 제안된 경계면을 활용하여 제안된 응력-변형률 반응과 실험 결과를 비교해 보면, 초기 거동에 약간의 불일치가 있지만, 축변형률 4% 이후에는 실험결과와 해석결과가 유사함을 알 수 있다. 초기 거동의 차이는 탄성계수(G 와 K)와 밀접한 연관이 있기 때문에, 실험 결과를 더욱 유사하게 모사하기 위해서는 G와 K에 대하여 개선된 정식화가 필요하다.
Fig. 6(b)과 Fig. 7(b)에서는 제안된 모델이 p'-q 평면에서의 응력경로를 T = 25°C일 때 어떠한 전개법칙 없이도 실험결과를 매우 잘 모사하고 있는 것을 보여준다. 하지만, Fig. 6(b)과 Fig. 7(b)은 T = 70°C 일 때는 전단 초기에는 실험데이터와 해석결과의 차이가 존재한다. 일반적으로 정규압밀 점성토에 대해 등방압밀 비배수 삼축압축 실험을 수행하면, 압축성 Dilatancy 현상이 발현되어, 전단초기부터 양의 과잉간극수압이 발현되어 p'이 지속적으로 감소하여 한계상태에 진입한다. Fig. 6(b)과 Fig. 7(b)에서 온도가 25°C로 실온과 유사할 때의 실험결과는 이러한 경향성과 부합함을 알 수 있다. 하지만, 온도가 70°C로 높을 때는 전단 초기에 과잉간극수압이 거의 발현되지 않고, 배수 거동과 유사한 응력경로가 형성되다, 그 후, 양의 간극수압이 발현되어 한계상태에 진입함을 알 수 있다. 이 같은 현상은 온도에 따른 정규압밀선의 위치와 Dilatancy 현상으로 설명이 가능하다. Fig. 2에서 보이듯, 정규압밀선은 온도의 상승에 따라 하향 이동하며, 따라서 동일한 p'c를 가지는 점성토는 온도가 높을수록 더 작은 간극비 e를 가지며(온도가 높을수록 점성토가 더욱 조밀하며), 전단시 압축성 Dilatancy의 경향성을 감쇄되게 된다. 상기와 같은 이유로 Abuel-Naga et al.(2007)의 실험에서 온도가 70°C일 때, 정규압밀 점성토라도 전단초기에 압축성 Dilatancy가 억제되어 양의 과잉간극수압의 발현이 억제되고, 이에 따라 비배수 응력경로는 배수 응력경로와 유사하게 산정된다. 이 같은 경향성을 수치적으로 실험값과 유사하게 모사하기 위해서는, 점성토의 현재 간극비가 Dilatancy 거동에 미치는 영향, 비배수 전단시, p'가 기존 선행압밀 평균유효응력 p'c를 넘어섬에 따른 p'c의 발달 등의 고려가 필요하나, 이는 본 연구의 연구범위를 벗어난다. 반면, Fig. 6(b)과 Fig. 7(b)에서 제안된 모델은 한계상태에 해당하는 응력경로의 최종 도달 지점은 정확하게 모사함을 보여준다. 비배수 전단시험에서 한계상태에 해당하는 von Mises 응력 q은 점성토의 비배수 전단강도 cu에 대응하며, 이는 점성토 지반의 설계시 가장 중요하게 사용된다. 따라서 온도에 따른 점성토 지반의 전단시 최종지점인 한계상태를 파악하는 것은 매우 중요하다.
4. 요약 및 결론
본 연구에서는 Modified Cam Clay 모델을 기반으로 하여, 두개의 타원으로 구성된 왜곡 경계면 모델을 활용하여, 점성토의 전단과정에서 온도의 영향을 고려할 수 있는 방법론을 제안하였다. 온도가 상승할수록 점성토의 정규압밀선(Normal Consolidation Line)은 e-lnp' 평면에서 기울기를 유지한체 하향 이동한다. 점성토의 한계상태선(Critical State Line)은 e-lnp' 평면에서 흔히 정규압밀선과 평행하며, 온도가 상승할수록 정규압밀선과 마찬가지로 하향 이동하나, 그 이동량은 정규압밀선에 비해 작다. 따라서 온도가 상승할수록, 점성토의 한계상태 유효응력 p'cs의 선행압밀 유효응력 p'c에 대한 비율 p'cs/p'c는 증가한다. 전통적인 Modified Cam Clay 모델의 파괴면은 p'-q 공간에서 타원의 형상을 가지며, 따라서 p'cs/p'c의 비율은 0.5로 고정되어 있다. 이러한 한계점을 극복하고, 온도에 따른 점성토의 전단거동을 간단히 표현하기 위해, 본 연구에서는 p'cs를 기준으로 둘로 나뉘어진 파괴면을 경계면으로 적용하였다.
본 연구에서는 Bangkok 점성토에 대해서 정규압밀선, 한계상태선, 한계상태면을 구축하고, 온도에 따른 정규압밀선과 한계상태선을 변화를 또한 고려하였다. 또한, Bangkok 점성토에 대해서 경계면을 구축하고, p'c가 같은 점성토의 경계면의 형태는 온도가 상승함에 따라 점점 왜곡되는 것을 확인하였다. 그 후, 보정된 경계면을 활용하여 Bangkok 점성토에 대해 비배수 삼축압축시험에 대해 요소해석을 실시하였다. 요소해석 결과, 제안된 모델은 복잡한 강성 혹은 발달 법칙 없이 실험 데이터와 유사한 점성토의 온도에 따른 역학적 거동을 잘 모사함을 알 수 있었다.