1. 서 론
2. 구성모델
2.1 탄성 거동
2.2 탄소성 거동
3. 콘관입시험의 유한요소를 이용한 수치적 모사
3.1 모형 지반
3.2 콘관입체와 모래사이의 마찰
3.3 형상 및 격자의 구성
4. 해석 결과
5. 요약 및 결론
1. 서 론
사질토 지반에서 콘관입시험은 사질토의 전단강도 산정(Jamiolkowski et al., 2003), 상대밀도 산정(Jamiolkowski et al., 2003), 액상화 잠재성 판단(Stark and Olson, 1995) 등에 활용되고 있다. 콘관입시험은 깊은 관입의 일종으로 강성이 큰 관입체가 강성이 작은 지반을 관입하는 과정이다. 깊은 관입의 수치해석을 수행할 때에는 지반 내 발생하는 대규모 변위 및 관입체와 지반사이에 마찰저항을 반드시 고려해야 한다.
현재까지 유한요소법을 기반으로 깊은 관입시 발생하는 지반의 대변형을 모사하기 위해 Adaptive Meshing(Kardani et al., 2012; Nazem et al., 2006, 2012; Susila and Hryciw, 2003; Yu et al., 2008)과 Arbitrary Lagrangian Eulerian(Nazem et al., 2008; Sabetamal et al., 2014; Sheng et al., 2009; Vavourakis et al., 2013) 방법 등이 제안되어 왔다. 하지만 이러한 방법들은 복잡한 정식화 과정이 필요하며, 유한요소 해석 시 상당한 추가 연산을 요구하고, 또한, 격자의 재설정시 응력, 변형률, 간극비와 같은 상태 변수들의 내삽(혹은 외삽)을 요구한다. Hügel et al.(2008)은 경사진 관입체에 대해서 Lagrangian 유한요소법을 적용할 수 있도록 관입 유도체 개념을 제안하였다. Hügel et al.(2008)에 따르면, 관입 유도체를 사용할 경우, 해석 중간에 격자를 재조정할 필요가 없으며, (콘관입시험과 같이) 관입체와 지반 사이의 마찰 저항이 작을 경우에는, 관입체 주위 요소가 해석결과에 영향을 줄 정도로 크게 왜곡되지 않는 것으로 나타났다. 본 연구에서는 Hügel et al.(2008)을 따라 관입 유도체를 활용하여 콘관입시험을 유한요소법을 이용하여 모사하였다.
사질토의 역학적 거동을 모사하기 위해서 현재까지 많은 연구에서 Mohr Coulomb(MC) 소성모델을 활용하고 있다(Abbo and Sloan, 1996; Coetzee et al., 2005; Dang and Meguid, 2010; Huang et al., 2004; Kardani et al., 2012; Lam et al., 2009; Loukidis et al., 2008; Mohammadi and Taiebat, 2015; Nazem et al., 2012, 2006, 2008; Sabetamal et al., 2014; Sheng et al., 2009; Sheng and Sloan, 2001; Sloan et al., 2001; Sołowski and Sloan, 2015; Vavourakis et al., 2013; Yu et al., 2008). 모래와 같은 입상 재료의 전단변형은 부피변화를 유발하며, 이를 Dilatancy 현상이라 한다. 일반적으로 MC 소성 모델에서는 Dilatancy 현상을 모사하기 위해서 팽창각(Dilatancy Angle)을 이용하여 항복함수와는 다른 소성잠재함수를 정의한다. 이때, 대부분 연구에서 팽창각을 상수로 가정하여 MC 모델을 사용하고 있다. 하지만, Bolton(1986)은 계속되는 전단 시 모래는 한계상태에 진입하게 되고, 한계상태에서 팽창각은 소멸되며 마찰각은 한계상태 마찰각과 동일하게 된다고 언급하였다. 이로부터 팽창각과 마찰각은 상수가 아닌 한계상태와 현재상태 위상차의 함수임을 알 수 있다. 이러한 배경을 바탕으로 Woo et al.(2017)은 한계상태 이론을 기반으로 기존의 MC 모델을 수정하여 한계상태 MC 모델을 제안하였으며, 본 논문은 한계상태 MC 모델을 기반으로 사질토 지반의 콘관입시험을 수치적으로 모사하였다.
본 논문의 목적은 모래의 실제 거동을 잘 표현할 수 있는 한계상태 MC 모델을 활용하여, 상대적으로 간단하고 접근성이 뛰어난 Lagrangian 유한요소법을 이용하여 콘관입시험을 모사함에 있다. 본 논문의 구성은 다음과 같다. 2장에서는 구성모델인 한계상태 MC 모델에 대해서 간단히 언급한다. 3장의 주요내용은 콘관입시험 유한요소 해석을 위한 설정이며, 4장에서는 수치해석 결과를 분석하고 실험결과와 비교한다. 본 논문의 요약과 결론은 5장에서 언급된다.
2. 구성모델
2.1 탄성 거동
본 연구에서는 사질토의 탄성 거동을 모사하기 위해서 전단 탄성 계수 G와 포아송비 ν를 사용하였다. 포아송비는 이전 문헌 연구(Li et al., 1999; Loukidis and Salgado, 2009; Manzari and Dafalias, 1997; Woo et al., 2017; Woo and Salgado, 2015)를 바탕으로 상수로 가정하였으며, 전단 탄성 계수는 간극비와 응력의 함수로 가정하였다. Richart et al.(1970)은 사질토의 최대 전단 탄성 계수 G0를 다음 식과 같이 간극비 e와 평균 유효 응력 p'(= (1/3)tr(σ'))의 함수로 제안하였다.
| $$G_0=C_g\frac{(2.97-e)^2}{1+e}p'p_a$$ | (1) |
여기서 Cg는 양의 상수이며, pa는 대기압(= 100kPa)이다. 일반적으로 전단 탄성 계수 G는 전단 변형률이 증가함에 따라 최대값 G0에서 감쇠한다(Kramer, 1996). Papadimitriou and Bouckovalas(2002)와 Loukidis and Salgado(2009)는 전단 탄성 계수의 감쇠를 감쇠함수 T를 사용하여 다음과 같이 표현하였다.
| $$G=\frac{G_0}T$$ | (2) |
여기서, 감쇠 함수 T는 아래 식으로 정의된다.
| $$T=1+2\left(\frac1\alpha-1\right)\min\left[\frac{\sqrt{1/2(\mathbf r-{\mathbf r}_{ini}):(\mathbf r-{\mathbf r}_{ini})}}{2\alpha(G_{0,ini}/p'_{0,ini})\gamma_{tv}},\;1.0\right]$$ | (3) |
여기서, α는 상수, G0,ini은 초기 G0, p'ini는 초기 p', γtv는 체적 변화 경계 변형률(Volumetric Threshold Strain, Vucetic, 1994), r은 정규화된 편차응력 (= s/p', 편차응력 s = σ' – (1/3)tr(σ')I), rini은 초기 r이다. 체적 탄성 계수(Bulk Modulus) K는 전단탄성계수 G와 포아송비 ν를 이용하여 탄성론에 의해 다음 식과 같이 계산한다.
| $$K=\frac{2G(1+\nu)}{3(1-2\nu)}$$ | (4) |
2.2 탄소성 거동
현재까지 Mohr Coulomb(MC) 소성 모델은 사질토의 역학적 거동을 나타내기 위해 수많은 수치해석 관련 연구에서 사용되어 왔다(Abbo and Sloan, 1996; Coetzee et al., 2005; Dang and Meguid, 2010; Huang et al., 2004; Kardani et al., 2012; Lam et al., 2009; Loukidis et al., 2008; Mohammadi and Taiebat, 2015; Nazem et al., 2012, 2006, 2008; Sabetamal et al., 2014; Sheng et al., 2009; Sheng and Sloan, 2001; Sloan et al., 2001; Sołowski and Sloan, 2015; Vavourakis et al., 2013; Yu et al., 2008). MC 소성 모델의 항복 평면은 MC 파괴 모델의 파괴 평면과 동일하다. 처음에 제안된 MC 항복 평면의 경우, 모서리 부분에 불연속점이 존재하며, 이는 미분 불가능한 지점으로 소성 변형률을 명시적으로 구할 수가 없다. 이를 보완하고자, Sloan and Booker(1986)은 식 (5)와 같이 모서리가 둥근 MC 항복 평면을 제안하였다.
| $$f=\sqrt{J_2}K-p'\;\sin\phi=0$$ | (5) |
여기서, 은 마찰각, K는 MC 항복 평면의 모서리를 둥글게 만들기 위한 함수, J2(= (1/2s:s)1/2)은 편차응력(s = σ' – (1/3)tr(σ'))의 불변값이다.
MC 소성모델에서 Associated Flow Rule을 적용할 경우, 팽창각과 마찰각이 동일하게 되며, 전단 변형시 모래의 Dilatancy 현상을 과대평가하는 것으로 알려져 있다(Lubliner, 1990). 이러한 과대평가를 막기위해, MC 소성모델에서 일반적으로 Non-associated Flow Rule을 적용하며, 항복 함수와 동일한 형태이나 마찰각()을 팽창각()으로 교체한 소성잠재함수(Plastic Potential Function)를 사용한다.
| $$g=\sqrt{J_2}K-p'\;\sin\phi_d=0$$ | (6) |
많은 기존 연구에서는 사질토의 역학적 거동을 평가하기 위해서, 팽창각을 상수로 가정하여 수치해석을 수행하여 왔다(Huang et al., 2004; Lam et al., 2009; Loukidis et al., 2008; Susila and Hryciw, 2003). 하지만, 팽창각을 상수로 설정할 경우, 전단변형시 조밀한 모래는 팽창하며 느슨한 모래는 수축하는 밀도에 따른 Dilatancy 현상의 변화를 고려할 수 없다. 또한, Bolton(1986)에 따르면, 사질토에 계속된 전단변형이 발생하여 한계상태에 도달할 경우, 구속압-밀도간의 평형이 유지되어 더 이상 부피변화가 발생하지 않지만, 만약 팽창각을 상수로 가정할 경우, 사질토는 한계상태 도달 여부에 상관없이 계속적으로 팽창하게 된다. 이러한 문제점을 보완하고자, Woo et al.(2017)는 한계상태 토질역학을 기반으로 하여 수정된 Mohr Coulomb 소성모델을 제안하였다.
한계상태 이론에 따르면, 사질토의 계속된 전단변형시, 최종적으로 도달하는 e-p' 상태를 나타내는 한계상태선(Critical State Line)이 존재한다. Li and Wang(1998)에 따르면, 사질토의 한계상태선은 다음 식과 같이 표현된다.
| $$e_{cs}=\Gamma_{cs}-\lambda\left(\frac{p'}{p_a}\right)^\xi$$ | (7) |
여기서 ecs는 한계상태 간극비, p'는 현재 평균유효응력, pa는 대기압(= 100kPa), Γcs은 p' = 0일 때의 한계상태 간극비, 그리고 λ와 ξ은 양의 상수이다. Been and Jefferies(1985)는 e-p' 평면 상에서의 현재상태를 한계상태를 기준으로 정량화하기 위해 상태 매개 변수 ψ를 식 (8)과 같이 제안하였다.
| $$\psi=e-e_{cs}$$ | (8) |
식 (8)에 따르면, e-p' 상태가 한계상태선 아래에 있을 경우에는(사질토가 조밀할 경우에는), 상태 매개 변수 ψ가 음수가 되며, e-p' 상태가 한계상태선 위에 있을 경우에는(사질토가 느슨할 경우에는) ψ는 양수가 된다. 사질토가 한계상태에 도달한다면, ψ = 0이 된다. 이러한 점을 착안하여 Woo et al.(2017)은 팽창각 를 식 (9)와 같이 상태 매개 변수 ψ의 선형함수로 제안하였다.
| $$\phi_d=-d_0\psi$$ | (9) |
여기서, d0은 상수이다. 식 (9)에 따르면, 조밀한 사질토(e < ecs)는 전단시 팽창하고(ψ < 0, > 0), 간극비는 증가한다. 반면, 느슨한 사질토(e > ecs)는 전단시 수축하고(ψ > 0, < 0) 간극비는 감소한다. 따라서, 전단시 모래의 e-p' 상태는(느슨하든 조밀하든) 점점 한계상태선으로 이동하게 되며, 이에 따라 ψ의 절대값을 감소하며, 팽창각 의 절대값 또한 감소한다. 모래가 한계상태에 도달한 경우에는(ψ = 0), 팽창각 은 소멸되어 더 이상 Dilatancy 현상이 발생하지 않는다.
Bolton(1986)에 따르면, 총 마찰각 은 한계상태 성분과 팽창 성분으로 나눠지며, 수학적으로 식 (9)와 같이 표현될 수 있다.
| $$\phi=\phi_{cs}+0.8\phi_d$$ | (10) |
식 (10)에 팽창각에 관한 식 (9)를 대입하면 한계상태 MC 모델에서 사용하는 마찰각은 식 (11)과 같이 표현된다.
| $$\phi=\phi_{cs}-0.8d_0\psi$$ | (11) |
따라서, 현재 상태가 조밀할 경우(ψ < 0), 마찰각은 한계상태 마찰각보다 크다. 전단이 진행될 경우, 현재 상태는 한계상태로 이동하며(ψ → 0), 이 경우, 마찰각은 지속적으로 감소하여 한계상태에서는(ψ = 0) 한계상태 마찰각과 같게 된다. 따라서 첨두값을 지난 후 한계상태로 연화 거동을 보이는 조밀한 모래의 응력-변형률 관계를 모사할 수 있다. 현재상태가 느슨할 경우(ψ > 0), 마찰각은 한계상태 마찰각보다 작다. 계속되는 전단에 현재 상태는 한계상태로 이동하며(ψ → 0), 이 경우, 마찰각은 지속적으로 증가하여, 한계상태에 돌입하면(ψ = 0), 한계상태 마찰각과 동일하게 된다. 따라서 첨두값 없이 바로 한계상태로 진입하는 느슨한 모래의 역학적 거동을 모사할 수 있다.
3. 콘관입시험의 유한요소를 이용한 수치적 모사
3.1 모형 지반
본 연구에서는 Salgado(1993)에 의해 캘리브레이션 챔버에 조성된 Toyoura 모래 지반에 대해 수행된 콘관입시험을 수치적으로 모사하였다. 캘리브레이션 챔버의 반경은 600mm이고, 모형지반은 대략 1400mm의 깊이로 지반의 균질도를 확보하기 위해 Dry Pluviation 방법으로 조성되었다. 직경 35.7mm, 선단각도 60°의 표준 콘관입체가 모형 지반 정중앙에서 초속 2cm의 속도로 관입되었다. 본 연구에서는 Salgado(1993)에서 수행된 캘리브레이션 챔버 콘관입시험 중 모래의 밀도 및 상부압을 달리한 총 4가지 실험을 수치적으로 모사하였다. Table 1은 본 연구에서 모사한 캘리브레이션 챔버 콘관입시험을 나열한다.
Table 1. Experimental cases (Salgado 1993) numerically simulated in this study
| No. | Void ratio | Relative density (%) | Surcharge (kPa) | K0 |
| Case A | 0.78 | 52.6 | 50 | 0.47 |
| Case B | 0.78 | 52.6 | 100 | 0.47 |
| Case C | 0.67 | 81.6 | 50 | 0.43 |
| Case D | 0.67 | 81.6 | 100 | 0.43 |
Toyoura 모래는 최대 간극비 emax = 0.98, 최소 간극비 emin = 0.60, 균등 계수 Cu = 1.3, 평균 입경 D50 = 0.19 mm인 입도가 균등한 모래이다. Woo et al.(2017)은 한계상태 MC 모델을 이용하여 Toyoura 모래의 역학적 거동을 모사하기 위해 Dafalias et al.(2004), Dafalias and Manzari(2004), Gomes et al.(2016), Kim and Choo(2006), Li(2002), Li et al.(1999), Li and Dafalias(2000, 2002), Verdugo and Ishihara(1996), Vucetic(1994)의 연구를 참조하여 모델 매개변수 Cg, α, γtv, ν, , Γcs, λ, ξ, d0의 캘리브레이션을 수행하였다. Table 2는 산정된 모델 매개변수와 연관된 방정식 및 참조한 기존 연구를 나열한다.
Table 2. Model parameters for Toyoura sand
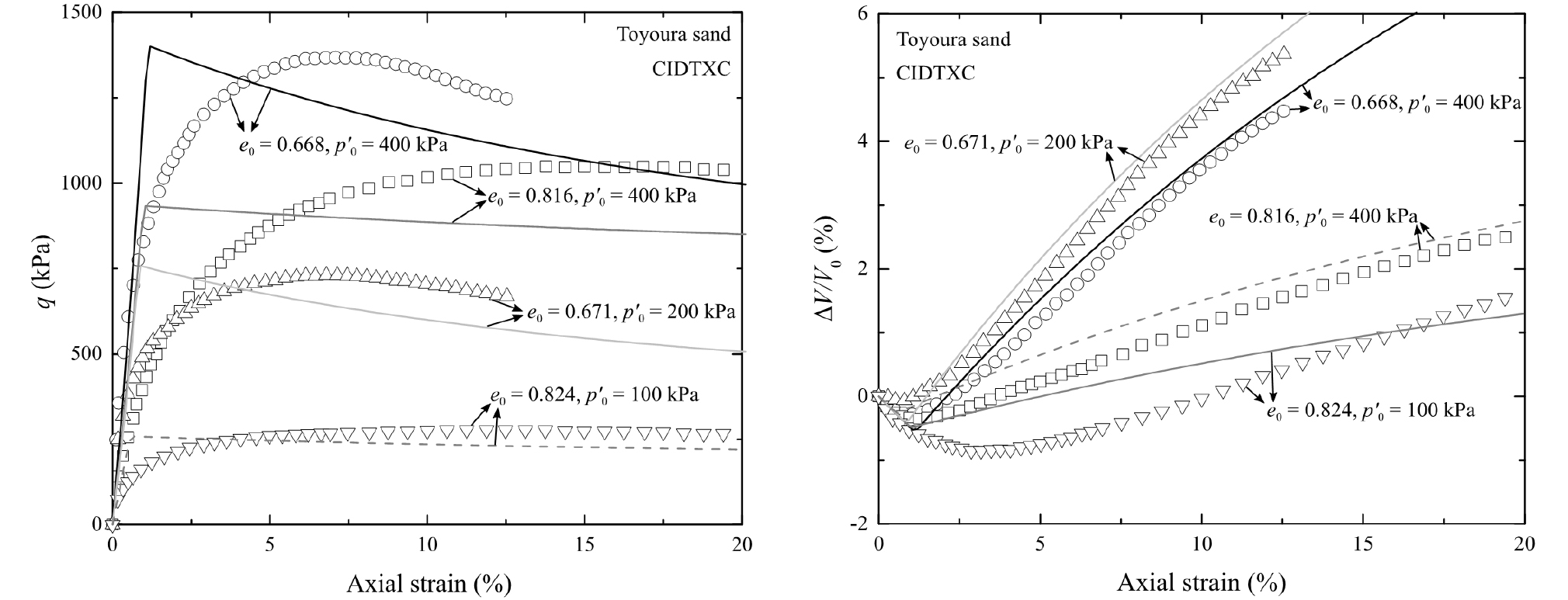
구성 모델이 모래의 역학적 거동을 알맞게 표현하기 위해서는 첨두값, 한계상태로의 진입, Dilatancy 현상을 수치적으로 모사할 수 있어야 한다. 이를 위하여 본 연구에서는 Toyoura 모래에 대해서 수행된 삼축압축시험을 한계상태 MC 모델을 이용하여 수치적으로 모사하였다. Fig. 1은 Fukushima and Tatsuoka(1984)에 의해 수행된 다양한 간극비와 초기 응력 상태인 Toyoura 모래에 대해서 수행된 등방압밀 배수 삼축압축시험 결과와 한계상태 MC모델을 이용한 수치해석 결과를 비교해서 보여준다. Fig. 1의 좌측 그림은 축방향 변형률(Axial Strain)에 대한 Von Mises 응력 q(= (3/2s:s)1/2, 삼축조건에서는 축차응력과 동일)의 변화를 보여준다. 비록 응력-변형률 곡선에서 첨두값에 도달하는 변형률은 차이가 나지만, 한계상태 MC모델은 첨두값의 크기는 유사하게 예측할 수 있다. 축방향 변형률에 대한 부피 변형률 변화(Fig. 1 우측 그림)을 보면, 한계상태 MC모델은 다양한 초기조건의 Toyoura 모래에 대해 전단에 따른 부피변형, 즉 Dilatancy 현상을 실험값과 매우 유사하게 모사할 수 있음을 알 수 있다.
3.2 콘관입체와 모래사이의 마찰
콘관입시험의 수치적 모사를 위해서는 관입체 표면과 모래와의 마찰을 고려하여야 한다. Ho et al.(2011), Kishida and Uesugi(1987), Uesugi and Kishida(1986)에 따르면, 모래와 강철(Steel) 사이의 마찰은 모래의 종류와 밀도 및 강철의 표면 거칠기(Surface Roughness)에 따라서 결정된다. Kishida and Uesugi(1987)에 따르면, 표면 거칠기가 2.4μm인 강판과 Toyoura 모래와의 마찰계수는 0.12로 측정되었다. Shmertmann(1978)에 따르면, 콘관입체는 스테인리스강으로 만들어져야 하며, 표면 거칠기는 0.5μm로 유지관리 되어야 한다. 이로부터, 콘관입체와 Toyoura 모래사이의 마찰계수는 0.12 보다 작음을 추정할 수 있다. 스테인리스강의 표면 거칠기가 0일 때, 모래와의 마찰계수를 0으로 가정하고, 선형 보간을 수행하면, 콘관입체와 Toyoura 모래 사이의 대응하는 마찰계수는 0.025이다. 이러한 조사를 바탕으로 본 논문에서는 Toyoura 모래와 콘관입체 표면 간의 마찰계수(μ)를 0, 0.02, 0.04, 0.06, 0.08로 조절하면서 수치해석을 수행하였다.
3.3 형상 및 격자의 구성
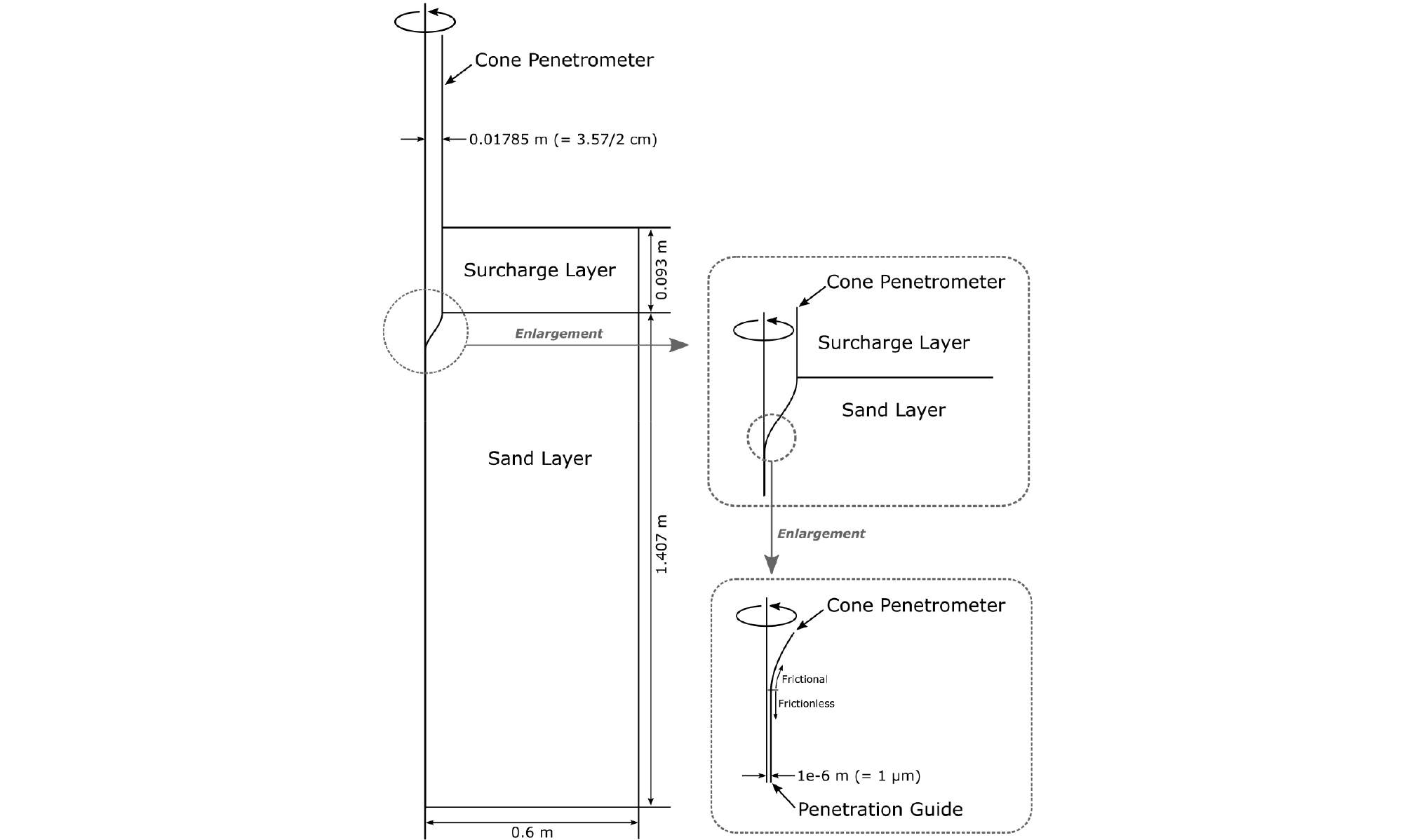
본 연구에서는 ABAQUS Explicit를 사용하여 유한요소 해석을 수행하였다. Fig. 2는 수치적 효율성을 위해 축대칭(Asymmetry) 조건을 적용한 지반과 관입체의 형상을 보여준다. Fig. 2에서 지반은 모래층과 하중 재하층(Surcharge Layer)으로 구분된다. 전체 지반에 대해서 중력은 연직 아래 방향으로 작용하며 중력 가속도는 9.81m/s2으로 설정하였다. 모래층은 한계상태 MC 모델을 따르는 Toyoura 모래로 구성하였으며, 하중 재하층은 선형탄성 재료로 가정하고, 탄성계수(Young’s Modulus) 100,000kPa, 포아송비 0.25로 설정하였다. 본 연구에서는 Table 1의 각 실험 조건에서 적용된 상부 하중을 하중 재하층의 단위중량을 조절하여 수치적으로 모사하였다.
축대칭 조건으로 유한요소 해석을 통해 깊은 관입을 수행할 경우, 대칭축에 존재하는 절점은 경계 조건상 축에서 분리될 수 없으므로, 격자의 왜곡이 심하게 발생하며 해석이 에러와 함께 종료되게 된다. 비록, Adaptive Meshing(Kardani et al., 2012; Nazem et al., 2006, 2012; Susila and Hryciw, 2003; Yu et al., 2008)와 Arbitrary Lagrangian Eulerian(ALE)(Nazem et al., 2008; Sabetamal et al., 2014; Sheng et al., 2009; Vavourakis et al., 2013) 기법 등을 활용하여 이러한 문제를 해결할 수 있지만, 적용법이 매우 복잡하고, 또한, 유한요소 해석 시 많은 추가 연산을 요구한다. 콘과 같이 선단부가 경사진 관입체의 관입시 지반 내부에 파괴면이 생성되기 보다는 관입체와 흙 경계에 파괴면이 생성되며, 지반이 아래쪽으로 압축되기 보다는 횡방향으로 압축되는 경향성이 보이는 특성을 보인다. 이러한 관찰을 바탕으로 Hügel et al.(2008)은 경사진 관입체의 관입을 일반(혹은 Lagrangian) 유한요소법을 이용하여 모사하기 위하여 관입 유도체 개념을 제안하였다. 본 연구에서는 Hügel et al.(2008)을 따라 관입 유도체를 이용하여 콘관입시험을 유한요소법을 이용하여 수치적으로 모사하였다.
콘관입체는 지반에 비해 강성이 매우 크므로, 강체로 가정하였으며, 이는 Fig. 2와 같은 축대칭 조건에서는 곡선으로 나타내어 진다. 전체 관입체는 콘관입체(Fig. 2의 Cone Penetrometer)와 관입 유도체(Fig. 2의 Penetration Guide)으로 구분된다. Fig. 2와 같이 콘의 모서리는 수치적 안정성을 확보하기 위해서 곡률반경을 1cm로 둥글게 처리했으며, 콘과 모래 지반사이는 마찰을 허용하고, 하중재하층 사이는 무마찰로 설정하였다. 관입 유도체는 콘관입체 하단에 부착되어 있으며, 대칭 축으로부터 횡방향으로 매우 작은 거리(1e-06m = 1μm)만큼 떨어져 있으며, 관입 유도체와 모래 지반 사이는 마찰저항이 없도록 설정하였다. 따라서 본 수치해석에서는 대칭축에는 절점이 존재하지 않으며, 콘의 관입에 따라 대칭축 근처에 모래 지반에 해당되는 절점이 자연스럽게 횡방향으로 이동할 수 있도록 하였다.
4. 해석 결과
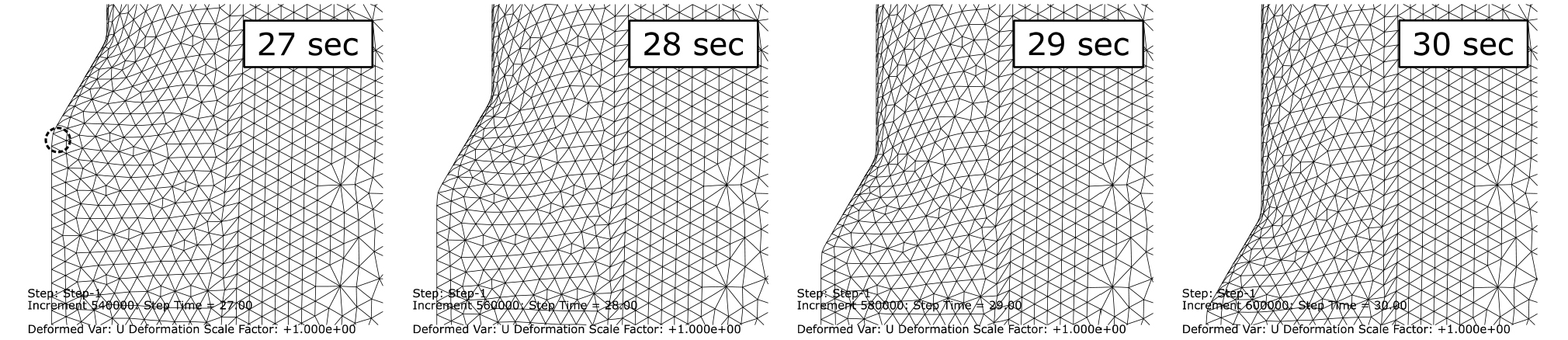
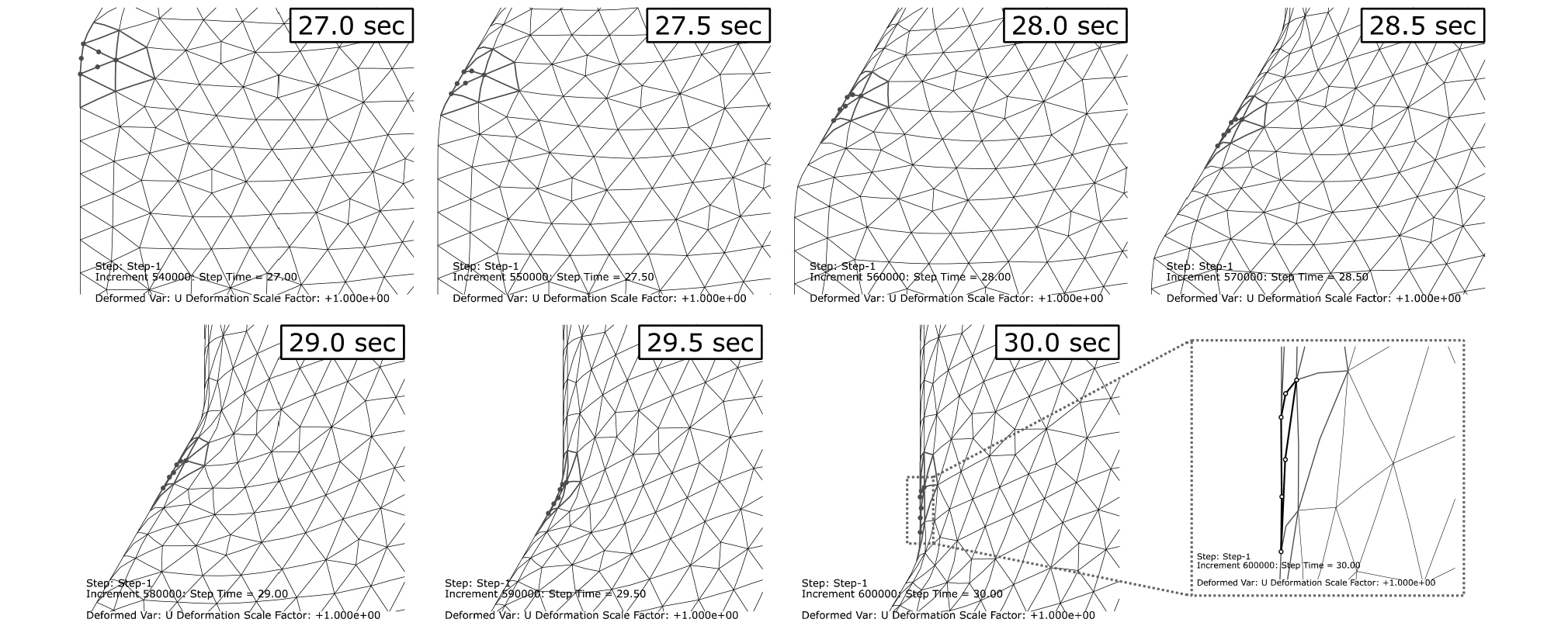
Fig. 3은 Case B 조건에서 콘과 모래사이의 마찰계수를 0.04로 설정했을 경우, 관입 27, 28, 29, 30 초 경과 후, 콘 선단부 근처 유한요소 격자의 변형을 보여준다. Fig. 3과 같이 관입 유도체의 활용에 따라서, 대칭축 근처의 요소가 찢어지지 않고 횡방향으로 자연스럽게 이동하여, 에러없이 콘의 관입이 수치적으로 진행됨을 알 수 있다. 유한요소 해석에서 과도한 변형은 요소의 왜곡을 일으키며, 요소의 왜곡은 가우스 적분의 정확도를 떨어뜨린다. 또한, 과도한 변형으로 인해 요소가 뒤집힐 경우, 요소의 면적이 음수로 산정된다. 이러한 이유로 유한요소법을 이용하여 대변위 문제를 모사할 경우에는, 자주 에러와 함께 해석이 종료되게 된다. 따라서, 본 연구에서는 깊은 관입시 근입체 부근 요소의 변형을 자세히 확인하였다. Fig. 4는 Fig. 3에서 회색 점선 원안의 요소의 관입 27, 27.5, 28, 28.5, 29, 29.5, 30 초 경과 후, 자세한 변형 양상을 보여준다. 대칭축 바로 옆에 위치한 요소는 콘 선단이 지나기 전에는 거의 변형이 발생하지 않는다. 선단이 요소를 지난 후에는 횡방향 이동, 횡방향 압축, 연직방향 인장이 발생하며, 또한, 콘관입체 표면을 따라서 전단변형이 발생하게 된다. 콘관입체가 지나간 이후, Fig. 4의 표시된 요소의 형상을 보면, 요소가 뒤집히지 않는 것을 확인할 수 있다. 또한 이 요소의 길이비는 대략 0.125로 ABAQUS의 요소의 왜곡에 대한 기본 기준값인 0.1보다 크다. 따라서, 본 연구에서 수행한 수치해석에서 해석을 종료시키거나, 결과에 영향을 줄 정도의 요소의 왜곡은 발생하지 않았다고 볼 수 있다.
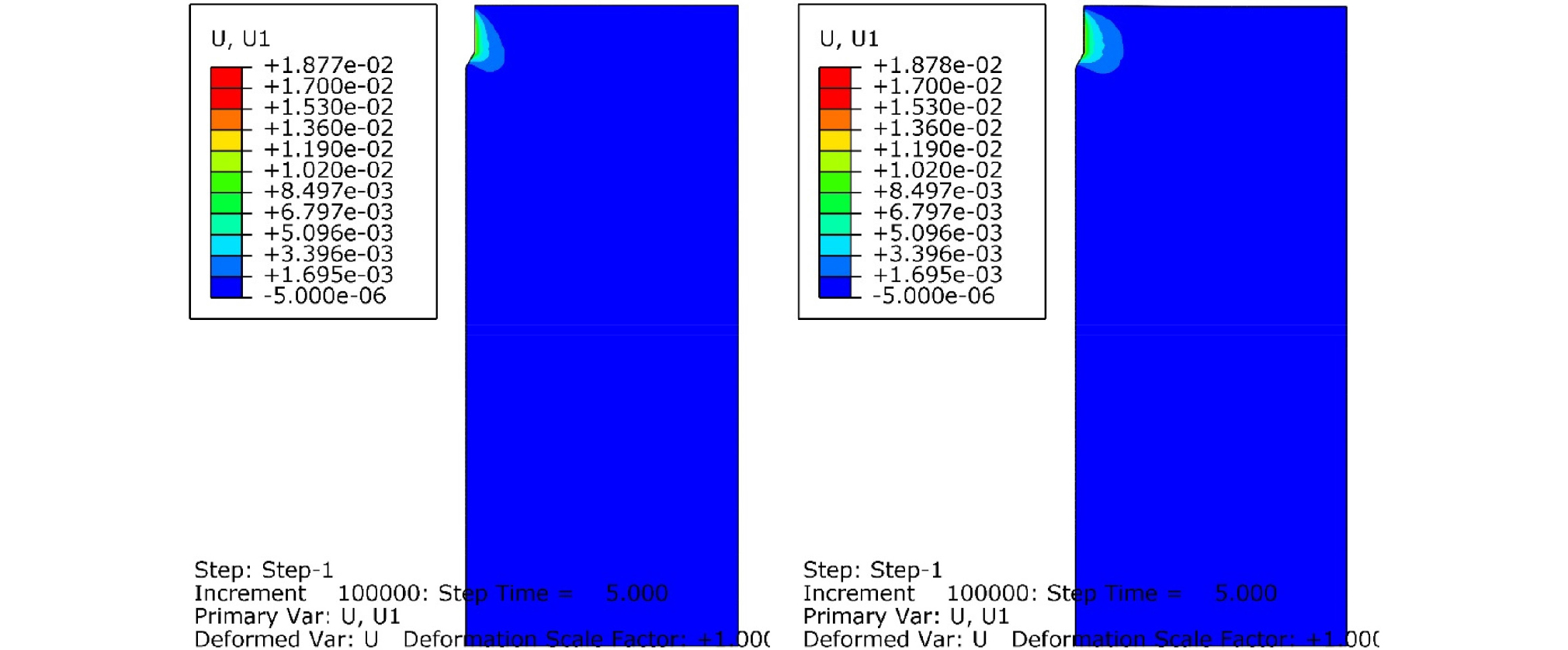
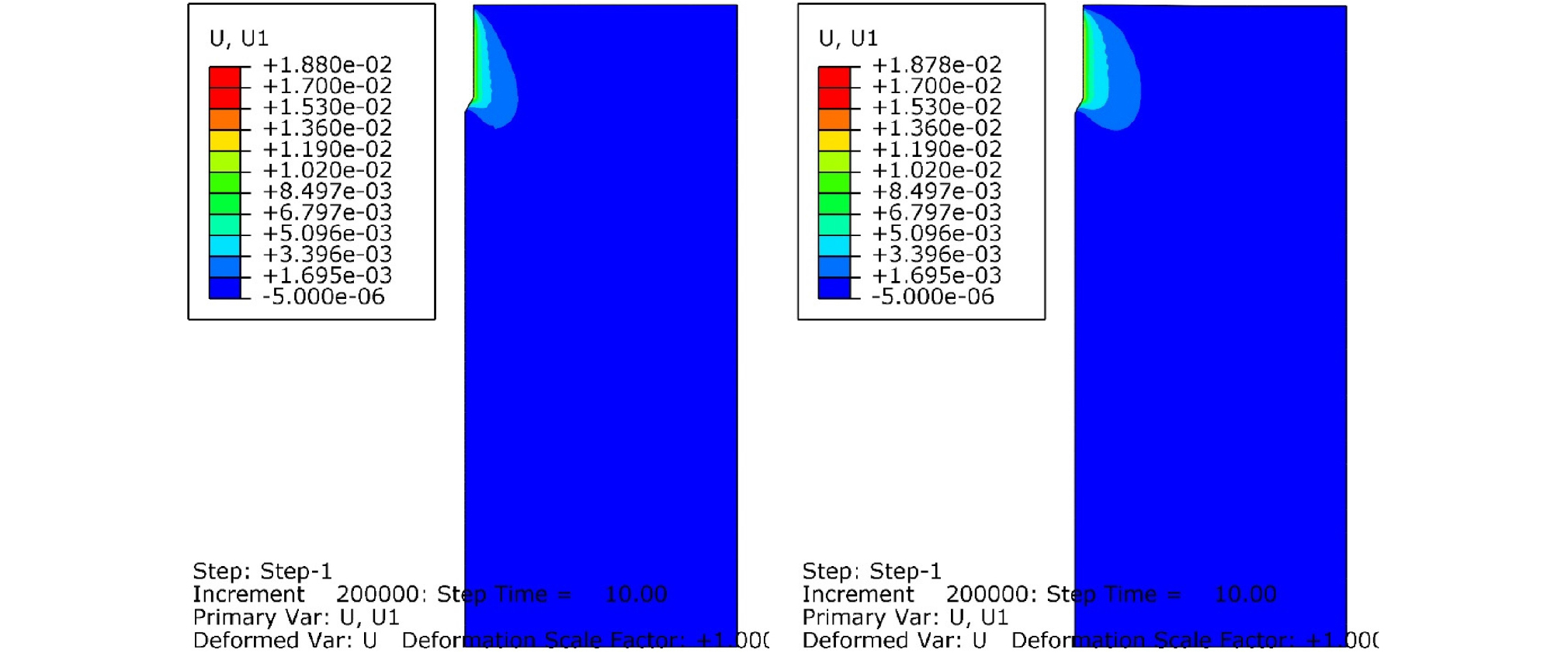
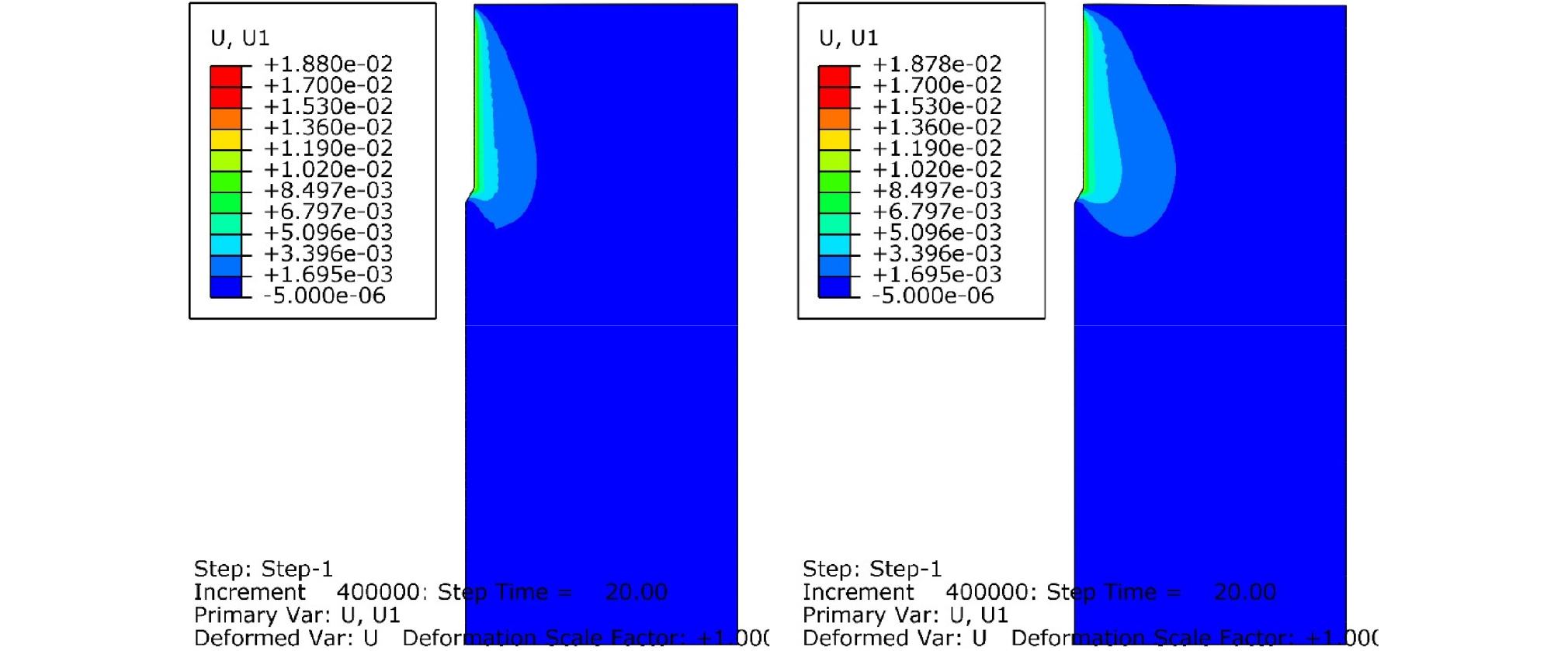
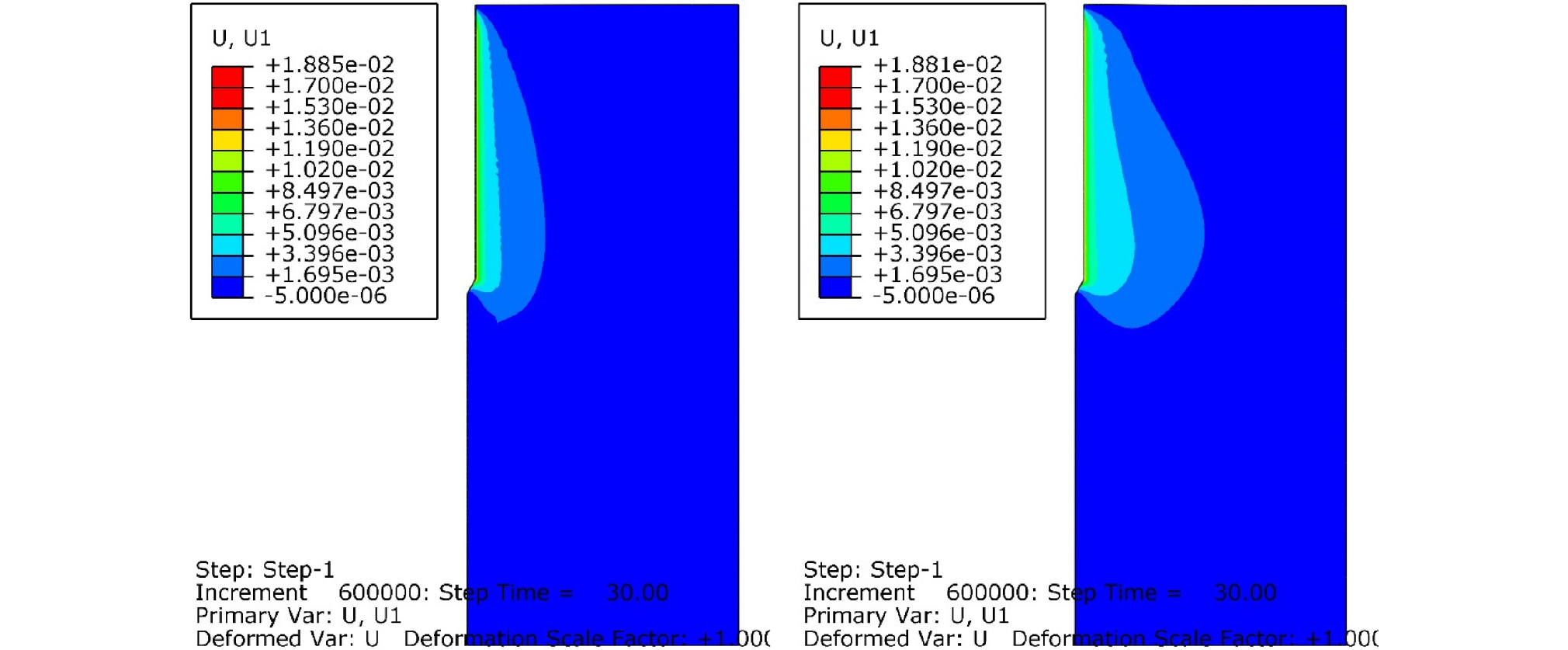
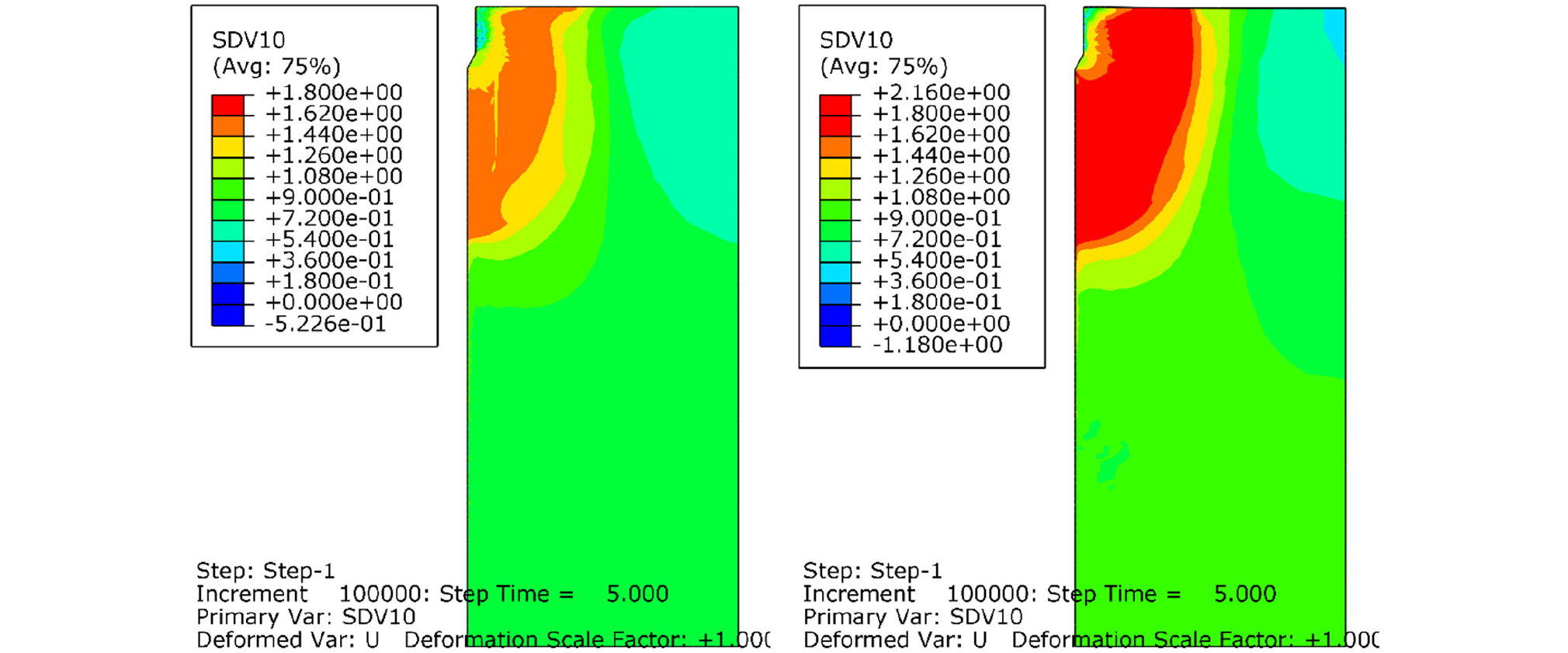
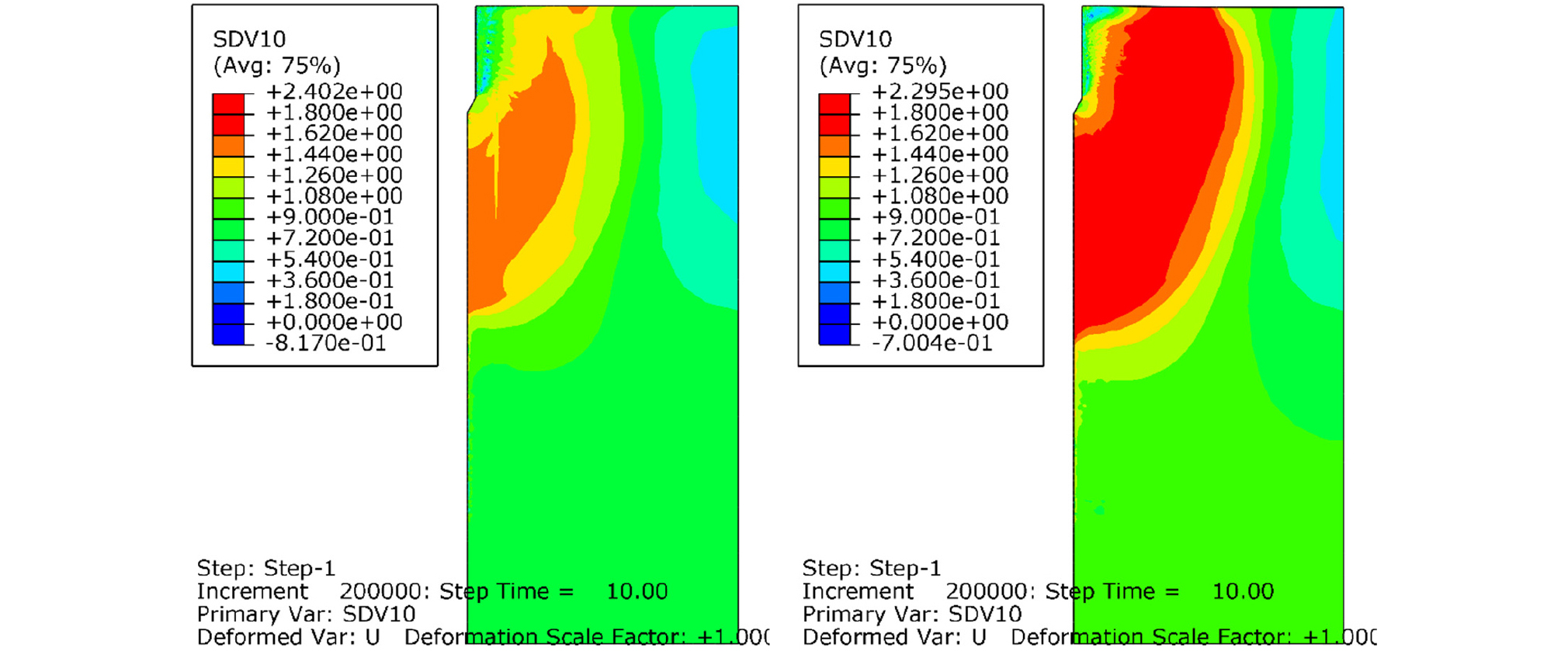
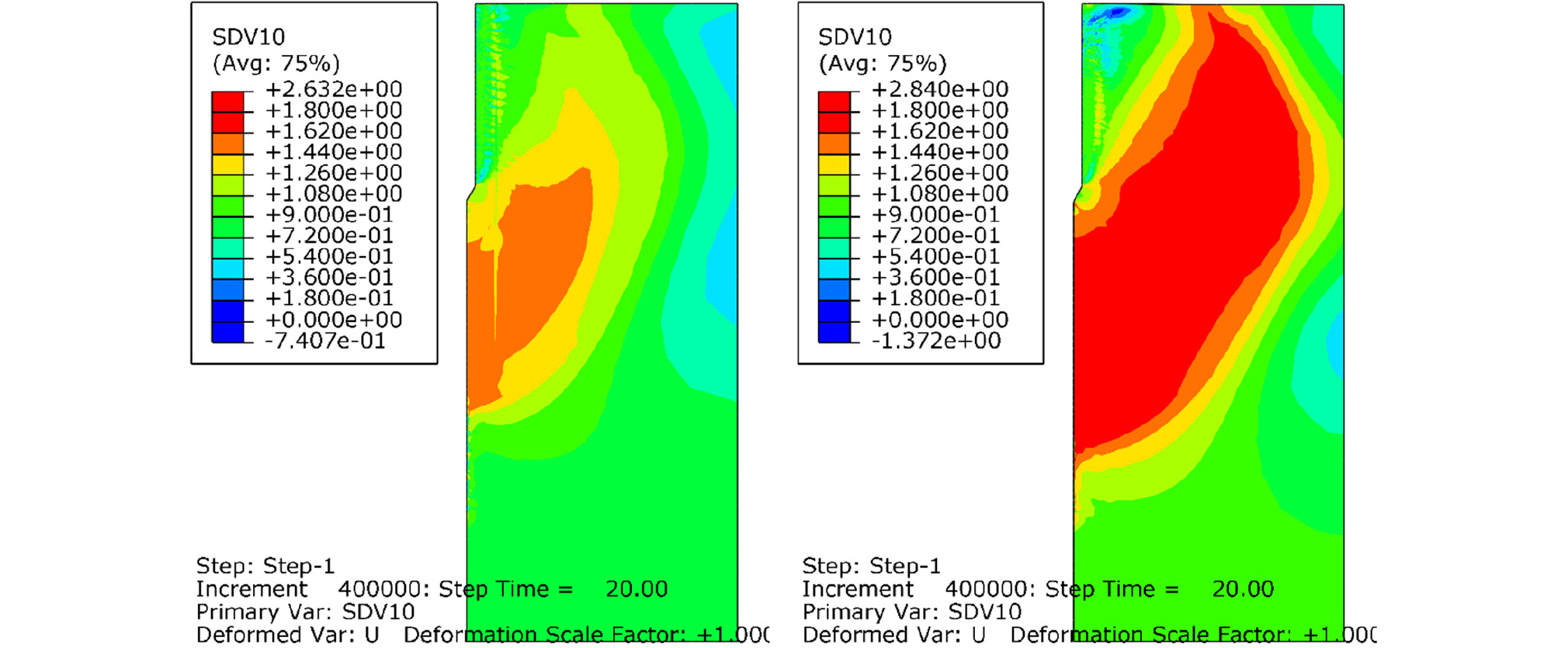
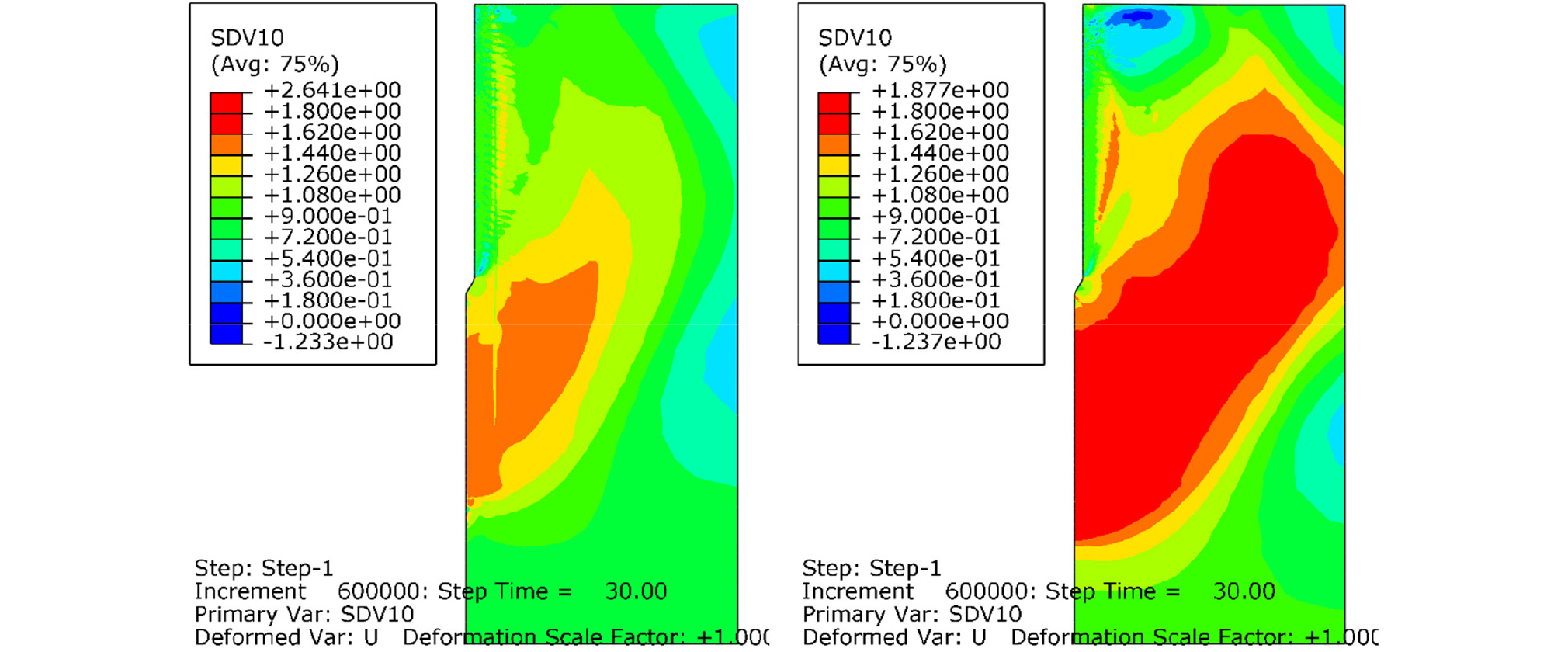
Fig. 5, 6, 7, 8은 각각 관입시간 5, 10, 20, 30초 경과 후, 콘과 모래사이의 마찰계수를 0.04로 설정했을 경우, Case A(좌측)와 Case C(우측)에 대해서 모래지반 내부의 횡방향 변위의 분포를 보여준다. Case A와 Case C 두 경우 모두, 연직 상재압은 50kPa로 동일하다. 하지만, Case A에서 모래지반의 상대밀도는 52.6%인 반면, Case C에서 모래지반의 상대밀도는 81.6%이다. 따라서 Fig. 5~12에서 Case A는 중간 조밀도의 모래를 대변하며, Case C는 조밀한 모래를 대변한다. Fig. 5, 6, 7, 8에서 콘의 관입시, 선단부보다 낮은 위치에 있는 지반에서는 횡방향 변위가 거의 발생하지 않았다. 관입이 진행될 수록, 횡방향 변위가 발생하는 영역이 횡방향으로 점점 팽창한다. 이 횡방향 변위의 횡방향 영향 범위는 모래 지반이 조밀할수록 커지는 것을 확인할 수 있었다. 관입 30초 이후에는 횡방향 변위의 횡방향 영향 범위는 더 이상 커지지 않았다. 최종적으로 콘 관입체 반경의 약 10%의 횡방향 변위가 발생하는 영역은 Case A(중간 조밀도의 모래 지반)에서 대칭축으로부터 콘 반경 rc의 약 4배 정도 되며, Case C(조밀한 모래 지반)에서는 대칭축으로부터 약 6rc 정도였다. 이는 조밀한 모래일 수록, Dilatancy 현상이 크게 발생하고, 모래가 전단변형시 더욱 팽창하여, 주변 모래를 횡방향으로 밀어내기 때문이다.
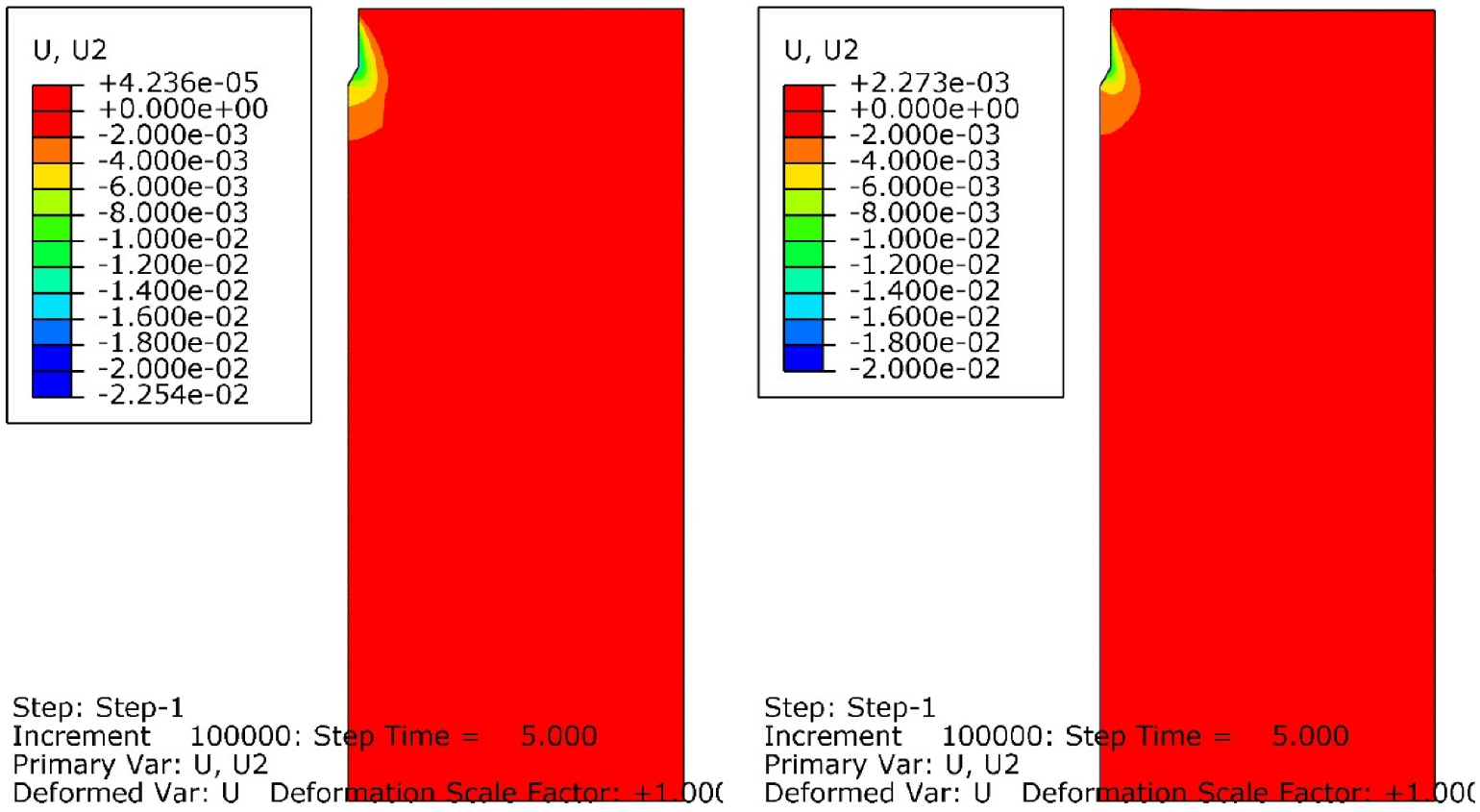
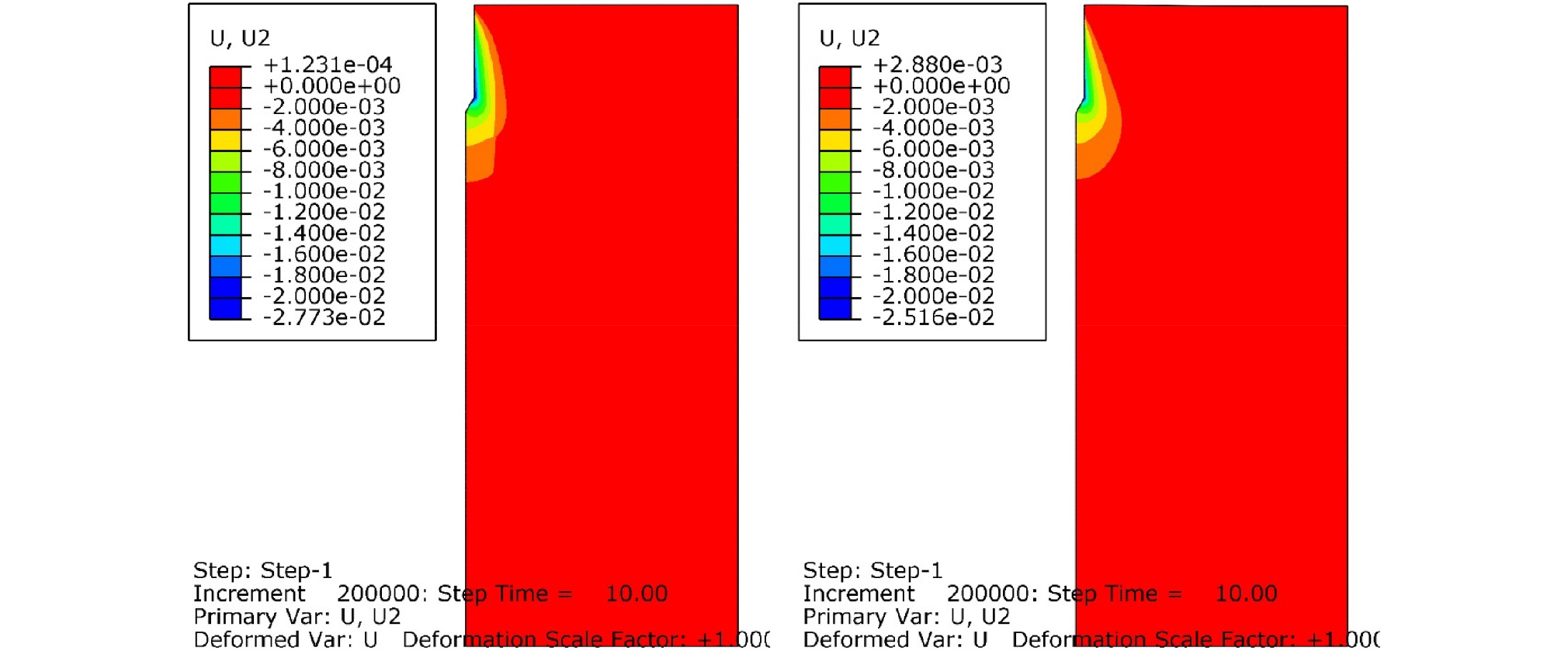
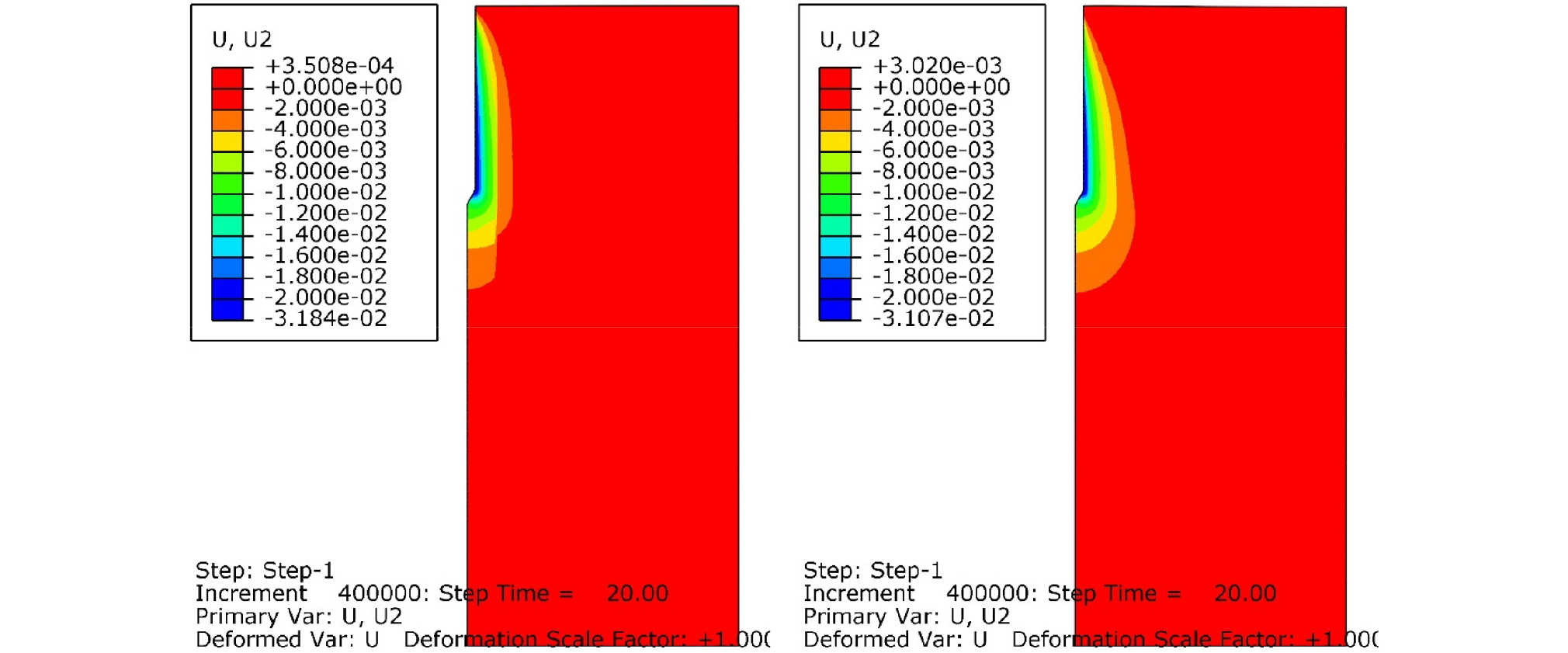
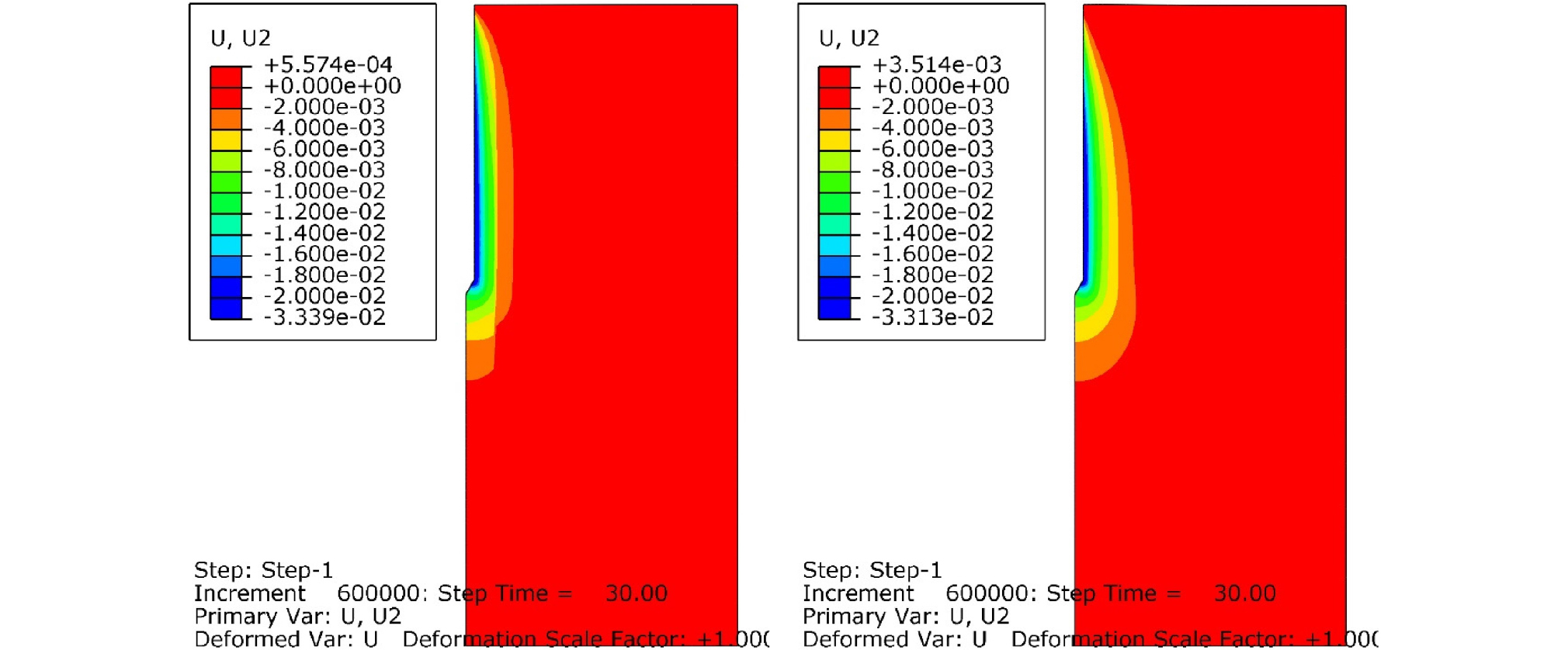
Fig. 9, 10, 11, 12는 각각 관입시간 5, 10, 20, 30초 경과 후, 콘과 모래사이의 마찰계수를 0.04로 설정했을 경우, Case A(좌측)와 Case C(우측)에 대해서 모래지반 내부의 연직방향 변위의 분포를 보여준다. 관입 시간 5, 10, 20, 30초 경과후에 콘의 관입 깊이(zp)는 각각 10, 20, 40, 60cm이다. Fig. 9, 10, 11, 12에서 보이는 관입 깊이 10, 20, 40, 60cm 일 때, 모래 지반에 발생한 최대 연직방향 변위를 보면, 연직 하방으로 Case A에서는 2.25, 2.77, 3.18, 3.34cm 그리고 Case C에서는 2.00, 2.52, 3.11, 3.31cm으로 나타나, 30 초 관입 경과 후, 지반의 최대 연직 방향 변위는 콘의 관입 깊이의 대략 5%로 매우 작음을 알 수 있다. 이는 경사진 표면을 가진 관입체의 관입시, 모래 지반이 연직방향으로 계속 이동 및 압축되기 보다는 횡방향으로 이동 및 압축되기 때문이다. 관입이 진행될 수록, 연직방향 변위가 발생하는 범위는 횡방향으로 점점 늘어났으며, 이 연직방향 변위의 횡방향 영향 범위는 모래 지반이 조밀할수록 커지는 것을 확인할 수 있다. 최종적으로 콘 관입체 반경의 약 10%의 연직방향 변위가 발생하는 횡방향 영향 범위의 크기는 Case A에서 대칭축으로부터 3rc, Case C에서 대칭축으로부터 약 4rc로 측정되었다. 횡방향 변위와는 달리, 연직방향 변위는 콘 선단부 아래에서도 크게 발생한다. 콘 관입체 반경의 약 10%의 연직방향 변위가 발생하는 연직방향 영향 범위는 Case A, C 모두 대략 콘 선단부 아래 6rc까지로 수치해석 결과 측정되었다.
Fig. 13, 14, 15, 16은 각각 관입시간 5, 10, 20, 30초 경과 후, 마찰계수 μ = 0.04 일 때, Case A(좌측)와 Case C(우측)에 대해서 모래지반 내부의 응력비 M (= q/p')의 분포를 보여준다. 삼축 압축 및 인장 조건에서 한계상태 마찰각과 응력비 사이의 관계는 다음과 같다.
| $$M_{cc}=\frac{6\;\sin\phi_{cs}}{3-\sin\phi_{cs}},\;M_{ce}=\frac{6\;\sin\phi_{cs}}{3+\sin\phi_{cs}}$$ | (12) |
여기서 Mcc는 삼축 압축 조건에서의 한계상태 응력비, Mce는 삼축 인장 조건에서의 한계상태 응력비이다. 식 (12)에 Toyoura 모래의 한계상태 마찰각 31.84°을 대입하면, Mcc = 1.28, Mce = 0.90이 된다. 따라서 그림 Fig. 13, 14, 15, 16에서 변형이 크게 발생한 구역에서 응력비가 0.90~1.28 사이에 있다면, 모래는 대략적으로 한계상태에 있을 것이라 가정할 수 있다. 만일 응력비가 1.28보다 크다면, 현재 응력상태는 한계상태 이전 첨두값 부근에 있다고 생각할 수 있다. Fig. 13, 14, 15, 16에서 변형이 크게 발생한 선단부 부근 모래는 한계상태에 진입하였음을 알 수 있다. 선단부 바깥쪽으로는 응력비가 한계상태보다 큰, 현재 응력-변형률 상태가 첨두값 근처에 있는 영역이 선단부 근처 한계상태 진입영역을 감싸고 있다. 이 첨두값 영역의 크기는 모래가 조밀할수록 크다. 이는 조밀한 모래일수록 Dilatancy 현상이 커서 모래가 더욱 팽창하고, 모래가 팽창할수록 더욱 넓은 영역으로 하중이 전이되기 때문이다. 첨두값 영역의 크기는 관입 초기(Fig. 13, 14, 15)에는 계속 증가하다가 그 이후에는(Fig. 15, 16) 더 이상 크기가 증가하지 않고 콘관입체를 따라 아래로 이동한다. 또한, 첨두값 응력비의 절대값의 크기도 모래가 조밀할수록 크며, 이는 모래가 조밀할수록 식 (11), (12)에 의해 첨두값 응력비가 커지기 때문이다.
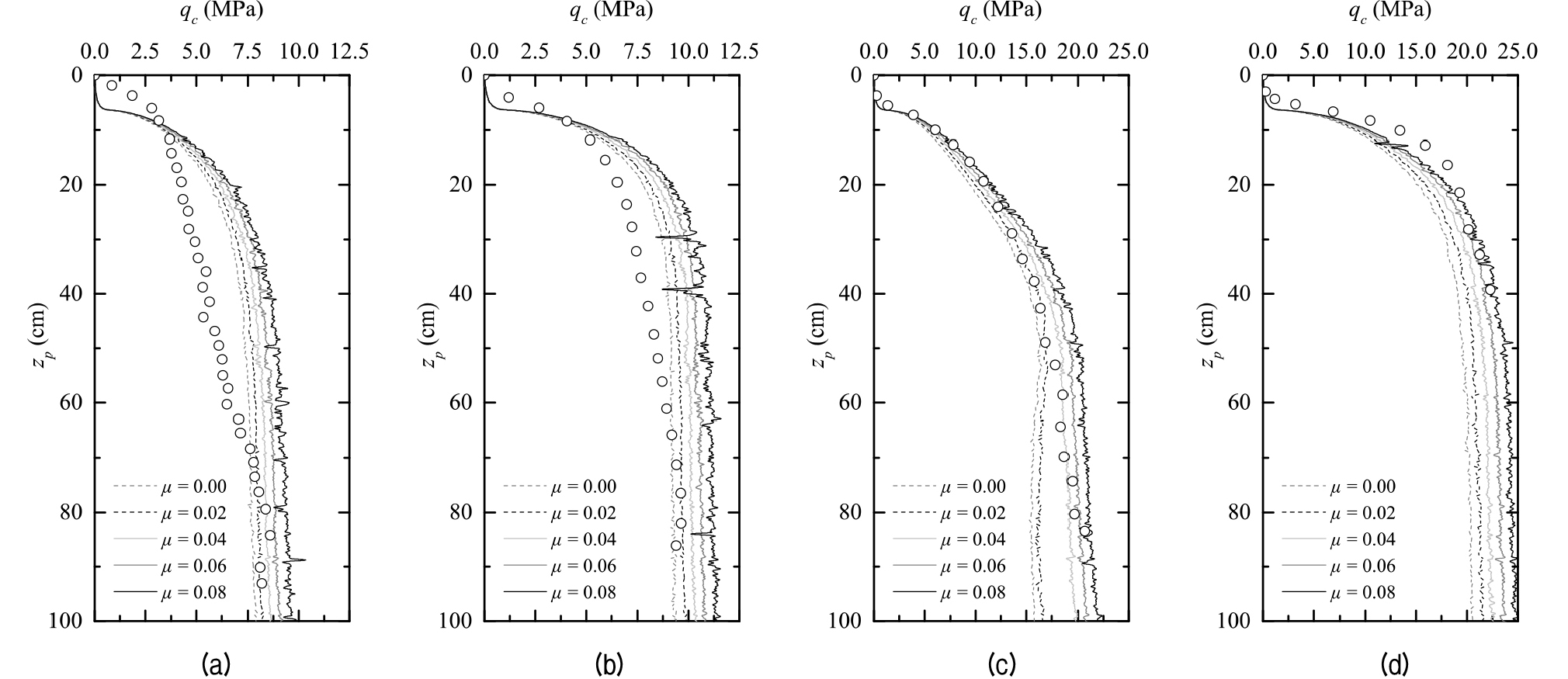
Fig. 17은 Table 1의 모든 경우에 대해서 관입 깊이 zp에 대한 콘 관입 저항력 qc의 반응을 보여준다. 여기서 선은 콘관입체와 모래 지반사이의 마찰계수 μ를 0, 0.02, 0.04, 0.06, 0.08로 조절하면서 수행한 수치해석 결과이며, 원형 심볼은 Salgado(1993)에 의해 수행된 실험 결과이다. 수치해석 결과 모든 해석 조건에서 마찰계수를 0.02 증가시킬 경우, 선단 저항력이 대략 5% 정도 증가함을 알 수 있었다. Salgado(1993)에 의해 수행된 실내 실험 결과와 비교해보면, 중간 조밀도의 모래 지반의 경우(Case A, B), 비록 수치해석이 관입 초기의 콘 관입 저항력을 실험 결과보다 과대 평가 하지만, 최종적으로 도달하는 콘 관입 저항력은 수치해석이 실험값을 유사하게 예측함을 알 수 있다. 조밀한 모래 지반의 경우(Case C, D), 한계상태 MC 모델을 이용한 유한요소 해석이 실험값을 매우 유사하게 모사할 수 있음을 알 수 있다.
5. 요약 및 결론
본 논문은 한계상태 이론을 기반으로 수정한 Mohr Coulomb (MC) 모델을 활용하여 모래의 역학적 거동을 모사하여, 축대칭 조건하에서 콘 관입 시험을 유한요소법을 이용하여 수치적으로 해석하였다. 한계상태 MC 모델에서 팽창각은 간극비(e)-평균유효응력(p') 공간상에서 한계상태 간극비와 현재 간극비 사이의 연직거리의 함수로 표현된다. 한계상태 MC 모델을 활용하여 Toyoura 모래에 대해 수행된 배수 삼축 압축 시험을 수치 모사 해본 결과, 한계상태 MC 모델은 첨두값의 크기, 첨두값 이후 한계상태로의 연화거동, Dilatancy 현상을 모사할 수 있었다.
콘관입시험을 수치적으로 모사하기 위해서는 관입시 지반내에서 발생하는 대변위와 지반과 콘 관입체 간의 접촉을 고려해야 한다. 축대칭 조건을 이용해서 깊은 관입을 모사할 경우, 대칭축에 위치한 요소들은 왜곡되거나 찢어지게 된다. 이를 방지하기 위해, 경사진 관입체에 대해 적용가능한 관입 유도체를 적용하여, 선단부에 위치한 요소들이 자연스럽게 횡방향으로 밀리도록 하였다. 또한, 기존 연구들을 분석하며, 콘관입체와 Toyoura 모래 사이의 마찰계수를 0.00~0.08 사이로 추정하고 이를 적용하여 유한요소 해석을 실시하였다.
캘리브레이션 챔버에서 Toyoura 모래 지반에 대해 수행된 콘관입시험에 대해서 한계상태 MC 모델을 이용한 유한요소 해석을 수행하였다. 해석 결과, 조밀한 모래일수록 Dilatancy 현상이 크게 발생하여, 횡방향 및 연직방향 변위가 발생하는 영역의 크기가 컸다. 지반 내부의 응력비의 분포를 확인한 결과, 변형이 크게 발생하는 선단부 근처의 모래 지반은 한계상태에 진입하였고, 응력상태가 첨두값 부근에 있는 영역이 감싸고 있었다. 수치해석으로 구한 콘관입저항력 qc을 산정한 결과, 중간 조밀도의 모래에 대해서는 관입 초기에는 수치해석이 실험 결과에 비해 qc를 과대평가하지만, 최종적으로 도달하는 qc는 실험값과 유사함을 알 수 있었다. 조밀한 모래에 대해서는 수치해석은 실험에서 구한 관입심도 대비 qc를 잘 예측함을 알 수 있었다. 본 연구에서 제안한 한계상태 MC 모델과 근입 유도체 기법을 활용한 유한요소법을 활용하여 콘관입시험 결과에 미치는 주요 영향인자를 분석하여, 콘관입시험 결과와 주요 지반 정수 간의 상관관계 파악을 기대할 수 있다.